苗正伟1,徐利岗2
(1.河北水利电力学院 水利工程系,河北 沧州061001;2.宁夏水利科学研究院,银川750021)
摘 要:应用改进的FCM(Fuzzy C-Means,模糊C均值聚类)算法对承德市1951—2015年的年降水序列进行模糊聚类,获得10个聚类中心和隶属度矩阵。根据最大隶属原则确定每年的降水状态,采用规范化的各阶自相关系数为权重,建立了加权马尔可夫链模型。以隶属度向量作为预测时的初始状态向量,通过该模型逐年预测了承德市2004—2015年的降水状态,结果与实际情况一致。引入模糊集中的级别特征值公式,并对该公式做出修正。基于马尔可夫链的预测结果,应用修正后的级别特征值公式预测了2004—2015年的降水量,所有预测结果的相对误差都在7%以内,初步表明基于模糊聚类和加权马尔可夫链的降水预测模型是合理可行的。
关 键 词:预测;降水;模糊聚类;FCM算法;加权马尔可夫链;承德
用加权马尔可夫链进行降水预测的首要问题就是降水状态的划分,通常用均值-标准差法将降水序列分为5个状态,但这种方法没有考虑降水量的实际分布特征,仅从统计的角度将样本均值作为数据中心[1],这很容易破坏序列的数据结构。另外,该法划分的结果非此即彼,因此预测时的初始向量为单位向量,即初始时刻所处状态的概率是100%,而其他状态的概率都是0,这势必导致很多历史信息的丢失[2]。鉴于以上二点,应用改进的FCM算法对降水序列进行模糊聚类,并赋予每个年降水量属于各模糊聚类的隶属度,从而用隶属度向量作为初始向量进行预测。
传统的聚类划分是一种硬划分,其中对象具有非此即彼的性质,但现实中多数对象在性态和类属方面存在模糊性,适于软划分。Zadeh提出模糊集理论后,人们开始用模糊的方法来处理聚类问题,即模糊聚类分析[3]。其中,应用最广泛且较成功的是模糊C均值聚类,实现模糊C均值聚类的经典算法是FCM算法,该算法是把n个向量xt(t=1,2,…,n)分为c个模糊聚类,并求隶属度矩阵和各聚类中心,使目标函数达到最小[4]。FCM算法的目标函数定义为:
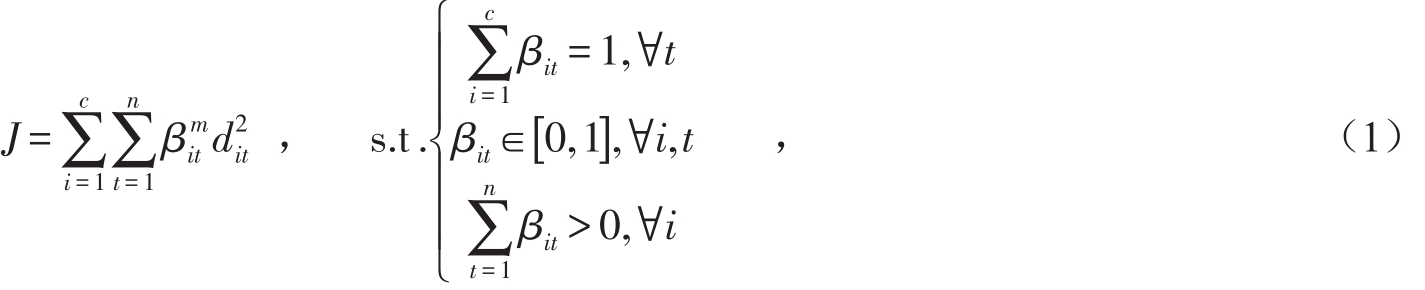
式中:βit为第t个数据对第i个模糊聚类的隶属度;dit=||θi-xt||为第i个聚类中心与第t个数据间的欧氏距离;θ为第i个聚类中心;m为模糊指数,控制隶属度在各类之间的权重[5]。
对式(1)应用拉格朗日乘数法[6]可得:

可见,FCM算法是一个简单的迭代过程,然而,由于算法的每一次迭代都是沿着使目标函数减小的方向进行的,而目标函数可能有多个极值点,若初始聚类中心选在一个局部极小点附近,就可能会使算法收敛到局部极小,即FCM算法对初始值敏感,而传统FCM算法的初始聚类中心是随机产生的,因此所得结果很不稳定[7][8],故采用文献[9]中的改进FCM算法进行模糊聚类,改进算法的基本步骤为:
1)设定类间最小距离阈值为α>0,计算任意2个样本间的距离,将其中距离最近的2个样本作为第一类,并将二者的均值作为第一个聚类中心;
2)找出与第一类2个样本的距离都大于α的所有样本,并在这些样本中选择距离最近的2个点定为一类,取其均值作为第二类聚类中心;
3)同理,在剩下的样本中找到与已经找到的样本的距离都大于α的所有样本,并选择这些样本中距离最近的2个点作为一类,并取二者均值为该类的聚类中心。
4)重复3),直到找到所有的聚类中心,并将之作为初始聚类中心。
5)由式(3)计算隶属度;
6)按式(4)修正所有的聚类中心;
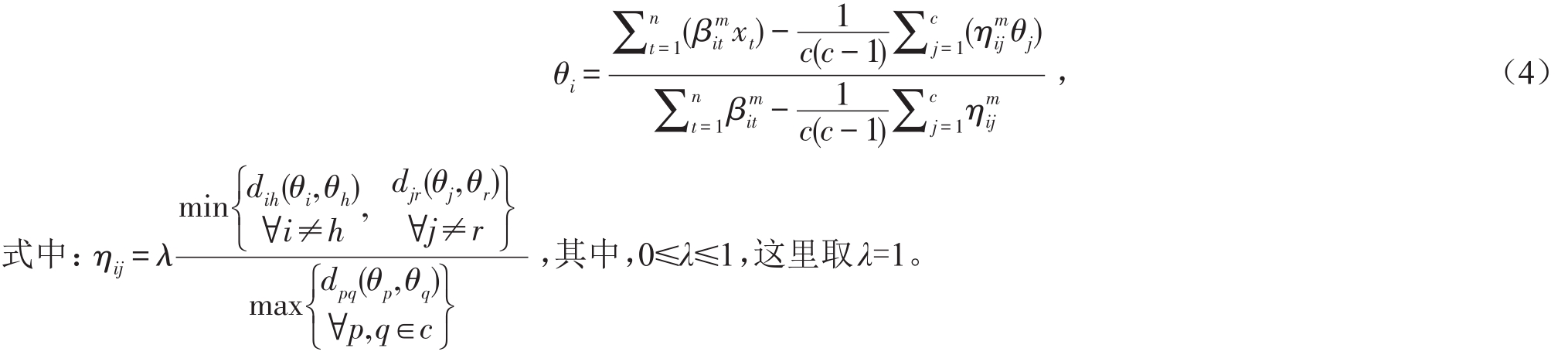
7)计算误差;
式中:k为迭代次数。若e小于给定的误差阈值,算法结束;否则,转步骤5)。
8)根据最大隶属原则将样本归类。
FCM算法需要人为给定聚类数,对每一个理论上可行的聚类数,该算法都能给出相应的聚类结果。当聚类数有多个可能时,哪一种聚类效果最好?这就是聚类有效性问题,即判定最优聚类数[10-13]。目前用于判定最优聚类数的指标有很多,由于适于降水序列的分类数的范围很有限,因此,本文选用经典的Xie-Beni有效性指标Vxie,其定义为:

对于给定范围内的每个聚类数,用式(6)计算Vxie,使Vxie达到最小值的即为最优聚类数。
马尔可夫链这种随机过程的基本特征是无后效性,然而自然界中的很多现象不能严格满足该特性,因此出现了加权马尔可夫链模型,其基本原理见参考文献[14]。
为计算具体预测值,引入级别特征值公式[15-16],首先计算状态i的权重wi,即:

式中:τ为状态个数;pi为状态i的预测概率;E为状态空间;η为最大概率作用系数。级别特征值H定义为:
降水量预测值xi为:

式中:Ui、Li分别为状态i所在区间的上下限。
1)确定最优聚类数。
2)应用改进的FCM算法进行模糊聚类,根据最大隶属原则,确定各年降水量的状态。
3)计算k步转移矩阵的权重ωk:
式中:rk为第k阶自相关系数;b为最大步长。
4)用转移频率近似代替转移概率[17],由此计算转移矩阵。
5)设待预测年份为t0,则距t0步长为k(k=1,2,…,b)的预测概率向量Tk由下式给出:
式中,t=t0−k;βt表示年份为t的隶属度向量;P(k)表示k步转移矩阵;ωk表示步长为k的权重。
6)将各步长的概率向量求和:
T向量中各元素的最大值所对应的状态即为预测状态。
7)应用级别特征值公式预测降水量具体值。
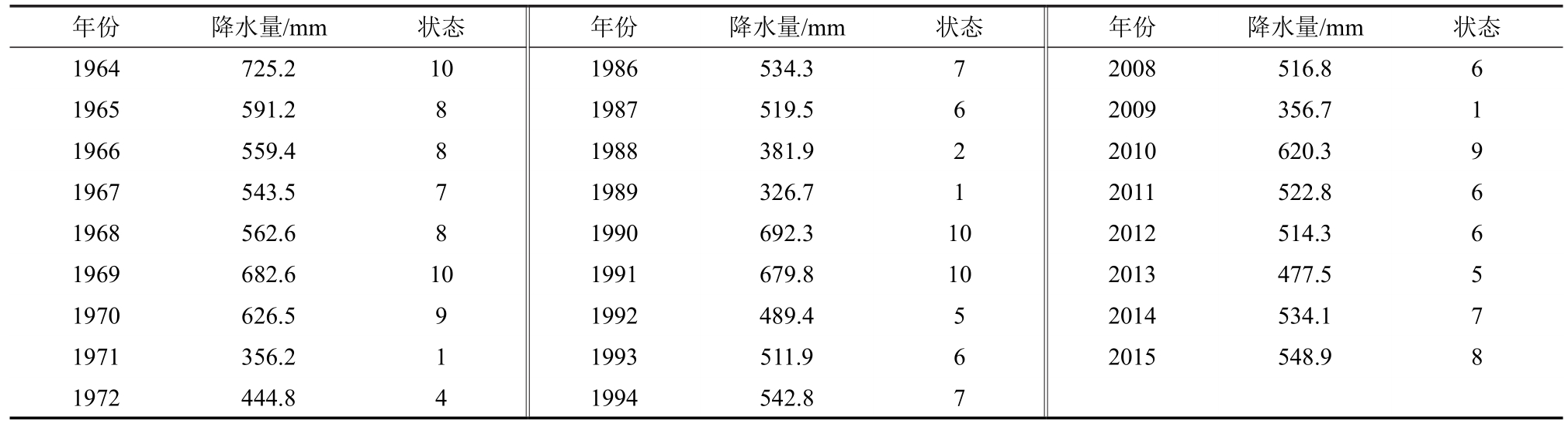
兹选用承德市1951—2015年的逐月降水量,并将之整理为年降水序列,资料源于“中国气象数据网”,如表1所示。
表1 承德市1951—2015年降水量及其状态
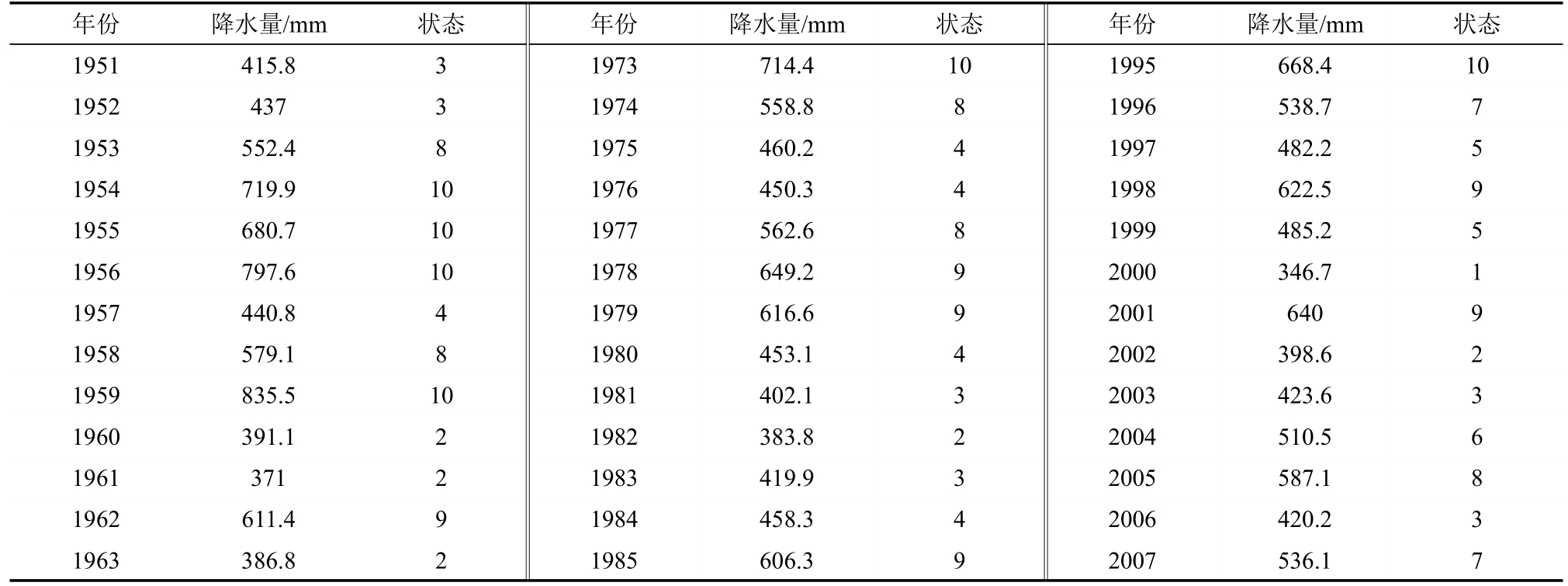
续表1
1)最小聚类数取2,最大聚类数取12,应用式(6)计算Vxie指标,结果见表2。
表2Vxie指标
由表2知,聚类数为10时指标值最小,因此最优聚类数为10。
2)根据改进的FCM算法原理,编制MATLAB程序进行计算,获得隶属度矩阵和10个聚类中心。对于隶属度矩阵,因数据量为10×65,限于篇幅,略。以隶属度的最大隶属原则确定各年降水量的状态,结果见表1;聚类中心及状态区间见表3。
表3 承德市1951—2015年降水量分类及聚类中心

3)最大步长及权重的确定:经试算确定最大步长为21,计算1~21阶的权重,结果如表4。
表4 1~21阶权重
4)对降水状态序列进行统计计算,得步长从1~21的转移概率矩阵,因篇幅限制,只列出P(1)和P(21)示意:

5)首先根据1983—2003年的年降水数据预测2004年的年降水状态。
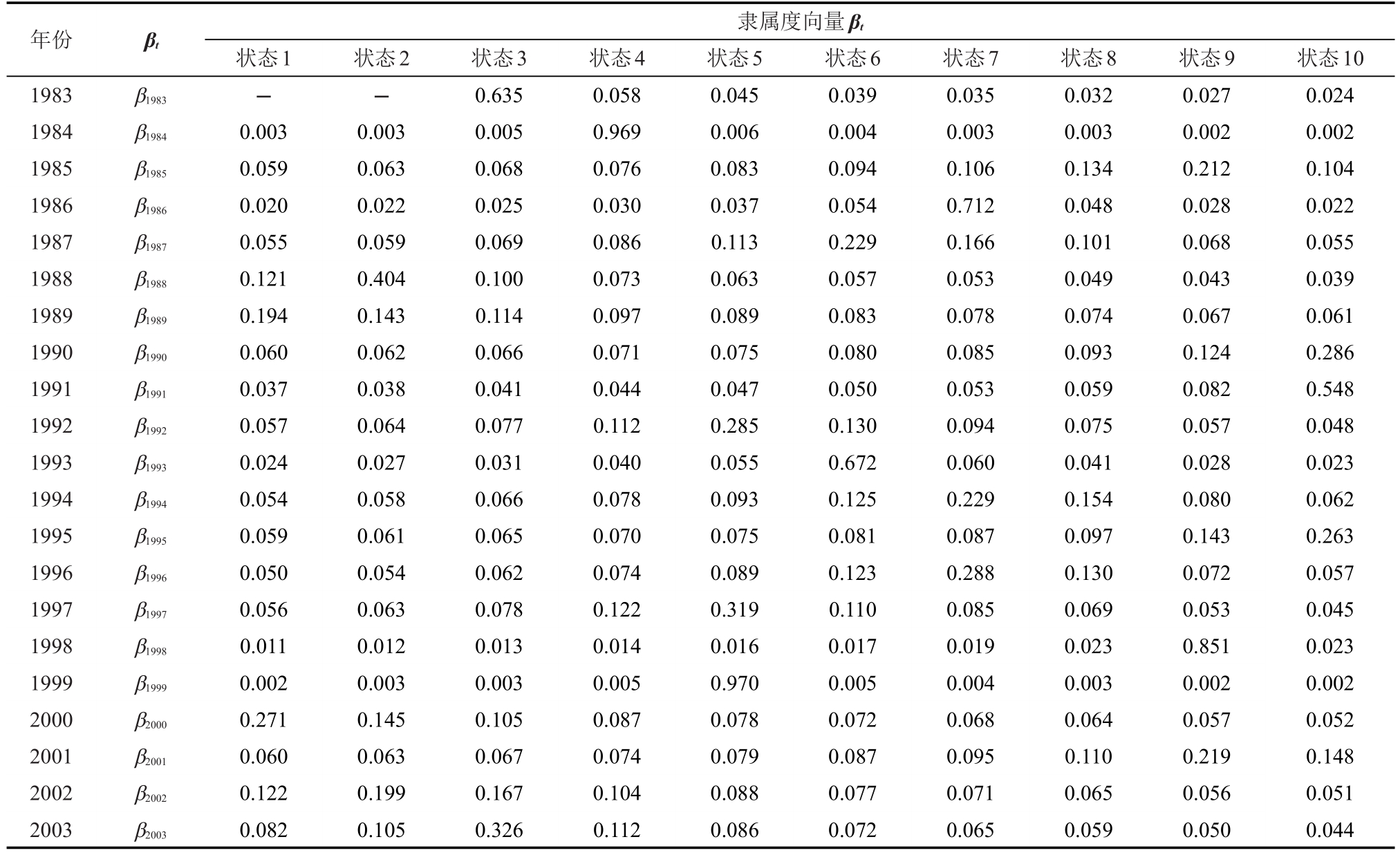
1983—2003年降水量的隶属度如表5。求解下列二式:

式中:Tk表示步长为k的转移矩阵的预测结果;βt表示年份为t的隶属度向量;P(k)表示k步转移矩阵;k=2004-t,t=2003,2002,…,1983。
表5 1983—2003年降水量隶属度
概率向量T中各元素的最大值对应的状态即为预测值,见表6。
表6 2004年降水状态预测
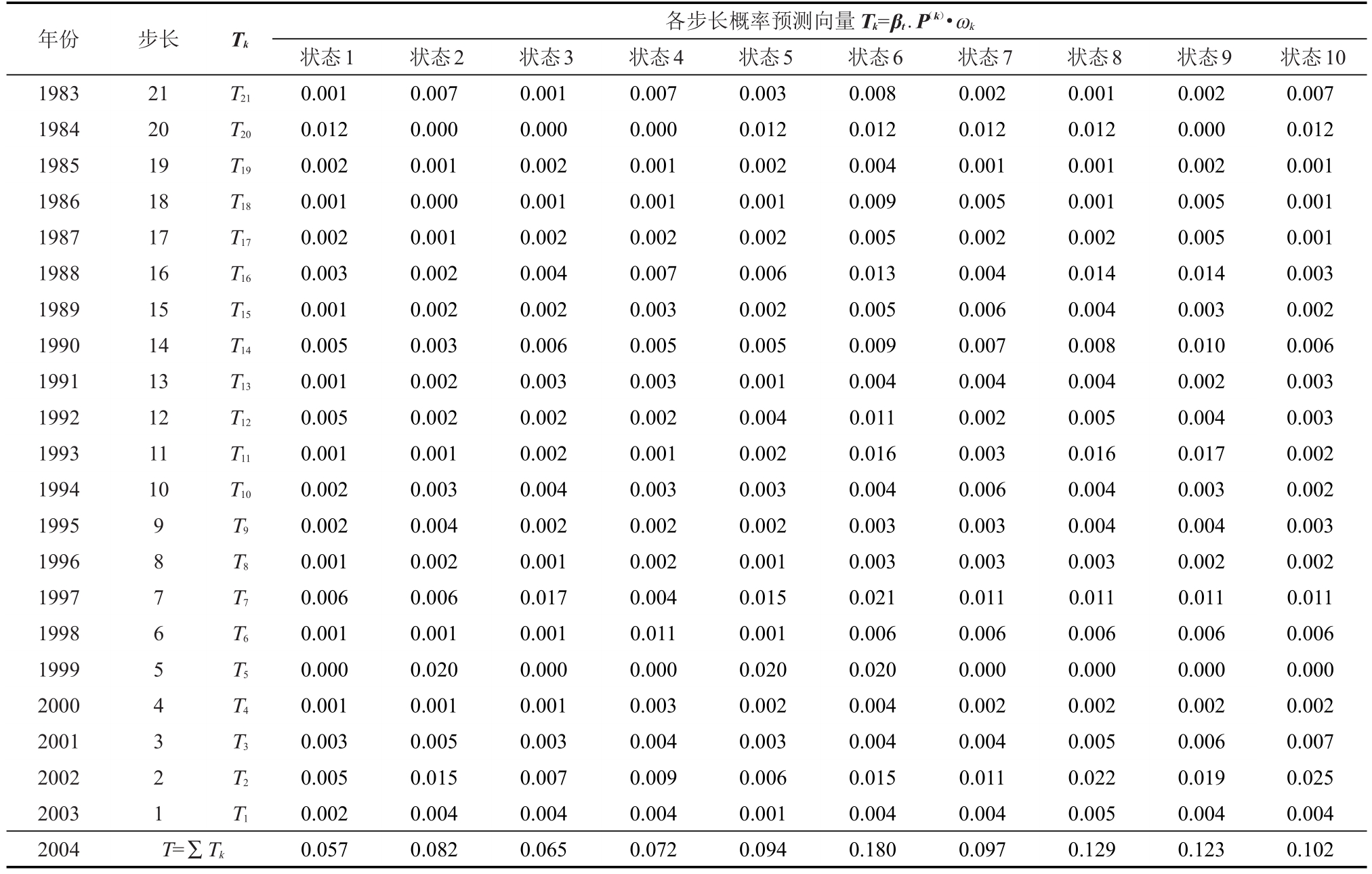
由表6可知,概率向量T中各元素的最大值为0.180,对应的状态为6,即该模型预测2004年的降水状态为6,由表1可知,承德市2004年的降水状态正是6,预测正确。
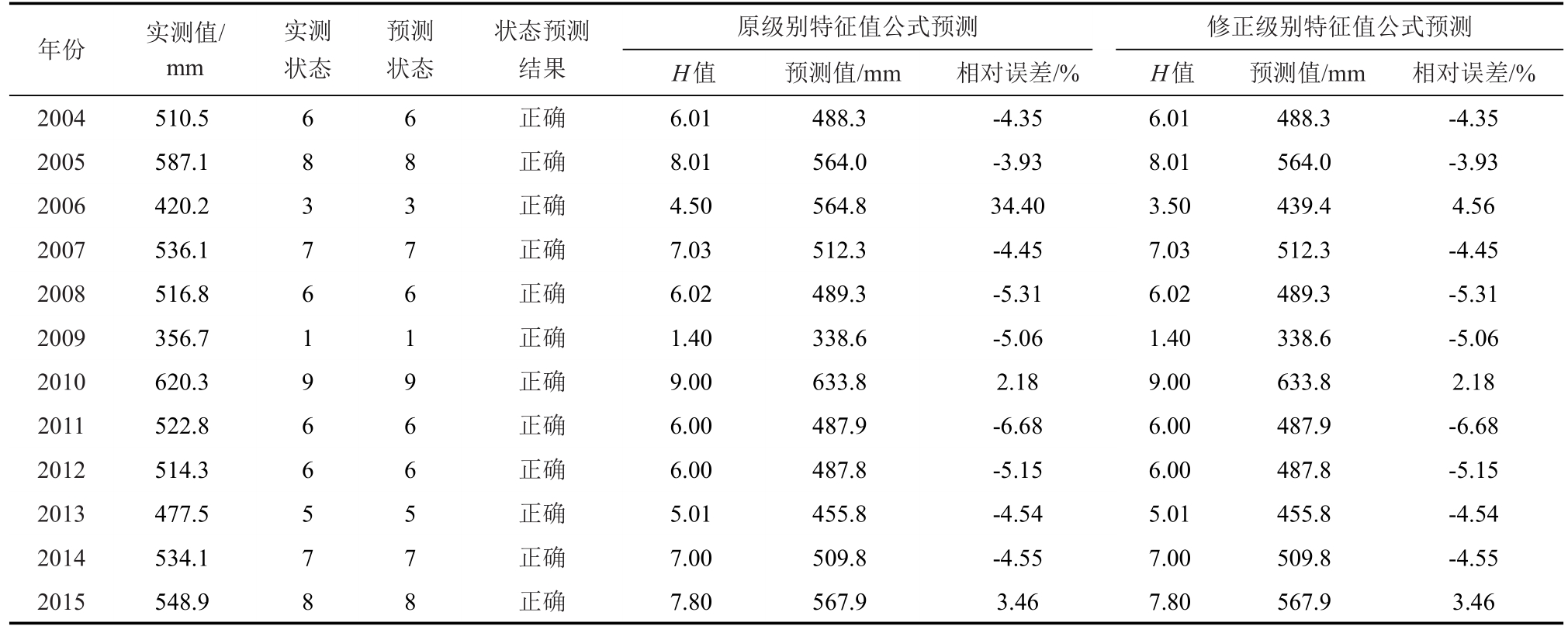
6)重复上述步骤逐年预测2005—2015年的降水状态,结果见表7。
表7 承德市2004—2015年降水预测结果
1)由加权马氏链得到的状态预测值i和级别特征值H之间并无关联,因此,常会出现H和i差值较大的情况,笔者在计算中发现当|H-i|<1时,预测精度普遍在可接受范围之内,而当|H-i|>1时预测精度随差值增大而显著降低,以H-i>1的情况为例简要分析。
因H-i>1,那么有H=i+0.5+a,其中a>0.5,根据式(9),此时的具体预测值为:
由式(14)最右端可知:预测值为二部分的和,由于Ui是真实值所在区间的上限,其值必大于等于真实值,所以第二项完全是误差增量,a越大(即H与i的差值越大),i越小,误差越大;同理可分析H-i<1的情况。鉴于此,尝试给出修正公式:

2)一般地,令级别特征值公式中的最大作用系数η=2或η=4,这种做法并不严谨。由级别特征值的计算公式知:随η增大,H值收敛于最大概率所对应的状态值i,因为待预测值为多个,有的是从大于i的方向收敛到i,有的是从小于i的方向收敛到i,所以,随η增大,因收敛方向不一各预测值的相对误差也在一定范围内变大或减小。由此可知,可能存在一些η使得所有预测值的相对误差都在可接受范围之内,基于此,本文经试算发现,其他参数固定,η=19时全局结果相对最佳。由此,分别用原公式和本文提出的修正公式预测承德市2004—2015年的降水量,结果见表7。
对表7分析可知,1)2004—2015年共计12 a的状态预测,结果全部与实际一致,表明该模型精度很高。
2)预测结果中既有相当于平水年状态的5、6,还包括了相当于偏丰、偏枯的状态3、8,尤其是包括了最小状态1和趋近极大值的状态9,可见涵盖范围广泛。而且状态1是实测序列中出现频次最低的,只有4次,状态10是出现频次最大的,达到10次,但预测结果中却出现了状态1,而没有出现状态10,这充分说明该模型预测的高精度是源于其合理的内在机制,与实测序列中状态出现的频次无显著关联。
3)2005年的降水状态为8,2006年就突降到3,2007年又突增为7,连续2次较大幅度的波动,尤其是2008年状态为6,2009年突然变为最小值1,2010年又陡然跨越8个状态变为9,跨度很大且连续突变,充分展示了年降水序列波动性大的特征,即使在这种情况下,该模型还是给出了正确的结果,说明基于模糊聚类的权马氏链适于波动性数据的预测。
4)由于2006年的H-i=4.5-3=1.5>1,因此该年预测值的相对误差达到了34.40%,属于预测错误。应用本文提出的修正后的级别特征值公式进行预测,结果如表7所示。由表7可知,所有预测值的相对误差全在7%以内,其中,低于5%的有8个,占总预测个数的67%。新公式对2006年降水预测的修正效果极为显著,使相对误差由34.40%降为4.56%。初步表明该修正公式精度良好。
5)综合以上分析知:本文所建模型合理可行,精度良好,可用于承德市年降水的预测。
应用所建模型,维持聚类数、聚类中心、模糊指数等参数固定不变,将每个预测的状态及数值加入原序列,计算预测值的隶属度,依此逐年预测了承德市2016—2020年的降水状态,并应用修正后的级别特征值公式计算具体降水量,结果见表8。
表8 承德市2016—2020年降水预测结果

由表8可知,据预测,2019年的降水量最少,但与承德市过去1951—2015年的平均降水量530.4 mm相比,差值不算很大,而且其降水状态为6,因此,2019年不会有显著的干旱影响;2016、2020年降水量与多年平均降水量基本持平;2017、2018年连续2 a降水状态为9,降水量都在600 mm以上,明显大于多年平均降水量,承德市应做好防洪防涝准备。
1)设定阈值对降水序列进行绝对划分是值得商榷的,尤其是阈值附近的降水量,其状态属性带有一定的模糊性,因此文章应用改进的FCM算法结合Xie-Beni有效性指标对年降水序列进行模糊聚类,在此基础上建立了权马氏链模型,将之应用于承德市2004—2015年降水状态预测,结果表明12个预测值全部与实际一致,模型效果非常理想。这初步表明,基于改进FCM算法的权马氏链适于进行年降水状态的预测且具有很好的预测精度。
2)在马氏链预测结果的基础上直接应用原级别特征值公式不甚合理,文章对此进行了简明分析并给出了修正公式。为便于比较,用原公式和修正公式分别预测了承德市2004—2015年的降水量,结果显示修正公式具有更高的精度,这说明在状态预测的基础上结合本文给出的修正公式进行具体值的预测是合理可行的。
3)应用文中所建模型和修正后的级别特征值公式预测了承德市2016—2020年的降水状态和降水量,结果表明,承德市降水相对偏丰,无太大波动,不会出现极丰极枯的情况,值得注意的是2017、2018年连续2 a降水状态为9,应提前做好防洪防涝准备。
4)当数据序列不能严格满足马氏性时,可采用加权的方法来修正,但加权马氏链步长的选择却一直无据可依,也只能通过试算确定,这不但增加了计算量,而且试算的结果也很难具有普适性,因此,如何在理论上确定步长是个值得关注和探讨的问题。
参考文献:
[1]温海彬.马尔可夫链预测模型及一些应用[D].南京:南京邮电大学,2012:7-31.
[2]黄华,蔡仁,穆振侠,等.基于模糊集修正加权马尔可夫模型在新疆降水预测中的应用[J].新疆农业科学,2015,52(10):1 891-1 898.
[3]张永库,尹灵雪,孙劲光.基于改进的遗传算法的模糊聚类算法[J].智能系统学报,2015(4):627-635.
[4]何嘉婧,王晋东,于智勇.基于模糊C-均值的改进人工蜂群聚类算法[J].计算机应用研究,2016,33(5):1342-1345.
[5]李中,苑津莎.不同相似度测量方式的模糊C均值聚类分析[J].计算机工程与应用,2011,47(18):17-18.
[6]廖力,周雪芹,邹强,等.基于模糊聚类迭代模型的洪灾评估标准计算方法[J].长江科学院院报,2015,32(2):34-38.
[7]熊拥军,刘卫国,欧鹏杰.模糊C-均值聚类算法的优化[J].计算机工程与应用,2015,51(11):124-128.
[8]郭新辰,郗仙田,樊秀玲,等.基于半监督的模糊C-均值聚类算法[J].吉林大学学报(理学版),2015,53(4):705-709.
[9]张慧哲,王坚.基于初始聚类中心选取的改进FCM聚类算法[J].计算机科学,2009,36(6):206-209.
[10]唐明会,杨燕.模糊聚类有效性的研究进展[J].计算机工程与科学,2009,31(9):122-124.
[11]朴尚哲,超木日力格,于剑.模糊C均值算法的聚类有效性评价[J].模式识别与人工智能,2015,28(5):452-461.
[12]鲍正益.模糊聚类算法及其有效性研究[D].厦门:厦门大学,2006:13-30.
[13]张宇献,刘通,董晓,等.基于改进划分系数的模糊聚类有效性函数[J].沈阳工业大学学报,2014,36(4):431-435.
[14]丁裕国,刘吉峰,王冀.气象水文应用马尔科夫链统计模拟[M].北京:气象出版社,2015.
[15]孙才志,林学钰.降水预测的模糊权马尔可夫模型及应用[J].系统工程学报,2003,18(4):294-299.
[16]王涛,钱会,李培月.加权马尔可夫链在银川地区降雨量预测中的应用[J].南水北调与水利科技,2010,8(1):78-81.
[17]宋新山,严登华,王宇晖,等.基于Markov模型分析黄淮海中东部地区540年来的旱涝演变特征[J].水利学报,2013(12):1 425-1 432.
Predicting Annual Precipitation Using the Weighted Markov Chain Solved by the Improved FCM Algorithm
MIAO Zhengwei1,XU Ligang2
(1.Department of Hydraulic Engineering,Hebei University of Water Resources and Electric Engineering,Cangzhou 061001,China;2.The Scientific Research Institute of the Water Conservancy of Ningxia,Yinchuan 750021,China)
Abstract:We predicted the annual precipitation from 1951 to 2015 in Chengde using the improved FCM algorithm.The precipitation series was firstly classified using the fuzzy clustering,from which 10 cluster centers and their associated membership matrix were obtained.The weighted Markov chain model was established based on the maximum membership principle and the calculated annual precipitation series,by using the standardized autocorrelation coefficients as the weights.We used the membership vector as the initial state vector and predicted the annual precipitation from 2004 to 2015 in Chengde;the calculated results agree well with the measurements.We introduced and modified the level characteristic value formula of the fuzzy set.Based on the predicted results from the Markov chain model,we predicted the annual precipitation from 2004 to 2015 using the modified level characteristics value formula.The relative error was less than 7%.The preliminary results show that the proposed model is reliable for predicting annual precipitation.
Key words:prediction;annualprecipitation;fuzzy clustering;FCM algorithm;weighted Markov chain;Chengde
中图分类号:P333
文献标志码:A
doi:10.13522/j.cnki.ggps.2017.10.020
苗正伟,徐利岗.基于改进FCM算法的加权马尔可夫链的年降水预测[J].灌溉排水学报,2017,36(10):114-121.
文章编号:1672-3317(2017)10-0114-08
收稿日期:2017-02-06
基金项目:河北省教育厅青年基金项目(QN2017096)
作者简介:苗正伟(1981-),男。讲师,硕士,主要从事水文水资源方面的研究。E-mail:newstart2017@sina.com
责任编辑:赵宇龙