图1 导叶相对位置示意图
吴晨晖，汤方平，石丽建，谢传流，张文鹏
（扬州大学水利与能源动力工程学院，江苏 扬州225100）
摘 要：为了研究不同导叶位置对S型轴伸式贯流泵装置水力性能的影响，设计了4种不同导叶相对位置的方案，并分别针对小流量(Q=0.8Q0)、设计流量(Q=1.0Q0)、大流量(Q=1.2Q0)3种工况下的S型轴伸贯流泵装置进行了数值模拟计算。对比数值模拟结果与试验结果，并分析计算结果的外特性与内特性，通过模型试验验证了数值模拟计算结果的准确性。结果表明，泵装置效率和扬程随导叶相对位置逐渐增大呈现先上升后下降的趋势，导叶与叶轮之间的相对距离存在最优值A=10 mm，在此位置时，泵装置效率和扬程相对最高，导叶体水力损失与出水流道水力损失相对最小，导叶体对于动能的回收能力强。小流量与设计流量工况下，出水流道进口平均涡角的大小随导叶相对位置先减小后增加，对应出水流道水力损失先下降后上升的趋势。大流量工况下，平均涡角不随导叶相对位置变化而变化。
关 键 词：S型轴伸泵；导叶位置；数值模拟；水力性能
S型轴伸贯流泵装置出水流道结构简单，水力损失较低，因而广泛应用于大型低扬程泵站[1]，如广西斗门西安泵站以及江苏扬州黄金坝泵站。随着数值模拟技术的发展，国内外的研究人员广泛采用数值模拟与模型试验相结合的方法研究S型轴伸贯流泵装置的水力性能[2-5]。国内一些学者针对导叶回收环量能力进行了研究，提出了泵装置导叶出口环量的分布及定量表示方法[6-9]。另一些学者探讨了不同导叶位置对泵装置水力性能的影响，得出了导叶相对叶轮位置的变化会对泵装置水力性能产生较大影响的结论[10-13]。由此可见，导叶作为泵装置中的次重要部件，具有很高的研究价值。
目前针对导叶位置对泵装置性能影响的研究较多，但是对于S型轴伸贯流泵装置研究较少，S型轴伸贯流泵装置出水流道由于有S型弯折段，与竖井式及灯泡式出水流道不同。因此，不同导叶相对位置对S型轴伸贯流泵装置水力性能的影响值得研究。在前人研究基础上，采用基于CFD数值模拟的手段，重点分析不同导叶位置方案下泵装置中导叶体及出水流道的水力特性，以期为S型轴伸贯流泵装置的优化设计提供一定理论基础。
计算模型中叶轮叶片数为3片，叶轮室直径300 mm，叶顶间隙取0.2 mm，叶片角度取0°。模型泵装置设计流量取225 L/s，叶轮转速为1 022 r/min；导叶片数为5。计算模型为整个泵装置，包括叶轮室、导叶室、进出水流道及其延长段，进出水流道各延长2.4 m。设计4种导叶相对位置，以叶轮与导叶叶片之间相距2 mm时为基准方案A=0 mm，每种方案导叶相对位置间隔10 mm，图1为叶轮与导叶间距A示意图。采用Turbo grid软件建立叶轮以及导叶的模型并进行网格划分，经检验，叶轮和导叶体在Turbo grid中画出的网格质量较好，且满足正交性要求。进出水流道及延长段在UG软件中建立，控制参数主要为收缩断面圆角与外部型线，通过调整各断面尺寸使各断面之间过度平顺，将模型导入ICEM中完成结构化网格划分。在满足网格无关性要求时，出水流道及其延长段网格数为478 898，进水流道及其延长段网格数为191 089，叶轮网格数为440 622，由于导叶位置不同，导叶网格也不完全相同，保持在530 000左右，装置总网格数保持在1 640 000左右，网格质量均大于0.35，网格角度介于24°～155°之间。计算模型及计算网格如图2所示。
图1 导叶相对位置示意图
图2 计算模型与模型网格
基于N-S方程，采用标准k-ε紊流模型来求解计算模型[14]。出口采用质量流量，设计流量Q为225 L/s，进口采用固定总压，总压设定为1个标准大气压。所有壁面为光滑壁面，采用无滑移边界条件，进出水流道延伸段表面设置为自由水面，自由水面对速度和湍动能均采用对称平面处理。计算采用Stage交界面处理叶轮与进水流道、导叶体之间动静耦合流动的参数传递，收敛精度设置为1.0×10-5。
1）导叶体水力损失∆h计算式为：
式中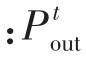
为导叶体出口断面总压（Pa）；
为导叶体进口断面总压（Pa）；ρ为水密度（kg/m3）；g为重力加速度（m/s2）。
2）压能恢复系数ξ计算式为：
式中：
为导叶体出口断面静压（Pa）；
为导叶体进口断面静压（Pa）。
3）平均涡角
计算式为：
式中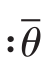
为平均涡角（rad）
为导叶出口断面平均切向流速（m/s）
为平均轴向流速（m/s）。
以设计流量工况为例进行分析，将设计流量下各方案下导叶的压力分布取出，如图3所示。
图3 导叶压力分布对比
由图3可知，高压区主要分布在导叶叶片压力面前缘，低压区分布在导叶叶片吸力面。随着导叶逐渐远离叶轮室，导叶叶片压力面前缘的高压区面积逐渐变少，导叶叶片吸力面与压力面后缘的低压区面积逐渐增大。对比方案A=0 mm与方案A=10 mm，2种方案导叶叶片吸力面低压区分布基本相同，方案A=10 mm的导叶叶片压力面高压区面积大小比前者小，压力梯度较小。对比方案A=10 mm、方案A=20 mm与方案A=30 mm，3种方案的导叶压力面高压区分布基本相同，方案A=10 mm导叶吸力面较高压力区的面积与相对较低压力区的面积比其余2种方案小。综合来看，当导叶相对位置为A=10 mm时，导叶体压力整体分布最好。
导叶设计应考虑能最大程度的回收叶轮出口的速度环量并尽可能减少导叶体本身的水力损失。由于叶轮旋转的影响，在经过导叶整流后，仍然有一部分剩余环量，造成出水流道内流态紊乱。将不同导叶位置下导叶出口的设计工况下的速度云图取出，如图4所示。
图4 导叶出口速度分布对比
由图4可以看出，出水流道进口速度分布因5片导叶的影响分成5块相似的区域，由于轴伸式出水流道在拐角处对水流的挤压作用，使得导叶出口速度偏向一边。导叶叶片根部由于切向速度的影响出现脱流，导叶根部的低速区面积随着导叶相对位置越来越远离叶轮呈现先减小后增加的趋势，低速区面积在导叶位置A=10 mm时最小。在设计流量下，导叶尾部的高速区域随着导叶相对位置的增加逐渐向逆时针方向扩散并且在导叶位置A=10 mm时扩散程度最小。由此可见，虽然在A=10 mm时依然存在局部低速区和局部高速区，但速度分布的均匀度总体优于其他导叶位置。
计算不同导叶相对位置的从导叶进口到出口区域的导叶水力损失如图5所示。由图5可知，在小流量工况以及设计流量工况下，随着导叶逐渐远离叶轮，导叶体水力损失呈先减小后上升的趋势。在大流量工况下，导叶体水力损失呈现微弱的波动。在3种工况下，当导叶相对位置为A=10 mm时，导叶体水力损失最小。由此可以得出，随着流量逐渐上升，导叶相对位置对导叶体水力损失的影响越来越小。
图5 导叶体水力损失对比
图6 压能恢复系数对比
设置导叶的其中一个目的是为了回收动能转化为压能，采用静压回收系数ξ反映不同导叶位置在相同流量下对压能的回收程度，将各流量工况下不同方案泵装置导叶体的压能恢复系数取出，如图6所示。在小流量和设计流量工况下，压能恢复系数随着导叶相对位置的增加先增加后减少。在大流量工况下，导叶相对位置的变化对压能恢复系数影响不明显。流量的大小与其对导叶回收能量能力影响的程度成反比关系。在3种工况下，导叶相对位置A=10 mm时导叶体回收动能的能力最强。
为进一步分析不同导叶位置对S型轴伸泵出水流道水力性能的影响，将计算模型中出水流道单独取出，计算由出水流道进口到出口的水力损失，结果如图7所示。
由图7可以看出，出水流道内部的水力损失并不是与流量呈现递增的关系，而是存在最小值。在3种工况下，出水流道水力损失随着导叶相对位置变大呈现先减小后增加的趋势。导叶相对位置上升到A=20 mm之后，水力损失逐渐趋于平滑。出水流道水力损失存在最小值，位于设计流量下导叶相对位置A=10 mm处。
图7 出水流道水力损失对比
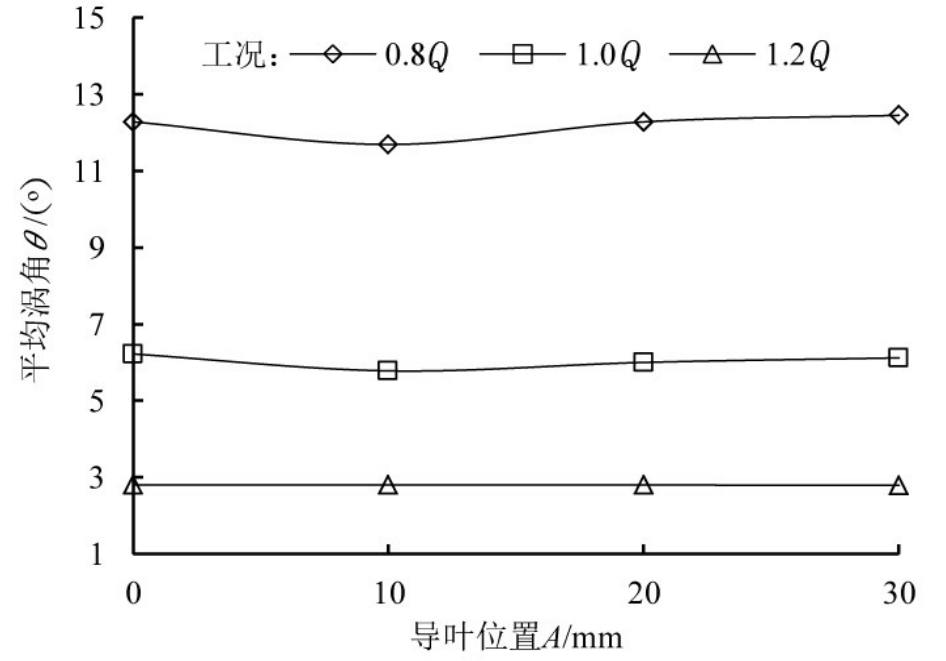
图8 平均涡角对比
导叶出口的剩余环量是对出水流道水力损失产生影响的一个重要因素。为进一步分析不同导叶位置对于出水流道水力损失的影响，应用文献[15]中关于平均涡角的概念（平均涡角可以反映导叶出口的剩余环量分布），将计算得出的不同流量下出水流道进口平均涡角数据整理成图，如图8所示。
由图8可知，在导叶位置一定的情况下，平均涡角的大小随着流量上升逐渐减小，这是由于小流量时，过水断面面积一定，水流轴向速度较小，绝对速度切向分量相对较大，叶轮出口环量较大，从而导致从导叶中流出的剩余环量较大，出水流道进口平均涡角较大；在大流量时，水流轴向速度较大，绝对速度的切向分量相对较小，导叶出口剩余环量较小，因此，出水流道进口平均涡角较小。在小流量工况与设计流量工况下，导叶出口平均涡角呈现出当导叶相对位置逐渐增加先减小后增加的趋势，对应图7中出水流道水力损失先下降后上升的趋势，在导叶相对位置增加到A=20 mm之后，涡角没有发生明显变化，当导叶相对位置A=10 mm时平均涡角最小，对应出水流道的水力损失最小。在大流量工况下，平均涡角的大小基本不受导叶相对位置的影响，不同导叶相对位置下的平均涡角的大小基本保持不变。
如图9所示，在小流量工况以及设计流量工况下，随着导叶相对位置逐渐远离叶轮，扬程呈现先上升后下降的趋势。在小流量工况下，扬程变化趋势比设计流量工况下2种工况变化更明显，在大流量工况下，导叶相对位置对装置扬程影响不明显。在3种工况下，当导叶相对位置为A=10 mm时，装置扬程最高，在导叶相对位置由A=20 mm增加到A=30 mm的过程中，扬程没有明显变化。由此可得出，随流量上升，导叶相对位置对装置的扬程影响越来越小，导叶与叶轮之间的距离存在最优值。
图9 扬程对比曲线
图10 效率对比曲线
如图10所示，在小流量工况、设计流量以及大流量工况下，随着导叶相对位置由A=0 mm增加到A=20 mm的过程中，S型轴伸贯流泵装置效率先上升后下降,并且在导叶相对位置上升至A=20 mm之后，装置效率基本不随导叶相对位置变化而变化。
在小流量、设计流量以及大流量工况下，导叶相对位置A=10 mm时，泵装置外特性以及内特性都保持较好水平，因此选择导叶相对位置A=10 mm为最佳方案。
对最佳方案导叶相对位置A=10 mm的S型轴伸贯流泵装置进行模型试验。模型试验在扬州大学高精度水力机械试验台上进行。实验台水力封闭循环系统的总长度为60 m，管道直径为0.5 m，仅在安装电磁流量计的前后10倍直管段为直径0.4 m管道，整个系统水体积为50 m3试验台鉴定，效率测试系统综合不确定度为±0.39%，满足国家GB/T18149—2000和中华人民共和国水利部行业标准SL140—2006精度要求，通过国家计量认证。图11为模型现场测试段照片，叶轮、叶轮室与导叶体均为数控加工成型，进出水流道及其延长段则是由不锈钢材料制作完成。
由图12可以看出，在设计流量和大流量工况下，数值模拟流量-扬程曲线与模型试验流量-扬程曲线吻合度较高。在小流量工况下，数值模拟扬程曲线略低于模型试验扬程曲线。数值模拟流量-效率曲线在大流量工况下略高于试验效率曲线而在小流量工况下略低于试验曲线。总体而言，数值模拟数据与模型试验吻合度较高，整体趋势保持一致，各点误差都在±3%以内。试验结果与数值模拟得到相互验证，数值模拟计算结果可信。
图11 模型试验泵装置
图12 叶片角度为0°时泵装置试验与数值模拟外特性曲线对比
1）在当导叶位置为A=10 mm时，导叶体水力损失最小，导叶体对动压的回收能力最好，出水流道进口平均涡角最小，出水流道水力损失最小，因此,泵装置在3种工况下扬程效率均最高。
2）对于S型轴伸贯流泵装置来言，叶轮与导叶之间相对位置的变化会对泵装置的扬程效率产生影响，导叶相对叶轮距离存在最优值使得S型轴伸贯流泵装置性能最优。而当叶轮导叶之间距离增加到一定值后，泵装置性能不再受到导叶相对位置的变化而产生明显的影响。
针对S型轴伸贯流泵装置的能量性能，研究得出导叶与叶轮之间的距离存在最优值的结论。该研究结论与杨从新等[16]关于立式泵装置的研究结果一致，主要原因是对于某一特定导叶，导叶形状已固定，导叶进口角已确定，无论导叶是靠近或远离叶轮，水流在进入导叶时都会造成较大的进口冲击损失，使得导叶相对叶轮的位置存在一个最优值，该最佳位置使得叶轮出口的水流能够更为平顺,以尽可能小的冲角进入导叶。兹主要针对泵装置能量性能进行研究，除此之外，叶轮属于动叶，导叶属于静叶，动静干涉作用是旋转机械领域另一研究热点。因此，导叶与叶轮之间距离的变化可能会对导叶进口压力脉动产生影响，可以在压力脉动方面做进一步研究。
参考文献：
[1]刘超.轴流泵系统技术创新与发展分析[J].农业机械学报,2015,46(6):49-59.
[2]WANG Zhengwei,PENG Guangjie,ZHOU Lingjiu,et al.Hydraulic performance of a large slanted axial-flow pump[J].Engineering Compulations,2010,27(2):243-256.
[3]ZHANG Desheng,SHI Weidong,CHEN B,et al.Unsteady flow analysis and experimental investigation of axial-flow pump[J].Journal of Hydrodynamics,2010,22(1):35-43.
[4]杨帆,刘超,孙丹丹,等.轴流泵装置虹吸式出水流道内流机理数值分析[J].农业机械学报,2015,46(6):60-65.
[5]徐磊,刘超,王芃也,等.平面S型轴伸泵装置变转速水力特性[J].灌溉排水学报,2016,35(11):30-34.
[6]汤方平,周济人,鄢碧朋.轴流泵后导叶回收能量分析[J].水泵技术,1995(3):19-22.
[7]成立,刘超,周济人,等.低扬程灌排泵装置进出水流道研究进展及展望[J].灌溉排水学报,2008,27(1):112-114.
[8]梁金栋,陆林广,徐磊,等.轴流泵装置导叶出口速度环量对出水流道水力损失的影响[J].农业工程学报,2012,28(1):55-60.
[9]谢荣盛,汤方平,刘超.轴伸式出水流道内流场数值模拟分析[J].农业机械学报,2016,47(8):40-51.
[10]王文杰,袁寿其,裴吉.导叶安装位置对余热排出泵内流特性的影响[J].排灌机械工程学报,2014,32(9):61-67.
[11]周岭,杨阳,施卫东,等.导叶出口边位置对深井离心泵性能的影响[J].排灌机械工程学报,2016,34(12):24-33.
[12]孟凡,裴吉,李彦军,等.导叶位置对双向竖井贯流泵装置水力性能的影响[J].农业机械学报,2017,48(2):52-57.
[13]戴景,戴启璠,王宏图.扩散导叶叶片位置对灯泡贯流泵装置水力性能的影响[J].水电能源科学,2017,35(1):7-11.
[14]许洪元,吴玉林,高志强.稀相固粒在离心泵轮中的运动实验研究和数值分析[J].水利学报,1997(9):12-16.
[15]FINNIE I.Erosion of surfaces by solid particles[J].Wear,1960,3(2):87-103.
[16]杨从新,杜嫒英，黎义斌.叶轮与导叶体之间的距离对混流泵水阻系数及效率的影响[J].流体机械,2012,40(10):48-55.
Effect of the Position of Guide Vane on Hydraulic Performance of the S-shaped Extension Pumping System
WU Chenhui,TANG Fangping,SHI Lijian,XIE Chuanliu,ZHANG Wenpeng
(School of Hydraulic,Energy and Power Engineering,Yangzhou University,Yangzhou 225127,China)
Abstract:The influences of guide vane position on hydraulic performance of the S-shaped extension pumping system were studied in this paper numerically.We considered four positions and three flow conditions:designed flow(Q0),reduced flow(0.8Q0)and fast flow(1.2Q0).The results showed that with the relative position ofthe guide vane increasing,the efficiency and lifting height of the pump increased first before declining.The optimal relative distance between the guide vane and the impeller was 10 mm at which the energy loss in both the impeller body and the outlet passage was minimal,the pump efficiency and lift height peaked,and the guide vane was most effective in recovery of the kinetic energy.Under the reduced and designed flow rates,the average inlet vortex angle of the outlet passage and energy loss at the outlet passage decreased first before increasing.Under high flow rate,in contrast,the average vortex angle remained constant,independent of the relative position of the guide vane.
Key words:S-shaped extension pump;guide vane position;numerical;hydraulic performance
中图分类号：TH312
文献标志码：A
doi：10.13522/j.cnki.ggps.2017.11.012
吴晨晖，汤方平，石丽建，等.导叶位置对S型轴伸贯流泵装置水力性能的影响[J].灌溉排水学报，2017,36（11）：63-69.
文章编号：1672-3317（2017）11-0063-07
收稿日期：2017-05-20
基金项目：国家自然科学基金项目（51376155，51609210）；中国博士后科学基金项目（2016M591932）；江苏高校优势学科建设工程项目（PAPD）；江苏省科研创新计划项目（KYZZ16_0492）
作者简介：吴晨晖（1994-）,男,浙江湖州人。硕士研究生，主要从事泵装置理论研究。E-mail:1094617491@qq.com
通信作者：汤方平（1964-）,男，浙江武义人。教授，博士生导师，主要从事泵装置多学科优化设计研究。E-mail:tangfp@yzu.edu.cn
责任编辑：陆红飞