
石 喜1,孙 斌2,柴媛媛3,乔雅男1
(1.兰州交通大学土木工程学院,兰州730070;2.郑州大学水利与环境学院,郑州450001;3.甘肃省水土保持科学研究所,兰州730020)
摘 要:为了研究灌溉管网非恒定流计算机实现方法,基于非恒定流的基本原理及其特征线(MOC)解法,探讨了采用节支关联表和支节关联表建立管网结构信息,并对管网数据进行储存、计算和结果输出的方法,在计算过程中通过数组储存不同的节点类型及管网参数供计算机调用。通过实例对典型喷灌管网的非恒定流过程进行了计算并分析。结果表明,该方法储存管网结构信息简单方便,计算机能够快速识别节点类型并调用相应的边界条件子程序,本方法可用于复杂灌溉管网的非恒定流建模与分析。
关 键 词:灌溉管网;非恒定流;计算机方法
与传统渠道输配水方式相比,管网输水具有节水省工、提高土地利用率、易于实现自控等优势[1]。然而随着灌溉管网的发展,也引起了诸多问题,如管网压力分布不均匀、管网非恒定流现象等。其中非恒定流也称水锤或水击,是指当压力管道中的流体因某些原因产生流速的急剧变化而引起管道内流体压力沿管系迅速传播、急剧变化的现象[2]。产生流速变化的原因可能是阀门的突然关闭、水泵的突然停止或管道气体的存在等。在灌溉管网中,由于管道组成较多,任意一级管道出现问题都会对整个管网造成影响,轻则影响灌水质量,重则引起爆管事故造成管网瘫痪。
国内外学者对不同类型管网的非恒定流进行了研究[3-6],形成了比较成熟的理论基础,然而对于灌溉管网大多研究以恒定流为主,对于复杂的非恒定流过程尚难以准确描述[7]。在管网非恒定流计算时,需借助计算机完成不同时刻的迭代计算,因此如何快速表达管网的拓扑结构并转换成计算机信息输入是复杂管网非恒定流建模要解决的首要问题。曹慧哲等[8]对基于图论的环状管网慢变流模型进行了分析。彭继军等[9]研究了燃气管网水力计算图的计算机生成方法。李成乐等[10]探讨了燃气管网水力计算图节点计算机自动编号的方法。在管网非恒定流计算时,建立简单快速的管网结构表达方式及数据输入和计算方法仍需进行研究。为此,探讨采用节支关联表和支节关联表建立管网信息,并对管网信息数据进行储存、计算和结果输出的方法,通过实例进行分析,并对所建立的方法进行评价。
描述管网中任意管段非恒定流的控制方程为运动方程和连续性方程,即:

式中:V为流速(m/s);t为时间(s);x为沿管轴线的轴向坐标(m);g为重力加速度(m/s2);f为摩擦系数;D为管道直径(m);H为水头(m);α为管道倾角;a为水锤波速(m/s)。
式(1)和式(2)是一组双曲型偏微分方程组,在计算域内存在着2条特征线,沿着这2条特征线可将方程组转化为常微分方程,从而易于数值求解。特征线法首先设一未知因子λ,将式(1)、式(2)通过线性组合进行合并[11],即:
根据全微分法则,令:
则有:
将式(5)带入式(3)后,并略去V和α可得2组常微分方程式:
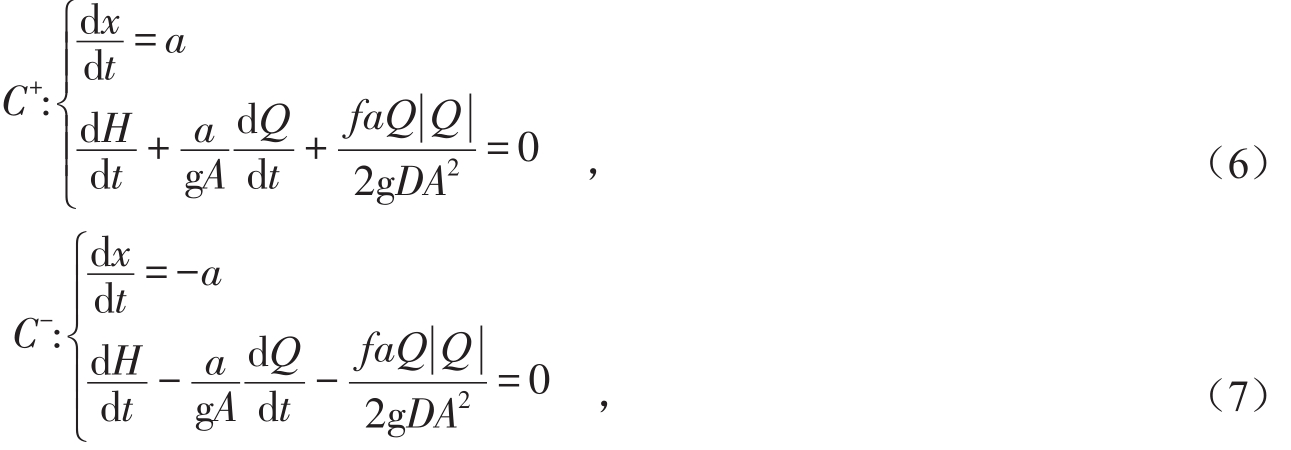
式中:A为任意管段的截面积(m2)。
将式(6)和式(7)表述的2组常微分方程式沿图1所示的x-t平面上的矩形网格进行有限差分,通过对摩阻项进行显示格式处理,并沿特征线C+和C-进行积分离散化后得到的相容性方程如下:
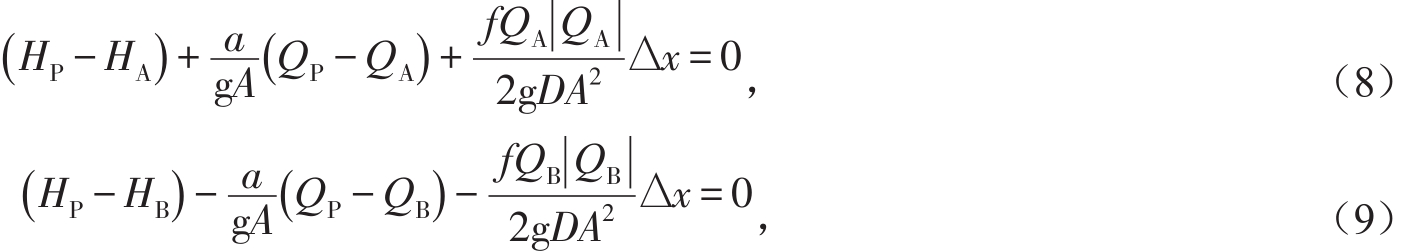
式中:HA、HB为图1中A、B点的水头(m);QA、QB为A、B点的流量(m3/s);HP为P点的水头(m);QP为P点的流量(m3/s);△x为A、B点之间的距离(m)。
为了便于计算,上述相容性方程进一步改写为:
式中:CP=HA+BQA-R|QA|QA;CM=HB-BQB+R|QB|QB;管道特征常数B=a/(gA);摩阻特性常数R=fΔx/(2gDA2)。
根据水泵的运行特性曲线,结合相容性方程可得运行水泵的边界条件。
式中:QP为流经水泵的流量(m3/s);HP为水泵中心压力(m);Hs为水泵关死点扬程(m);a1、a2为水泵特性常数。
由喷头水流的连续性方程和相应的相容性方程,可得到喷头边界条件,即:
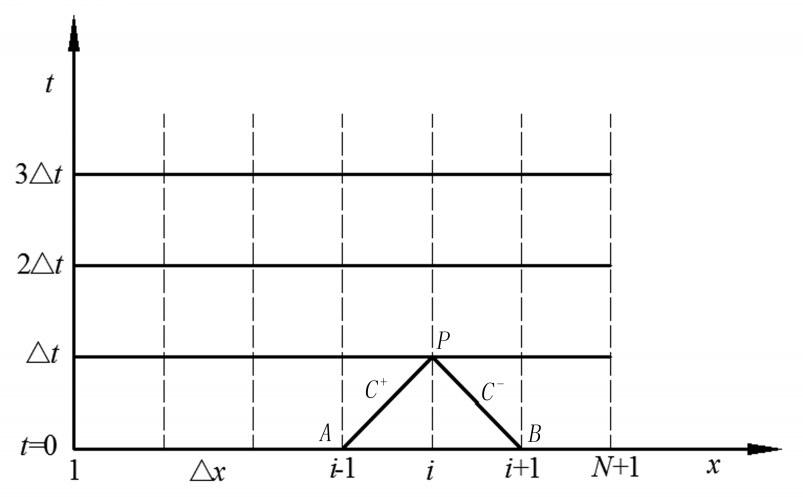
图1 特征线网格

式中:Cd为喷头流量系数;Aj为喷嘴过流面积(m2)。
根据三通管的连续性方程并忽略节点处的压力损失,结合相容性方程可得三通管的边界条件,即:

式中:QP1、QP2、QP3分别为三通管进口和2个出口断面的流量(m3/s);HP1、HP2、HP3分别为三通管进口和2个出口断面的压力(m)。
对于非恒定流动,阀门在启闭过程中,瞬时流动的压力降和流量关系按孔口出流公式表达,结合相容性方程可得到阀门在关闭过程中的边界条件方程。
式中:CV=(Q20τ2)/2H0;τ为无量纲阀门相对开度,τ=CDAG/(CDAG)0;H0为阀门全开定常状态时的水头(m);Q0为通过阀门的流量(m3/s);CD为阀门流量系数;AG为阀门过流面积(m2)。
在应用特征线法计算时,必须采用统一的时间步长△t,这对于复杂管网来说往往难以满足。为了保证统一的时间步长及整数分段数,一般要进行处理,否则要采用插值的特征线法。兹采用调整波速法[11]进行处理,其基本思路为:在管网中由于实际的水锤波速很难计算准确,因此可以适当调整波速,使计算分段数Nj为整数,从而满足特征线法时间步长的一致性。即令:
式中:ψj为波速修正系数,通常ψj<0.15;Nj为第j个管段的分段数;Lj为第j个管段的长度(m)。
特征线法的有限差分方程稳定收敛的必要条件是满足Courant-Lewy稳定条件,即差分方程问题的依赖区间必须包含相应微分方程问题的依赖区间:
在应用该特征线法计算时,通过调整波速法保证采用的时间步长△t是固定不变的,所以这样的差分计算格式也称为规定时间网格法,每个时间步长网格点上的未知量可直接求出,因此满足稳定性和收敛性。
由于管网系统结构形式复杂,水力组成元件较多,如果绘制每个元件的形状图则非常烦琐,从管网分析的角度而言也无必要。在非恒定流计算时一般只关心每个管段和相应管件在不同时刻的压力和流量,因此可将复杂管网进行简化处理。采用有向线性图来表示管网中管段与管件的连接关系,即用一条线段表示管段,称为支路;用小圆圈或小黑点表示水泵、阀门、交汇点等,称为节点;然后用箭头表示水流的方向。在管网线性图中,支路与节点的相互关系可分为3种:①支路的参考方向指向某一节点,称支路与节点正向关联;②支路的参考方向离开某一节点,称支路与节点负向关联;③支路与节点无任何关系,称无关联。图2为某枝状管网用有向线性图的表示形式,图2中1,2,3…表示管网节点编号;①,②,③…表示支路编号。
管网线性图的结构可用支节关联表来储存,即给出了每一条支路与其连接节点的对应关系。由于支路的方向是由进口节点指向出口节点,所以在已知支路进口节点和出口节点编号的情况下,可以画出有向线性图。对于如图2所示的管网,用支节关联表储存的方法如表1所示。
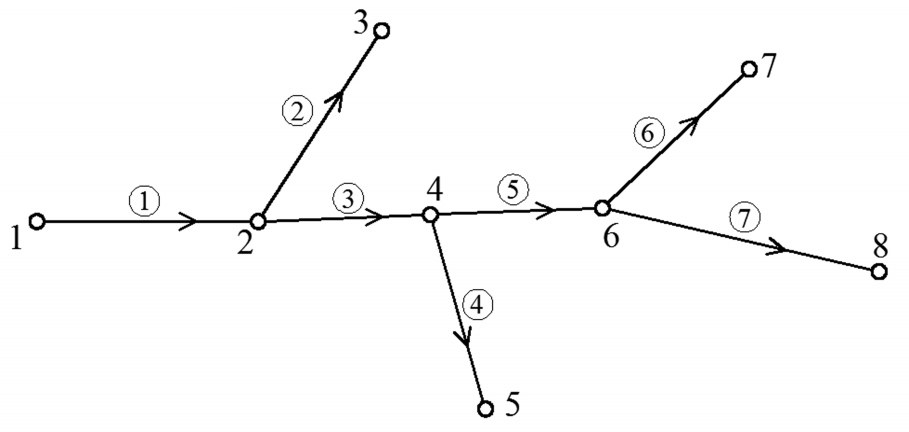
图2 管网有向线性图
表1 支节关联表

在管网非恒定流计算时,往往要调用不同边界条件的子过程,需要知道某一节点与其所有连接支路的关系,可用节支关联表来表示管网中每个节点与其关联支路的对应关系,在表示时定义流进该节点的管段号为正值,流出该节点的管段号为负值。对于如图2所示的管网,其节点与支路的关系用节支关联表储存的方法如表2所示。
表2 节支关联表

灌溉管网中常见的节点类型有以下几类:①压力随流量变化的节点,如运行中的水泵、阀门、喷头等;②压力不变的节点,如水塔、蓄水池等;③压力相等的普通节点,如三通、变径管、弯头等。利用计算机进行非恒定流计算时,需要调用不同的边界条件子程序,因此要识别不同的节点类型。可用一维数组LX(i)储存节点类型,如LX(1),LX(2),…,LX(N)分别表示节点1,2,…,N的类型代号。对于如图2所示的管网,若系统进口为水泵,出口为自由出流,用1、2、3分别代表水泵节点、分岔节点和自由出流节点,则节点类型表示为:LX(1,2,3,2,3,2,3,3)。
为了便于计算机计算分析,首先要输入储存管网信息、原始数据和其他初始数据(如初始时刻的压力和流量)。用二维数组Q(j,i)和H(j,i)分别表示管网中各支路计算断面在t时刻的流量和压力;用二维数组QP(j,i)和HP(j,i)分别表示计算断面在t+△t时刻的流量和压力。其余数据如管径d、管长l、水锤波速a、沿程阻力系数λ、局部阻力系数ζ等分别用不同的一维数组来储存,储存的数据可采用Excel表格输入,供程序调用。数据的输出也可采用Excel表格,只需输出所需管段和节点的计算结果即可。
管网非恒定流计算的主要步骤为:①读入管网基本数据,如支节关联表、节支关联表及其他数据表。②计算管道特性常数B、摩阻特性常数R及管网中各管段的水锤波速a,采用调整波速法确定统一的时间步长,并将各管段分段。③计算每个管段节点在初始t时刻的压力H和流量Q并储存。④增加时间步长△t,首先核对增加的t+△t时刻是否超过最大计算时间Tmax,如果超过则计算结束;如果未超过则进行t+△t时刻的参数计算,分别求出内节点和边界节点的压力HP和流量QP。⑤储存结果HP和QP,并将计算得到的HP和QP赋值给H和Q,作为下一个计算时刻的初值参数。⑥重复以上步骤④~步骤⑤,直到计算时刻T>Tmax结束。
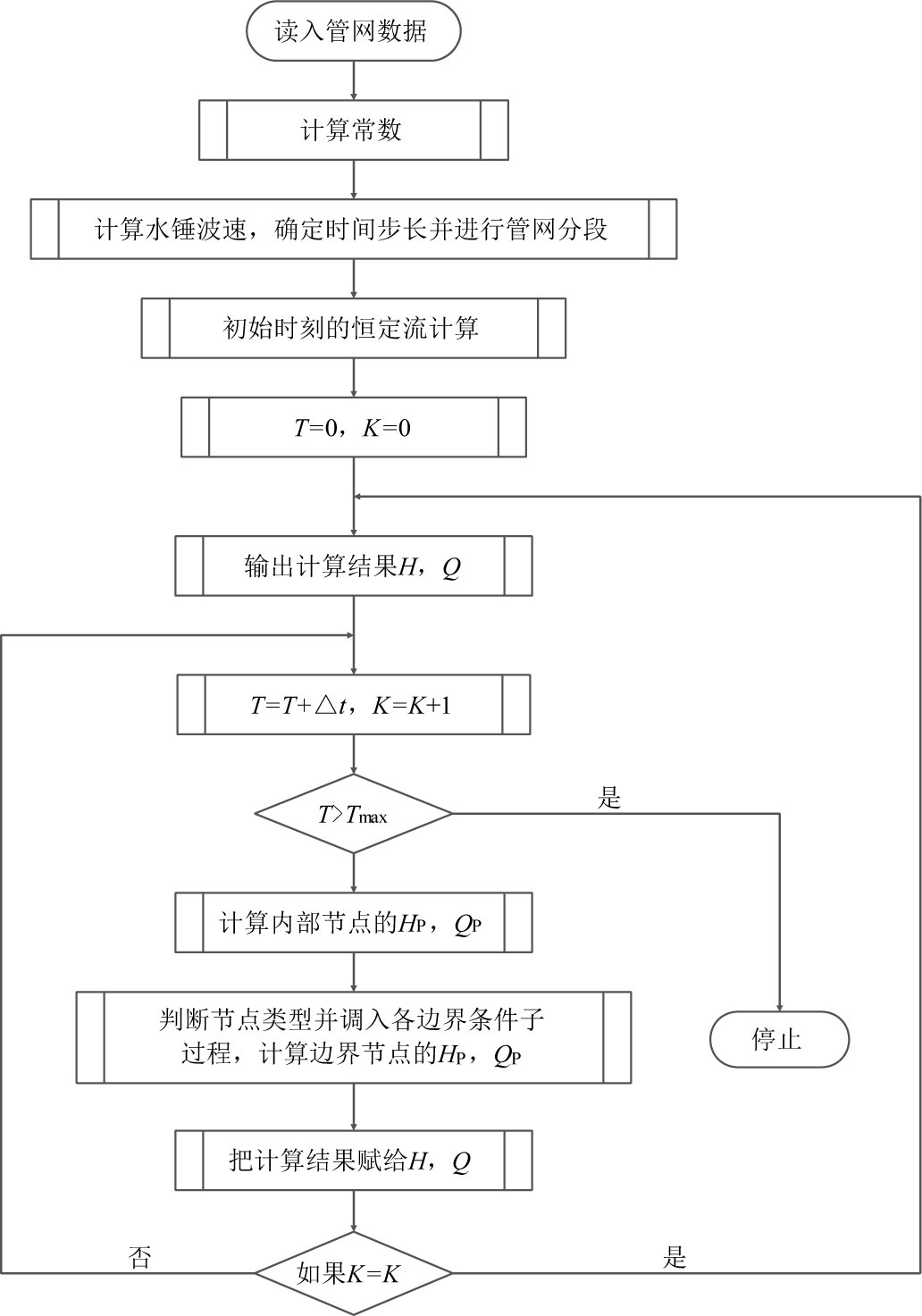
图3 管网非恒定流计算流程
某梳齿形喷灌管网布置如图4所示,管网由1条干管和6条支管组成,每条支管上有6个竖管喷头组合,在支管的进口安装阀门用来调节流量,管网的具体参量见表3。按上述原理通过编程进行非恒定流过程计算,分别建立描述管网结构信息的支节关联表和节支关联表并通过EXCEL进行数据输入和输出。计算时假设支管6上的阀门在0.3 s内突然关闭,阀门关闭规律按幂函数τ=(1-t/tc)1.5规律,分析管网中由于阀门突然关闭产生水锤压力传播过程。
图5为支管6上的阀门在0.3 s内突然关闭时管网监测点P1点的水锤压力波动曲线。由图5可知,阀门突然关闭时,水锤压力在0.89 s时达到最大值82.7 m,为恒定流时水头的2.58倍(恒定流水头为32.0 m)。图6为干管中监测点P1—P6的最大水锤压力,可见P1点的水锤压力最大,并沿干管入口不断减小,说明管网水锤压力的最大值产生在操作阀门处。
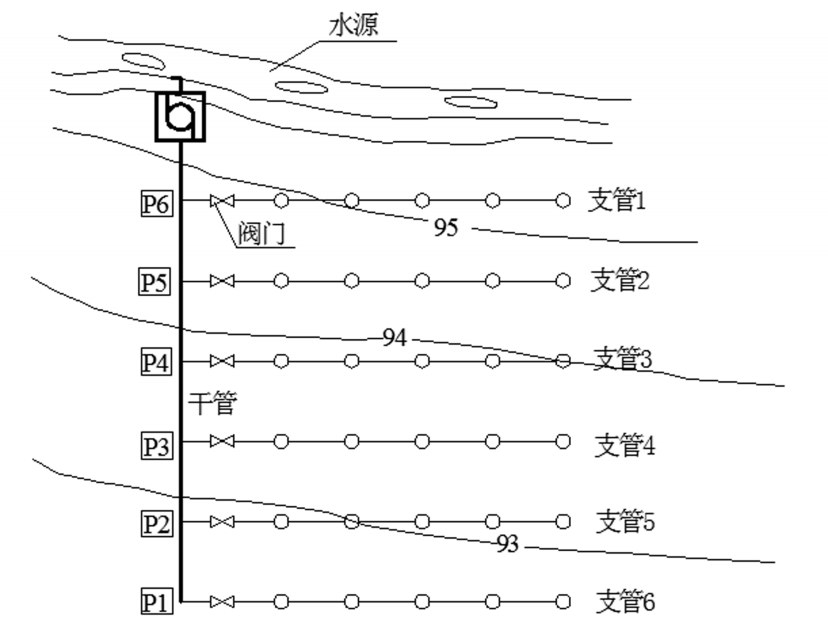
图4 典型喷灌管网布置图
注 P1—P6表示管网压力监测;“93”、“94”、“95”表示地形高程(m)
表3 喷灌管网非恒定流计算有关参量

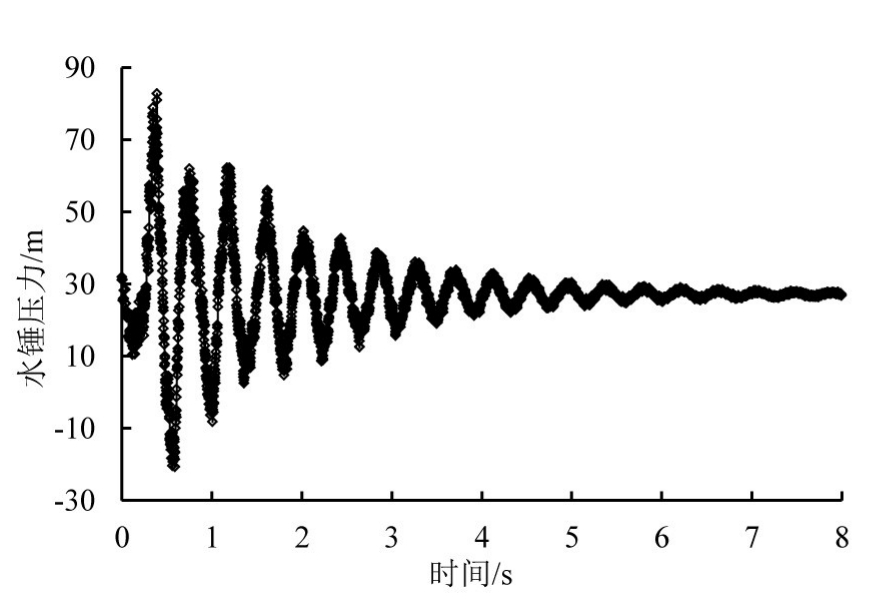
图5 管网监测点P1压力波动过程线
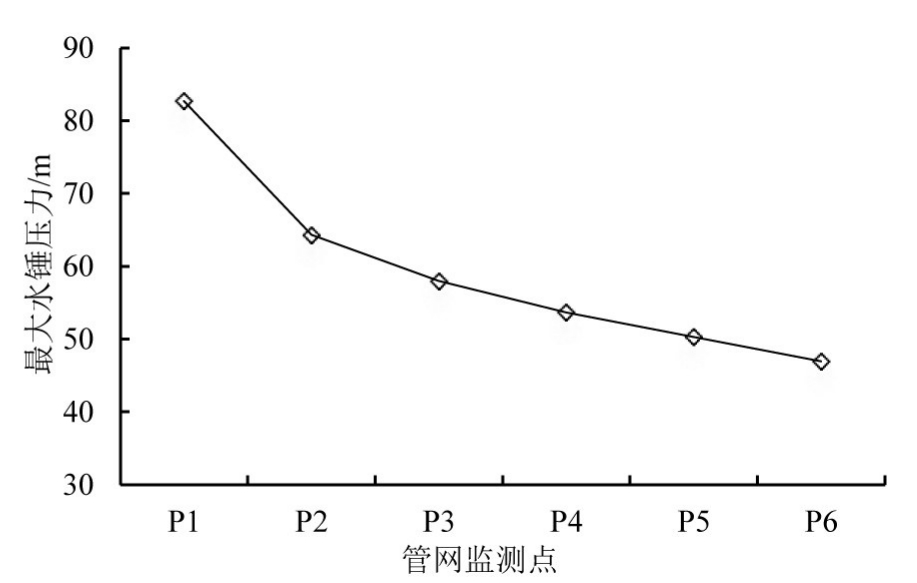
图6 管网监测点最大水锤压力
1)特征线法由于理论严密、计算精度高、编程方便等优点,在各类管道的非恒定流计算中得到广泛应用,尤其对于复杂管网,特征线法可以很好地处理各类边界问题。随着灌溉管网结构形式的不断规模化和复杂化,特征线法的应用将会越来越广泛。
2)基于特征线法的基本原理,在管网非恒定流计算时,通过支节关联表和节支关联表建立管网的拓扑结构信息,然后通过数据输入、程序调用管网信息完成管网的非恒定流计算过程。实例计算表明采用支节关联表和节支关联表储存管网结构信息简单方便、易输入,计算机能快速识别各类节点的类型及数据信息。
3)管网中阀门突然关闭时,管网产生很高的水锤压力并在管网中传播,最大水锤压力发生在操作阀门处,离阀门越远最大水锤压力越小,这与文献[12]的结果一致。
对于特别复杂的管网,由于支路和节点数量众多,数据输入时容易出错,导致计算结果不准。因此,在数据的输入方法上还需进一步优化,研究更加简洁、方便的数据输入方法。
参考文献:
[1]付玉娟,蔡焕杰.灌溉管网优化研究现状与展望[J].西北农林科技大学学报(自然科学版),2005,33(11):137-140.
[2]吕宏兴,裴国霞,杨玲霞.水力学[M].北京:中国农业出版社,2002.
[3]GARGOURI J,HADJ-TAIEB E,SCHMITT C,et al.Failure conditions analysis of looped network pipes due to water hammer phenomenon[J].Mecanique&Industries,2011,12(2):121-137.
[4]OUCHIHA Z,LORAUD J C,GHEZAL A,et al.An investigation of highly pressurized transient fluid flow in pipelines[J].International Journal of Pressure Vessels and Piping,2012,92:106-114.
[5]章少辉,刘群昌,白美健,等.规模化灌溉管网非恒定流模拟研究[J].灌溉排水学报,2014,33(4/5):325-30.
[6]李江云,汪慧,陈知超,等.给水管网拓扑结构对供水行为压力波动的影响[J].中国给水排水,2015,31(13):49-53.
[7]武阳,李益农,刘群昌.大规模灌溉管网的发展分析与研究[J].中国农村水利水电,2015(1):1-3.
[8]曹慧哲,贺志宏,何钟怡.基于图论的环状管网慢变流的计算研究[J].哈尔滨工业大学学报,2007,39(10):1 559-1 563.
[9]彭继军,田贯三,刘燕.燃气管网水力计算图的计算机生成[J].山东建筑工程学院学报,2003,18(1):58-62.
[10]李成乐,田贯三.燃气管网水力计算图节点计算机自动编号的方法[J].山东建筑工程学院学报,2005,20(4):51-54.
[11]王学芳,叶宏开,汤荣铭.工业管道中的水锤[M].北京:科学出版社,1995:58-77.
[12]郑大琼,赵晓利,张国斌,等.城镇供水管网瞬变流计算[J].中国给水排水,2006,22(6):42-45.
Simulating Unsteady Flow in Irrigation Pipe Network
SHI Xi1,SUN Bin2,CHAIYuanyuan3,QIAOYa’nan1
(1.College of Civil Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China;2.College of Water Conservancy&Environmental Engineering,Zhengzhou University,Zhengzhou 450001,China;3.Gansu Institute of Soil&Water Conservation Sciences,Lanzhou 730020,China)
Abstract:A computer model for simulating unsteady flow in irrigation pipe network was presented in this paper based on the characteristic line(MOC)method.The method established the pipe network structure using branchnode association and node-branch association tables.We discussed how to store,calculate the pipe network data.In the calculation,different types of nodes and pipe network parameters were stored by arrays.As an example,we took the pipe network in spring irrigation and calculated and analyzed the unsteady flow within it.The results showed that the method for storing the pipe network was simple and convenient,and the node types could be identified quickly in calling the subroutine for the boundary condition.The model can be used to simulate and analyze unsteady flow in complicated irrigation pipe network.
Key words:irrigation pipe network;unsteady flow;computer method
中图分类号:TV134.2
文献标志码:A
doi:10.13522/j.cnki.ggps.2017.11.014
石喜,孙斌,柴媛媛,等.灌溉管网非恒定流计算机实现方法[J].灌溉排水学报,2017,36(11):79-85.
文章编号:1672-3317(2017)11-0079-07
收稿日期:2017-04-09
基金项目:国家自然科学基金项目(5109224);兰州交通大学青年科学基金项目(2016018)
作者简介:石喜(1985-),男。副教授,博士,主要从事工程水力学、计算流体力学方面的研究。E-mail:shixi103@163.com
责任编辑:陆红飞