0 引言
水是人类赖以生存和发展的不可替代的一种自然资源，也是维系地球生态平衡、决定环境质量状况最积极、最活跃的自然要素之一[1]。我国是一个干旱缺水的国家，人均可利用水资源少，且时空分布不均匀。自然降水是水资源的主要来源之一，而降水资源的可利用量关乎经济发展和人民生活，可为水资源合理配置研究提供理论依据[2]。因此，研究一个地区的可利用降水资源的变化特征及预测其未来发展情况有着重要的意义。诸多学者针对此问题做了深入研究。例如，基于逐步回归分析法发现西北地区降水量、可利用降水量、年均气温有减少趋势[3]；通过滑动平均和小波分析法发现，1994—2006年淮河流域的可利用降水量呈周期为2～3 a的震荡，浮高、极涡对可利用降水量的影响较大[4]；运用地统计方法、小波分析法和气候趋势系数的方法，宁夏全区可利用降水量自北向南依次增大[5]。目前，多数可利用降水量研究是从区域和流域的角度出发，而对小区域、小地区的研究较少，且大多数研究只是通过趋势分析对研究区域的可利用降水量做了预测分析，并没有对预测结果的可靠性进行检验。
西安，作为丝绸之路经济带和亚欧大陆桥上的重要城市，在“一带一路”建设中占据桥头堡和核心城市的地位。然而，由于人为和自然因素，水资源短缺、水环境问题等一直严重制约着西安的经济发展[6]。因此，有必要对西安1951—2014年均可利用降水量做线性统计分析、趋势和突变分析，并且采用加权马尔科夫链对西安未来可利用降水量做预测。
1 材料与方法
1.1 数据来源
数据来自于中国气象科学共享服务网提供的西安气象数据，包括西安1951—2014年的年平均降水量、逐月平均降水量和逐月平均气温等数据。在计算前，对数据的完整性、一致性进行检验，确保数据的真实性、准确性和可靠性。
1.2 研究方法
1.2.1 可利用降水量的计算
从气象的角度考虑，一个地区的可利用降水量可以表示为降水量减去蒸发量。计算蒸发量（E）的方法有很多，目前大多数学者采用高桥浩一郎公式[7-9]计算可利用降水量，该式采用月平均降水量（P）和月平均气温（T）对月蒸发量进行估算，操作简单、方便，应用广泛且适用于我国北方地区。
1.2.2 可利用降水量趋势和突变分析
Mann-Kendall法被大多数人认为是一种理论基础和应用效果较好的方法，其被世界气象组织推荐并广泛应用于降水、径流、气温、水质等分析研究[10-11]。Mann-Kendall检验方法属于非参数方法，非参数检验方法亦称无分布检验，其优点是不需要样本遵从一定的分布，也不受少数异常值的干扰，更适用于类型变量和顺序变量，计算也比较简便。兹应用Mann-Kendall法对西安市可利用降水量进行趋势，即：
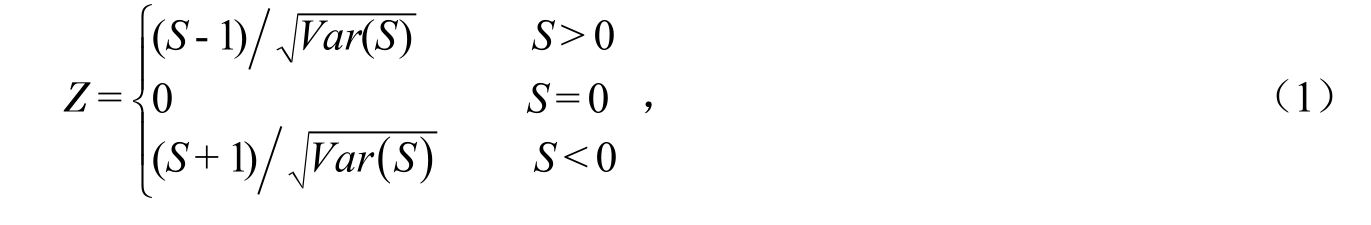
式中：
，其中xi，xj为要检验的随机变量；n为序列长度，sgn(x)为符号函数，当x＞0、x=0、x＜0时，sgn(x)的值分别为1、0、-1；方差 Var(S)=n(n-1)(2n+5)/18。采用双边趋势检验，在给定显著性水平α下，当统计量
时，表示趋势不显著；否则趋势显著，即
表明序列呈显著上升趋势，
表明序列呈显著下降趋势。
突变分析采用有序聚类法[12]，其基本思想是将时间序列看作是一个整体，然后将其分割，根据同类之间离差平方和最小，不同类之间离差平方和最大的原则，找出最优的分割点就是突变点，突变点前离差平方和和突变点后离差平方和的总和（Sn）最小的点即为突变点(τ)。
1.2.3 可利用降水量预测模型的建立
加权马尔科夫链预测模型被广泛应用在降水量预测中，且预测精度较高[12-14]。兹采用滑动平均加权马尔科夫链模型对西安市可利用降水量进行预测，该模型预测方法和步骤为：
1）建立分级标准，确定各年可利用降水量状态。设可利用降水量序列为X1,X2,…,Xn，对可利用降水量序列采用3 a滑动平均处理，采用均值-标准差分级法,将各年滑动平均可利用降水量分为枯水年、偏枯年、平水年、偏丰年和丰水年5个状态（对应于马尔科夫链的5个状态空间）。
2）时间序列马氏性检验。用fij(i，j∈E)来表示转移频数矩阵的元素，即指标值序列X1，X2，…，Xn。从状态i经过一步转移到状态j的频数，对状态所得结果进行统计，可以得到频数矩阵（fij）；根据公式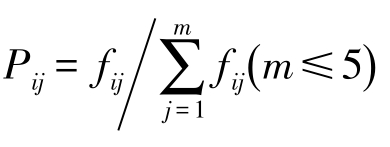
，由概率论知识[15-16]可知，统计量
服从自由度为(m-1)2的χ2分布，其中Pij表示m×m转移概率矩阵。给定显著性水平α，查表可得分位点
值，通过计算得到统计量χ2值。若
，则可认为序列{Xn}符合马氏性，否则认为该序列不可作为马尔可夫链。
3）计算研究序列各阶自相关系数
，式中：rk为第k阶(滞时为k)自相关系数；Xi为第i时段的指标值；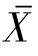
指标值平均值；n为指标值序列长度。
4）对各阶自相关系数规范化。
，式中：m为预测时需要计算到的最大阶数。
5）分别以前面若干时段的指标值为初始状态，结合其相应的各阶转移概率矩阵，即可预测该时段指标值的状态。
6）将同一状态的各预测概率加权和作为指标值处于该状态的预测概率，即
，取max{Pi，i∈E}所对应的状态i为该时段指标值的预测状态。待该时段的指标值确定之后，将其加入到原序列之中，再重复步骤1～6步，即可进行下时段指标值状态的预测。
7）根据预测状态确定准确的预测值。由于采用马尔科夫链预测模型仅能得到一个预测区间，而不能得出预测的准确值，本次研究采用状态特征值结合线性插值的方法来解决这个问题[17]。首先计算状态特征值
其中β＞0为调整因子。然后计算指标值
，其中i为预测状态；Bi、Ti分别为预测区间的下限和上限；k=0，表示状态值与指标值增加趋势一致，k=1则表示其增加趋势不一致。
2 西安可利用降水量特征分析
2.1 可利用降水量线性统计分析
利用西安市1951—2014年逐月平均降水数据和气温数据，采用高桥浩一郎公式计算西安市逐月平均可利用降水量数据。西安市1951—2014年平均年可利用降水量为146.09 mm，可利用降水量最多的年份为1983年，为395.30 mm，该年降水量也是最多的，为903.20 mm；最少年份为1995年，为33.58 mm，该年降水量也是最少的，为312.20 mm。西安市降水量最大值是最小值的2.89倍，而可利用降水量最大值是最小值的11.77倍，可见可利用降水量的多少不仅仅取决于降水量的大小。
图1为西安市年平均可利用降水量变化趋势图。由图1可知，西安市年均可利用降水量一直处于多年的上下波动中，整体趋势呈递减趋势，这与西安市年平均降水量的变化趋势基本一致。3 a滑动平均可利用降水量变化趋势与可利用降水量趋势一致，呈减小趋势，变化幅度相对于年可利用降雨量有所减小。
西安市可利用降水量年内分布很不均匀，月可利用降水量最大值在9月，为40.35 mm；最小值出现在12月，为0.78 mm。年内可利用降水主要集中在夏季（6、7、8月）和秋季（9、10、11月），其中夏季占全年比例为33.4%，秋季占全年的46.4%；而春季（3、4、5月）和冬季（12、1、2月）占全年比例偏小，分别为18.1%和2.1%。
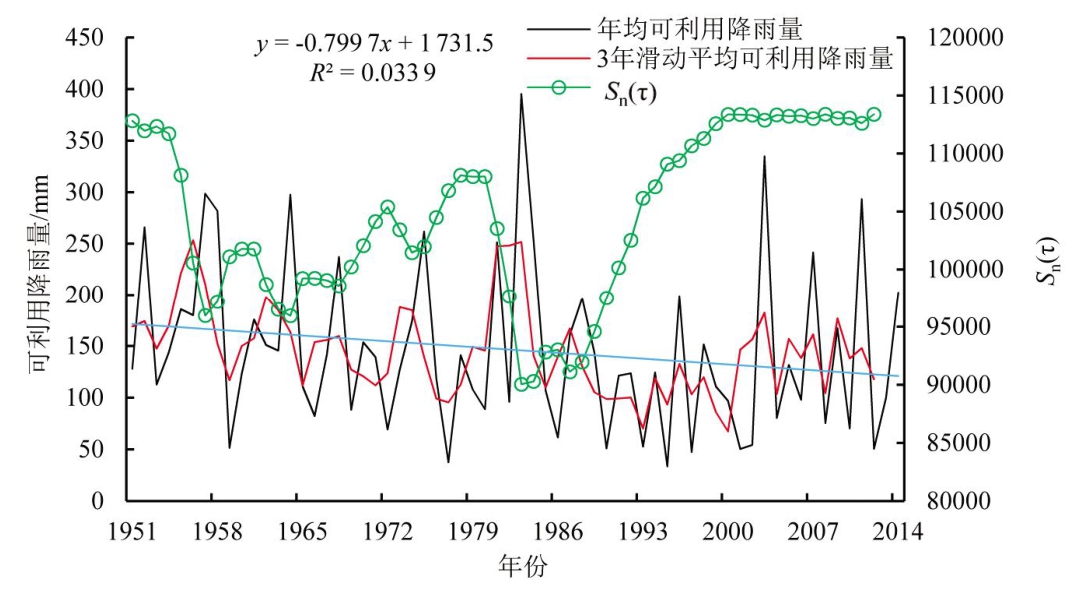
图1 西安年可利用降水量变化趋势及突变检验
2.2 趋势分析和突变分析
由于线性趋势检验不能明确表示出序列的趋势显著性，进而采用Mann-Kendall检验法进行趋势分析，得到西安市年均可利用降水量的Z值为-1.998，表示可利用降水量呈下降趋势，当Z的绝对值大于1.96时，表明该检验通过了0.05显著性水平的显著性检验，其结果与线性趋势分析结果一致。
采用有序聚类法对可利用降雨量序列进行突变分析，计算结果见图1。可以看出1983年的离差平方和最小，说明在1983年可利用降雨量发生突变；1957、1964、1974年为局部较低点，说明在这些年份可利用降雨量也有一定的突变。有学者对西安市降雨量进行了突变分析[13]，其结果与计算可利用降雨量突变年份基本一致，说明可利用降雨量的突变情况主要受到降雨量变化的影响。
3 可利用降水量预测模型
3.1 西安市可利用降水量序列及分级
考虑到降水本身特性及序列数据的结构合理性,根据均值-标准差分级法将滑动平均可利用降水量序列分为5类，分类情况见表1。根据分级标准[2]，确定各年滑动平均可利用降水量的状态。经检验，滑动平均可利用降水量降水序列χ2=40.44，通过了显著水平α=0.05的
检验，因此滑动平均降水量序列具有马氏性，可以使用该方法进行预测。
表1 3 a滑动平均可利用降水量分级
3.2 模型检验
应用1951—2010年滑动平均可利用降水量序列及其相应的概率转移矩阵对2011年的滑动平均可利用降水量进行预测；根据1951—2011年滑动平均可利用降水量序列及其相应的概率转移矩阵对2012年滑动平均可利用降水量进行预测。模型预测结果见表2，预测值和实际值的相对误差分析结果见表3，其中P3a，预测表示3 a滑动平均预测值，P3a，实际表示3 a滑动平均实际值，P预测表示年预测值，P实际表示年实际值。
表2 模型验证及预测结果
表3 预测结果误差分析
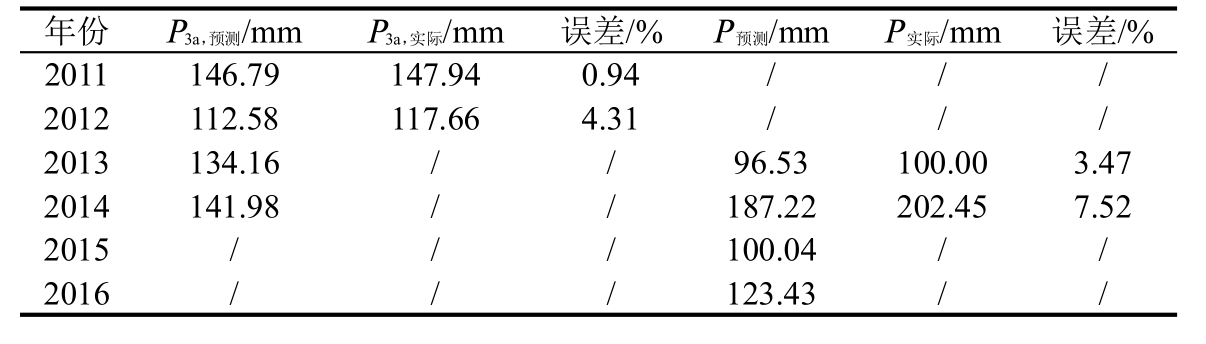
由表2及表3可知，2011年预测状态为状态3，其年滑动平均实际值为147.94 mm，也为状态3，预测结果与实际结果一致，采用状态特征值与线性插值法，取β=1.15，经计算2011年滑动平均预测值为146.79 mm，相对误差为0.94%。根据2011年的3 a滑动平均预测值推算2013年的可利用降水量为96.53 mm，相对误差为3.47%，满足精度要求。2012年预测状态为状态2，其年滑动平均实际值为117.66 mm，也为状态2，预测结果和实际结果一致，采用状态特征值与线性插值法，取β=1.15，经计算2012年可利用降水量滑动平均预测值为112.58 mm，相对误差为4.31%，根据2012年的3 a滑动平均值推算2014年的可利用降水量为187.22 mm，相对误差为7.52%，满足精度要求。由此可见，采用加权马尔科夫链模型及选取的线性插值调整因子（β=1.15）对西安市可利用降水量预测是可行的。
3.3 模型预测
采用西安市1951—2012年的滑动平均可利用降水量序列及其相应的概率转移矩阵，对2013年滑动平均值进行预测，由此可以得出2015年的年可利用降水量，结果见表3；把2013年的预测状态加到实测序列中，采用新的序列并计算其概率转移矩阵，对2014年滑动平均值进行预测，由此可以得出2016年的可利用降水量，结果见表3。
由表2及表3可知，2013年滑动平均可利用降水量为状态3，应用状态特征值与线性插值法得2013年滑动平均值为134.16 mm，结合2013年可利用降水量和2014年可利用降水量可以求得2015年的可利用降水量为100.04 mm；将2013年滑动平均值加入序列中，重复计算得2014年滑动平均值，2014年滑动平均可利用降水量为状态3，根据状态特征值与线性插值法求得2014年滑动平均值为141.98 mm，结合2014年和2015年的可利用降水量，求得2016年可利用降水量为123.43 mm。
4 结论与讨论
1）统计分析表明，西安市可利用降水量年际变化明显，呈多年丰枯交替变化；对可利用降雨量进行3 a滑动平均，其总体变化趋势有所缓和，对其做线性拟合，拟合直线斜率为-0.799，表明可利用降雨量平均每年以0.799 mm的趋势减少。可利用降水量年内随变化主要受季节影响，可利用降雨主要集中在夏秋二季，分别占总量的33.4%和46.4%，其中9月平均量最多，为40.35 mm；春季和冬季可利用降水较少，分别为18.1%和2.1%，其中1月平均量最小，为0.78 mm。
2）采用Mann-Kendall检验法对西安市可利用降水量进行趋势分析，得到Z值为-1.998，表示可利用降水量呈下降趋势，且通过了0.05显著性水平的显著性检验，其结果与线性趋势分析结果一致；有序聚类法突变检验结果表明，西安市可利用降水量在1957年、1964年、1974年和1983年发生突变，其中1983年为突变最明显的年份；该地区可利用降雨量突变结果与降雨量突变结果基本一致，可见可利用降雨量主要受到该地区降雨量变化的影响。
3）采用均值-标准差分级法建立分级标准，对西安市1951—2012年的3 a滑动平均可利用降水量值进行分类，对此序列进行了马氏性检验，建立了滑动平均加权马尔科夫预测模型，并通过2011年和2012年的准确值对模型进行了验证，验证结果误差较小，表明模型具有一定的可靠性。通过建立的预测模型对西安市2015年和2016年可利用降水量进行了预测，预测结果为2015年可利用降水量为100.041 mm，2016年为123.43 mm。
滑动平均加权马尔科夫模型是一个简单方便、结果合理、精度较高的预测方法，应用此模型可以依据现有的降雨资料预测未来几年的可利用降雨量，可以为当地的水资源合理利用提供依据，给当地水资源调配方案的建立提供参考。该模型的不足之处在于其只能确定出预测年所处的状态，即其预测值是一个状态区间，而不能得到一个准确值，为了得到较准确的预测值还需要结合其他方法来确定，文中采用状态特征值与线性插值法确定预测结果的准确值，得到的结果误差较小，但是其中调整因子的确定方法及该方法在其他地区的适用性还需进一步研究。
参考文献：
[1]徐恒力.水资源开发与保护[M].北京：地质出版社，2001.
[2]吴健华，李培月，钱会.西安市气象要素变化特征及可利用降雨量预测模型[J].南水北调与水利科技，2013，11(1):50-54.
[3]吴立君，葛朝霞，曹琨，等.西北地区可利用年降水量趋势分析及预测[J].人民黄河，2011,33(12):51-55.
[4]宋颖玲，葛朝霞，曹琨，等.淮河流域可利用降水量特征及其影响因子分析[J].水电能源科学，2010,28(3):4-5.
[5]徐利岗，汤英，杜历，等.近58年来宁夏可利用降水量多时间尺度变化特征分析[J].灌溉排水学报，2012,31(2):85-90.
[6]李斌，解建仓，胡彦华，等.西安市近60年降水量和气温变化趋势及突变分析[J].南水北调与水利科技，2016,14(2):55-61.
[7]高桥浩一郎．根据月平均气温、月降水量推算蒸散量[J].天气(日文)，1979,26(12)：759-763.
[8]付菁，范广洲，周定文.高桥公式在拉萨地区的适用性及其修正[J].应用气象学报，2012,23(2)：231-237.
[9]雷雨，龙爱华，邓铭江，等.1926—2009年额尔齐斯河流域中游地区气候变化及其对水资源的影响分析[J].冰川冻土，2012,34(4)：912-919.
[10]霍正文，陈文，凡炳文.近54年定西市降水趋势及突变分析[J].水文，2012,32(3):88-92.
[11]CLAUDIA Libiseller.A program of multivariate and partial Mann Kendall test[R].Sweden:University of LinkÖping,2002.
[12]王涛，钱会，李培月.加权马尔可夫链在银川地区降雨量预测中的应用[J].南水北调与水利科技，2010,8(1):78-81.
[13]文彦君.基于权马尔可夫链的宝鸡市年降水量状态预测[J].中国农学通报，2012，28(26):272-276.
[14]黄华，蔡仁，穆振侠，等.基于模糊集修正加权马尔科夫模型在新疆降水预测中的应用[J].新疆农业科学，2015,52(10):1 891-1 898.
[15]汪荣鑫.数理统计[M].西安：西安交通大学出版社，2006.
[16]刘建民.随机过程[M].西安：西北大学出版社，2003.
[17]钱会，李培月，王涛.基于滑动平均-加权马尔科夫链的宁夏石嘴山市年降水量预测[J].华北水利水电学院学报，2010,31(1):6-9.