表1 土壤基本物理指标

颗粒量/%黏粒7.29粉粒62.31砂粒30.4质地分类粉壤土干体积质量/(g·cm-3)1.45田间持水率(体积)/%34.2凋萎系数/%13.2
陈俊克1,2,缴锡云1,2,庄 杨3,郭维华1,2
(1.河海大学水利水电学院,南京210098;2.河海大学水文水资源与水利工程科学国家重点实验室,南京210098;3.常州市城市防洪工程管理处,江苏常州213017)
摘 要:利用沧州市南皮生态农业试验站点2011—2013年不同土层深度的含水率及降雨量和降雨时间,结合由植株叶面积指数得到的不同生育期植株的截留容量,分析了最大容水量S和最大降雨强度二者与降雨有效性的相关关系,并在此基础上建立了次降雨有效降雨的估算模型。结果表明,土壤初始含水率与降雨有效性线性相关,且在不发生溢流情况下,可以用土壤最大容水量S作为是否考虑土壤初始含水率折减作用的分界点;另外,对于降雨强度I≥0.7 mm/min的降雨,降雨强度与降雨有效性相关性显著,并且随最大降雨强度的增大,降雨有效性逐渐减小;最后将运用传统模型和新估算模型计算的有效降雨量值与实测有效降雨量值验证对比,新模型比传统模型更加贴近实测有效降雨,并且降雨量较大时差别更加明显。
关 键 词:次降雨;植株截留;降雨强度;初始含水率;有效降雨模型
降雨是补充灌溉的主要水源[1],有效降雨量是制定灌溉制度的重要依据,目前应用较为普遍的关于有效降雨估算的方法有USDA-SCS方法、Hershfield方法和传统的经验估算模型等[2]。但是,USDA-SCS方法和Hershfield方法均是在不考虑土壤种类的情况下建立的,认为对任一地区而言,都可统一取普通类型的土壤、气候和土壤蓄水量的平均数用于估算当地年际有效降雨量,这2种方法针对不同地点的适用性有所限制[3-4]。另外有效降雨的影响因素众多[5],如降水总量、降水强度及历时;气象因素(包括气温、湿度、风速等);土壤质地因素(包括地形、坡度、有机质量等);还有降雨前根系层土壤贮水量、根系深度等,传统的经验估算模型仅把降雨量作为主导因素,对次降雨进行简单的折减计算分析,进而得到有效降雨量,这一过程忽略了许多重要的影响因素,其计算结果不能满足现代精细耕作的要求。
已有研究表明,对于特定的地区而言,降雨前土壤初始含水率、次降雨量、次降雨强度是影响有效降雨量的关键因素[6]。因此,将次降雨强度、土壤初始含水率、作物不同生育阶段的冠层截留对降雨的折减作用均纳入有效降雨量的影响因素范围,结合试验点作物叶面积及叶面积指数、不同土层深度的含水率和相对应年份该站点的降水量和降水时间数据,分析3种因素对次降雨有效性的影响,进而构建新的有效降雨量的估算模型,力求得到一个更精确并相对简便的有效降雨估算方法。
试验于河北沧州中科院南皮生态农业试验站(116°40'E,38°06'N)开展。该地多年平均降水量550 mm,年平均日照时间2 318 h,水面蒸发量为1 900~2 200 mm,地下水埋深5~7 m。选取试验小区以地表为临界点,每10 cm为1层,分10层分别用环刀法测其干体积质量、田间持水率,并取各层土壤约500 g通过全自动激光粒度分析仪测定试验田质地,结果见表1。
表1 土壤基本物理指标

采用2011—2013年南皮生态农业试验站点等8个传感器测取的0~100 cm土层含水率和对应年份该站点的降水量和降水时间数据。将传感器测得土壤水分数据与人工测量数据进行匹配与订正,得到该站点连续3 a的降雨时间、降雨量和降雨强度以及0~20、20~40、40~60、60~100 cm各土层土壤体积含水率。将2011—2013年降雨量和土壤含水率绘制成图,如图1、图2所示。
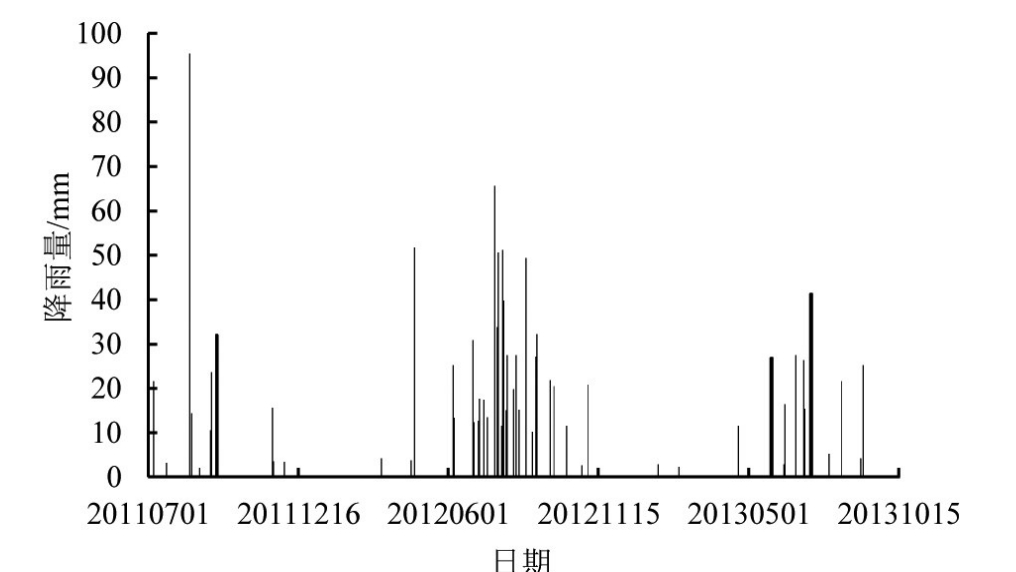
图1 2011—2013年降雨量

图2 2011年8月—2013年9月0~100 cm土层土壤含水率
有效降雨为测得降雨前、后1 m土体储水量差值,采用差减法确定。将0~100 cm土层看作小麦、玉米的根系层[7],土壤含水率超出田间持水率的视为无效降雨。另外将降雨前的土壤含水率视为土壤初始含水率。
植株冠层的测定随机选取试验点3个尺寸为2.5 m×1.75 m的测坑试验小区,测坑四周采用混凝土固化防渗且坡度为0°。冬小麦选用“衡观35”,播种量为300 kg/hm2,即200 g/小区。各小区冬小麦南北方向种植,行距20 cm,中间留出1条观测数据行,每个小区共播种10行。夏玉米选用“郑单958”同样按照南北方向种植,保持行距60 cm,株距25 cm。冬小麦、夏玉米不同生育期均在小区内随机选取20株样本,直尺量测确定单株叶面积,并计算确定叶面积及叶面积指数[8](表2、表3)。
表2 冬小麦不同生育阶段的叶面积指数
表3 夏玉米不同生育阶段的叶面积
国内外学者针对冬小麦和夏玉米在降雨过程中的植株冠层截留已做了大量研究。植物的冠层截流容量是指在降雨过程中,水分经过作物冠层再分配后被保留在作物冠层内的水量,包括茎、叶、穗上的水量[9]。降雨经过植被冠层的再分配作用后被分为4个部分:冠层截留量、茎秆流量、穿透雨量以及冠层内蒸发量[11]。冠层截留容量直接影响到达地表的总雨量。研究[11-12]表明,密植型作物冬小麦的冠层截留容量WI是几乎不受降雨强度的影响,仅与其所处生育阶段的LAI和降雨量相关。降雨强度只对作物冠层截留容量达到饱和的速度有影响。宽行作物夏玉米的冠层截留容量CI会随降雨强度的增加而增加,其值与叶面积和降雨强度关系较为密切。根据二者构建的冬小麦冠层截留容量WI、夏玉米冠层截留容量CI与降雨强度I、LAI、AL之间的关系模型,以及小区试验实测的冬小麦LAI值与夏玉米的AL值,可分别计算冬小麦和夏玉米冠层截留容量。
冬小麦[11]:

夏玉米[12]:
![]()
式中:WI为冬小麦冠层截流容量(mm);LAI为叶面积指数(无量纲);P0为降雨量(mm);CI为夏玉米冠层截留容量(mm);AL为植株叶面积(m2);I为降雨强度(mm/min)。
根据冬小麦冠层截留容量关系模型,由表2中冬小麦不同生育阶段叶面积指数和梯度为10、20、30、40、50、60 mm的降雨量P0最终分析得到冬小麦不同生育阶段对应降雨折减量,返青期、拔节期、抽穗期、灌浆—成熟期冠层截留容量分别为0.71、1.09、1.66、1.63 mm。另外,对于某一场降雨而言,夏玉米的冠层截留容量CI虽与降雨强度有很大关联,但其冠层截留容量必定存在一个饱和值,根据不同梯度雨强和作物所处不同时期叶面积,确定不同生育阶段冠层截留容量饱和时对应的降雨强度:三叶期为20 mm/h,拔节期为40 mm/h,抽雄期、开花期、抽丝期、灌浆期、乳熟期均为50 mm/h。由此得到夏玉米不同生育阶段对应降雨折减量,三叶期、拔节期、抽雄期、开花期、抽丝期、灌浆期、乳熟期冠层截留容量分别为1.33、3.11、4.09、4.22、4.31、4.32、4.27 mm。
选用SCS法产流计算模型[13-14]分析土壤初始含水率对降雨有效性的影响。

式中:Q为地表径流量(mm);S为最大容水量(mm),没有实测土壤含水率的情况可根据美国水土保持局提出的公式S=25 400/CN-254进行粗略估算,CN取值见表4;F为累计下渗量(mm);Ia为初损值(mm)。
在总降雨量相同的情况下,Ia在作物某一生育阶段可以视为定值,径流量Q与最大容水量S成反比,Q随S的增大而减小。因为土壤初始含水率直接影响CN取值,所以判定土壤初始含水率直接影响次降雨的地表径流量与累计下渗量。由于不同的土壤初始含水率会影响降雨过程的径流量Q,考虑到畦埂对入畦降雨的围阻作用,因此分析土壤初始含水率对次降雨有效性的影响时,重点关注发生蓄满产流的情况。
对于实测资料而言,即便次降雨的降雨量相同,但是很难保证降雨过程相同,为了分析土壤初始含水率对降雨有效性的影响,假定选取的降雨过程对有效降雨的影响可忽略不计。将2011—2013年降雨资料有效降雨量与总降雨量的比值λ和土壤初始含水率θi绘制成散点图进行回归分析,结果见图3。
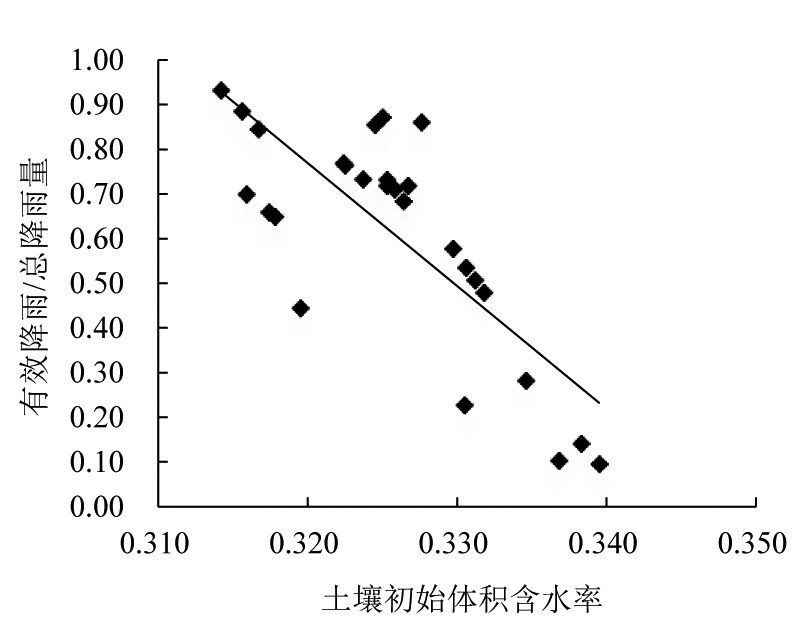
图3 土壤初始体积含水率与有效降雨/总降雨量的相关分析
由图3可知,次降雨的有效性随土壤初始含水率的增高而显著降低,回归方程为:
土壤初始含水率与降雨有效性的相关系数R=0.779,n=27,P<0.002,可知土壤初始含水率和降雨有效性显著相关。
SCS产流计算模型中选取CN值的土壤状态划分标准,将次降雨前5 d的降雨总量对土壤湿度进行划分。根据SCS模型对土壤的分类标准,沧州地区的土壤属于C类(黏壤土、薄层沙壤土、有机质量低或黏质量高的土壤,最小渗透率为1.27~3.81 mm/h),对于不同雨前湿度的土壤根据美国水土保持局的CN值换算表[15-16],罗列对应S见表4。
表4 根系层土壤3种状态的划分

对于不发生降雨溢出畦田的次降雨而言,以雨前土壤某一状态的最大容水量S作为是否要考虑土壤初始含水率折减作用的分界点。首先根据雨前5 d的水量划分土壤状态,然后根据作物冠层截流作用后的降雨量与最大容水量大小,确定有效降雨量。即:
式中:Y为作物冠层截留容量;其余符号意义同上。
实际降雨入渗过程中,有效降雨的大小一般会受入渗速率的影响。降雨强度I小于相应时刻的入渗速率i时,抵达地表的降雨可以全部入渗到土壤中,此段时间入渗速率等于降雨强度;当某一时刻I≥i时,此时地表水分接近饱和并开始产生径流。此段时间内入渗速率为土壤下渗速率[17]。因此,分析降雨强度对有效降雨的影响十分重要。
研究表明,对于某一种土壤而言,在土壤体积质量、孔隙度、有机质量均不发生显著变化时,随入渗进行到一定时间后,入渗速率i趋于一稳定值,该值相当于地表含水率θ0的导水率K(θ0),其值小于土壤的饱和导水率KS。根据阮芯竹等[18]研究成果计算KS值,即:
式中:KS为土壤的饱和含水率(10-3cm/s);Z为土层深度(cm)。试验选取KS为0.7 mm/min,并通过降雨资料对I<0.7 mm/min进行检验,结果表明I<0.7 mm/min的降雨过程对降雨有效性不产生影响。
由于短时间的大雨强并不会引发降雨漫出畦埂,所以考虑大雨强对应的有效系数k时要综合考虑最大雨强对应的降雨历时,选择总降雨量较大的降雨分析大雨强对应的有效降雨系数,其中大雨强对应的有效系数k为有效降雨与折减后总降雨量比值,即k=P/P´。选取发生雨强I≥0.7 mm/min的降雨,首先根据降雨发生的日期确定相应植株截流作用Y,将总降雨量实测值和相对应时期的植株折减雨量作差求得折减后总降雨量P´,即P´=P0-Y。再根据实测的土壤根系层贮水量资料选取相应的土壤最大滞留量S,对不同雨强(I)与有效降雨/折减后总降雨量(P/P´)进行相关分析,P/P´=2.091 6I-0.269,R2=0.735 2。
其中降雨强度与有效降雨/折减后总降雨的相关系数R=0.857,n=9,P<0.005,表明降雨强度与降雨有效性相关性显著。随降雨强度增强,次降雨的有效性降低。相应的大雨强有效降雨系数k见表5。
表5 大雨强情况下的有效降雨系数
将作物截流作用Y、作物根系层最大容水量S、大雨强造成的超渗产流现象对应的有效降雨系数k,分别依次纳入影响次降雨有效性的因素。考虑到作物根系层对水分有一定的容量,对于总降雨量小于30 mm的降雨,计算有效降雨量时只考虑植株的截流作用。对于降雨量大于30 mm的降雨在计算有效降雨P时,应将植株折减的降雨量Y和雨前土壤初始含水率选取相应的S值均考虑在内。对于降雨过程中发生I>0.7 mm/min且总降雨量超过30 mm的降雨,如果降雨历时时间长,则通常情况下P=S,如果降雨历时短且集中,则需要在考虑作物冠层截流容量Y与对应的土壤最大容水量S后,再用k进行折减。即:

式中:I为降雨强度(mm/min);P为有效降雨量(mm);k为大雨强对应的有效降雨系数。
作物不同生育阶段、雨强土壤初始含水率以及最大降雨强度对应的有效降雨估算表见表6。
由表7可知,实测有效降雨量一般都低于有效降雨模型计算值,并且传统有效降雨模型与实测有效降雨偏差较大。比较传统模型和新模型可知,当降雨量相对较小时,二者与实测有效降雨量差别相对较小,新模型相对优于传统模型;当降雨量偏大时,传统模型计算值与实测有效降雨量差别较大;而新模型差别较小。
表6 有效降雨估算结果

注“—”代表此时间段内处于作物种植阶段,不考虑冠层截留作用,根据前5 d的来水情况判断对应的S值。
根据实测降雨量和有效降雨量运用沧州地区使用的传统模型和构建后的新模型分别计算,结果见表7。
表7 有效降雨量实测值和模型计算值对比

1)土壤初始含水率与降雨有效性线性相关。并且根据次降雨前5 d来水总量划分土壤湿度状态用以确定土壤的最大容水量S。对于不发生溢流的次降雨,可以用雨前土壤最大容水量S作为是否考虑土壤初始含水率折减作用的分界点,即当P0-Y<S时,P=P0-Y;当P0-Y≥S时,P0=S。
2)对于I<0.7 mm/min的降雨,降雨过程对降雨有效性不产生影响;对于I≥0.7 mm/min的降雨,降雨强度与降雨有效性相关性显著,并且随最大降雨强度的增大,降雨有效性逐渐减小。
3)传统有效降雨模型计算较大降雨量的有效降雨时,其计算值与实测有效降雨量差别较大,而新模型更加接近实测有效降雨量。对比传统模型与新模型计算结果可知,当降雨量偏小时,二者与实测有效降雨量差别小,新模型优于传统模型;当降雨量偏大时,新模型计算降雨量与实测有效降雨量差别小,新模型明显优于传统计算模型。
兹分析了作物截留、初始含水率、降雨雨强对降雨有效性的影响,并提出3个影响因子对次降雨有效性的折减作用表,得到了估算有效降雨的新模型。与传统模型对比,新模型按照实际情况对不同降雨适用的有效降雨系数进行更细致、全面的划分。与以往研究的USDA-SCS方法、Hershfield方法做对比,新模型更加直观、简便。新模型的建立更精确并可以相对简便地估算得到有效降雨,更好地解决了现代精细耕作的部分问题。另外,文中所采用数据是根据南皮生态试验站2011—2013年实测资料所得,年限较短,结果存在局限性,需要进一步扩大观测年份,得到更长年限的数据,对各影响因子的折减作用进行验证;实测资料很难实现单因子分析,需进一步通过人工降雨的方式对本文研究结论进行检验。
参考文献:
[1]TAFTEH A,SEPASKHAH A R.Application of HYDRUS-1D model for simulating water and nitrate leaching from continuous and alternate furrow irri gated rapeseed and maize fields[J].Agricultural Water Management,2012,113(10):19-29.
[2]PATWARDHAN A S,NIEBER J L,JOHNS E L.Effective rainfall estimation methods.[J].Journal of Irrigation&Drainage Engineering,1990,116(2):182-193.
[3]刘战东,段爱旺,肖俊夫,等.旱作物生育期有效降水量计算模式研究进展[J].灌溉排水学报,2007,26(3):27-30.
[4]杨燕山,陈渠昌,郭中小,等.内蒙古西部风沙区耕地有效降雨量适宜计算方法[J].内蒙古水利,2004(1):67-70.
[5]李粉婵.山西省小麦、玉米依靠降雨满足作物需水程度的分析[J].山西水利科技,2005(1):21-23.
[6]ARNAUDP,BOUVIERC,CISNEROSL,etal.Influenceofrainfallspatialvariabilityonfloodprediction[J].JournalofHydrology,2002,260(1-4):216-230.
[7]李峰,缴锡云,李盼盼,等.田间土壤水分特征曲线参数反演[J].河海大学学报(自然科学版),2009,37(4):373-377.
[8]段爱旺.作物群体叶面积指数的测定[J].灌溉排水学报,1996(1):50-53.
[9]马波,李占斌,马璠,等.模拟降雨条件下玉米植株对降雨再分配过程的影响[J].生态学报,2015,35(2):497-507.
[10]刘海军,康跃虎,王庆改.作物冠层对喷灌水分分布影响的研究进展[J].干旱地区农业研究,2007,25(2):137-142.
[11]刘战东,刘祖贵,秦安振,等.麦田降雨入渗特征及其计算模型[J].水土保持学报,2014,28(3):7-13.
[12]郑子成,李廷轩,张锡洲,等.模拟降雨条件下玉米植株对降雨再分配的作用[J].水土保持研究,2012,19(4):72-76.
[13]陆海平,陈红姣.降雨对粘性土路堑边坡含水状态的影响[J].路基工程,1998(2):16-21.
[14]KUROSU T,FUJITA M,CHIBA K.Monitoring of rice crop growth from space using the ERS-1 C-band SAR[J].IEEE Transactions on Geoscience&Remote Sensing,1995,33(4):1 092-1 096.
[15]GUZZETTI F,PERUCCACCI S,ROSSI M,et al.The rainfall intensity–duration control of shallow landslides and debris flows:an update[J].Land slides,2008,5(1):3-17.
[16]DOLTRA J,MUÑOZ P.Simulation of nitrogen leaching from a fertigated crop rotation in a Mediterranean climate using the EU-Rotate_N and Hydrus-2D models[J].Agricultural Water Management,2010,97(2):277-285.
[17]CLAPP R B,HORNBERGER G M.Empirical equations for some soil hydraulic properties[J].Water Resources Research,1978,14(4):601-604.
[18]阮芯竹,程金花,张洪江,等.重庆市四面山不同土地利用类型饱和导水率[J].水土保持通报,2015,35(1):79-84.
Investigating Effective Rainfall and FactorsAffecting Effective Rainfall Using Experiments and Modelling
CHEN Junke1,2,JIAO Xiyun1,2,ZHUANG Yang3,GUO Weihua1,2
(1.College of Water Conservancy and Hydropower Engineering,Hohai University,Nanjing 210098,China;2.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering,Hohai University,Nanjing 210098,China;3.The Management Office of the City Flood Control Engineering in Changzhou,Changzhou 213017,China)
Abstract:This paper analyzed the maximum holding capacity of water by soil,rainfall intensity and effective rainfall(portion of a rainfall staying in root zone)based on rainfalls and soil water content profiles measured at Nanpi Agro-ecological Experimental Station in Cangzhou from 2011 to 2013.The interception of rainfalls by canopy at different growing periods was calculated using leaf area and leaf index.A quantitative relationship between the effective rainfall and rainfall was proposed.The results showed that the initial soil water content was linearly correlated to the effective rainfall.In the absence of surface runoff,the maximum holding capacity of water by soil could be used as a threshold of whether a reduction in initial water content should be considered.In addition,when rainfall intensity was higher than 0.7 mm/min,the correlation between rainfall intensity and effective rainfall was significant,and with the increase in maximum rainfall intensity,the effective rainfall decreased.Comparing the effective rainfall calculated using the traditional model and the proposed model with the measured results showed that the proposed model was more accurate,especially for large rainfalls.
Key words:rainfall;interception by canopy;rainfall intensity;initial soil water content;effective rainfall model
中图分类号:S161.6
文献标志码:A
doi:10.13522/j.cnki.ggps.2017.04.003
文章编号:1672-3317(2017)04-0015-06
责任编辑:白芳芳
陈俊克,缴锡云,庄杨,等.次降雨有效降雨量的影响因素及其估算模型[J].灌溉排水学报,2017,36(4):15-20.
收稿日期:2016-11-23
基金项目:水利部公益性行业专项经费项目(201301014)
作者简介:陈俊克(1992-),男,河南周口人。硕士研究生,主要从事灌溉排水理论与技术研究。E-mail:141302060017@hhu.edu.cn
通信作者:缴锡云(1962-),男。教授,博士生导师,博士后,主要从事节水灌溉理论与技术研究。E-mail:xyjiao@hhu.edu.cn