张 伟1,何武全1,2
(1.西北农林科技大学 水利与建筑工程学院,陕西杨凌 712100;2.旱区农业水土工程教育部重点实验室,陕西杨凌 712100)
摘 要:针对试算法工作量大、计算误差大和精度低等问题,建立了以计算流量和设计流量之差最小为目标函数的抛物线形渠道断面优化数学模型,将粒子群优化算法引入到抛物线形渠道断面优化计算中,采用粒子群算法在全局空间下搜索渠道断面优化问题的全局最优解。并以陕西省石头河灌区五丈源支渠抛物线形混凝土渠道为例,对其二次抛物线形渠道断面的方程形状参数a和设计水深h进行了优化设计。结果表明,得到满足约束条件的最优方程形状参数a为5.06,最优设计水深h为0.398 2 m。与原设计相比模型计算所得渠道过水断面面积减少了0.102 1%,渠道土方量减少了6.225 4 m3,混凝土衬砌量减少了4.764 1 m3,工程占地面积也随之减少。粒子群优化算法能有效地解决抛物线形渠道断面设计中的优化问题,且具有收敛速度快、计算精度高和全局寻优能力强等优点。
关 键 词:抛物线形渠道;断面优化;粒子群算法
在农业水利工程中,渠道是一种主要的输水建筑物,多年实践经验表明,采用渠道防渗技术能够减少70%~90%的输水损失[1],因此建设安全可靠的输配水渠系,设计合理最优的渠道断面形式,对提高农业灌溉用水的有效利用率和发展我国节水农业具有十分重要的意义。渠道断面有各种各样的形式,在灌溉事业发展的早期,为了便于施工和保持渠道边坡的稳定,梯形断面成了当时最常用的形式,但梯形渠道渠口宽度大,占地面积大,在防冻胀能力上不能满足一定的工程要求,在通过大量的实验证明后,出现了许多新型的渠道断面结构形式,主要有U型、弧形底梯形、弧形坡脚梯形等。近几年,随着施工机具的发展,抛物线形渠道由于其方程的连续性在施工、制模中更容易计算和控制,在我国北方寒冷地区也开始推广应用,和U型渠道比,其优点主要是断面连续性好,抗冻胀效果更好,模具制作更容易计算和控制等。
渠道断面的优化设计直接关系着渠道工程的经济性、水资源利用效率以及其在农业生产中所发挥的效益。传统的渠道断面优化设计方法有试算法、图解法等,往往计算量大、重复工作多且计算精度易受设计人员的主观影响。随着计算机技术和人工智能技术的日益发展,国内外专家学者开始将多维、非线性的算法引入到渠道设计中,并取得了一系列研究成果,如利用遗传算法全局搜索的优点将渠道断面的设计概化为数学优化模型的方法来解决设计中的优化问题[2];建立了包含水力要素与经济要素的多目标优化函数,应用人工蜂群算法在全局空间下搜索渠道断面优化问题的全局最优解[3];引入扩展微分进化算法建立流量误差最小的目标函数,有效解决了渠道断面的优化设计问题[4];在满足混凝土衬砌渠道冻胀要求下建立了最优水力断面和工程造价最小的目标函数,利用自适应粒子群算法对混凝土衬砌梯形渠道断面结构进行了优化[5];将免疫遗传算法应用于河北省怀来县洋河二灌区渠道改造中对其梯形横断面的底宽及设计水深等参数进行了优化设计[6];应用待定的拉格朗日乘数法选取抛物线形底三角形截面渠道的最佳横断面,在经济上更加优化[7];考虑渗流损失、蒸发损失、土地购置成本以及内壁和开挖成本等方面因素应用拉格朗日乘数法解决了水平底抛物线形面渠道优化模型[8];基于渗漏损失和工程费用最小提出明渠断面优化模型,应用FORMPGSL方法优化渠道设计[9];应用遗传算法和序列二次规划方法对三角形、矩形和梯形截面渠道进行了优化设计[10]。然而,这些研究多是针对梯形、U型等断面渠道的优化设计,而对于新型的抛物线形渠道的优化设计相对较少。因此,有必要建立以计算流量和设计流量之差最小为目标函数的抛物线形渠道断面优化数学模型,将粒子群算法首次引入到抛物线形渠道断面优化设计问题中,并验算该算法的有效性,在考虑抛物线形渠道断面最优的基础上,兼顾渠道工程占地最小、混凝土衬砌量最小,以陕西省石头河灌区五丈塬支渠抛物线混凝土渠道计算为实例,计算优化结果。
抛物线形渠道断面的优化设计是在糙率n、渠道底坡i已知的条件下,使设计流量与计算流量之差最小和渠道过水断面的面积最小,同时需要满足一定的约束条件,在这些约束条件下计算出抛物线形渠道形状参数a和渠道水深h的最优解。以计算流量Q和设计流量Qd为目标函数,则有:
渠道断面为抛物线形,如图1所示,抛物线方程为y=ax2。设a为方程形状参数,b为水面宽,h为渠道正常水深。根据明渠均匀流公式计算过水流量[11-13],明渠均匀流基本公式为:
式中:Q为过水流量;A为过水断面面积,![]() ;χ为湿周,
;χ为湿周,![]() ;i为渠道底坡;n为糙率。
;i为渠道底坡;n为糙率。
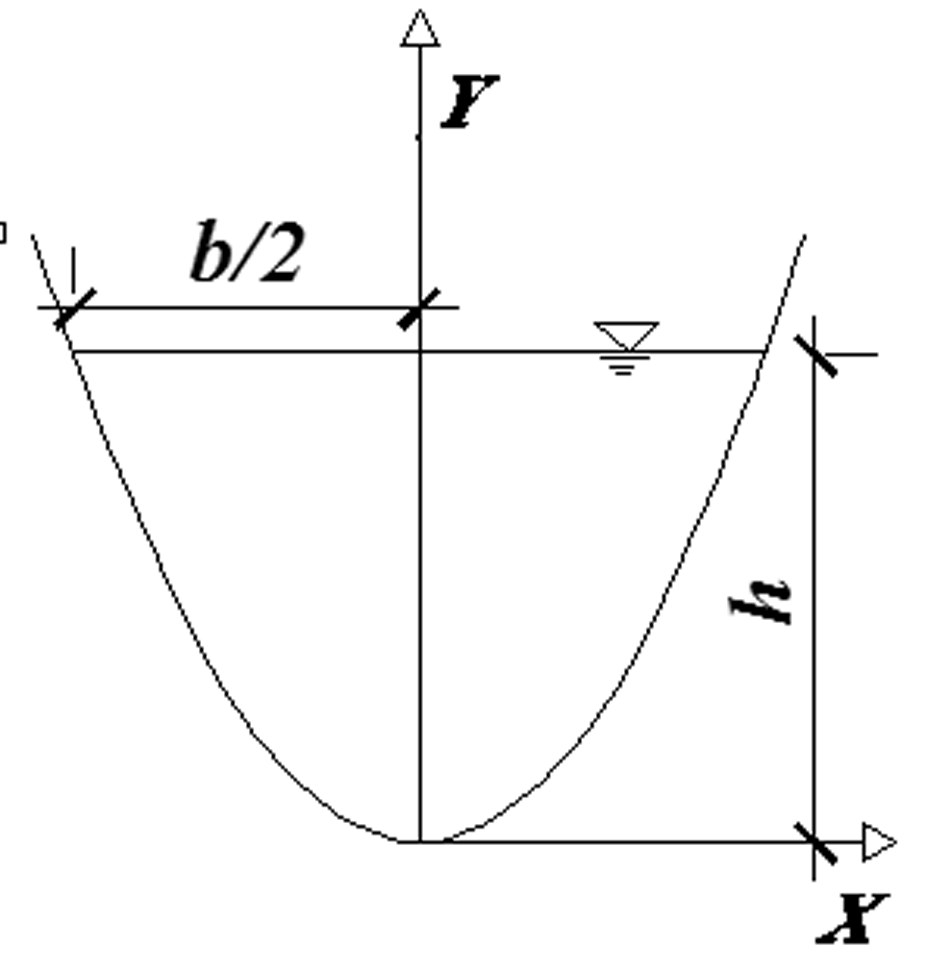
图1 渠道断面示意图
则有二次抛物线形渠道流量与水深的关系,即:
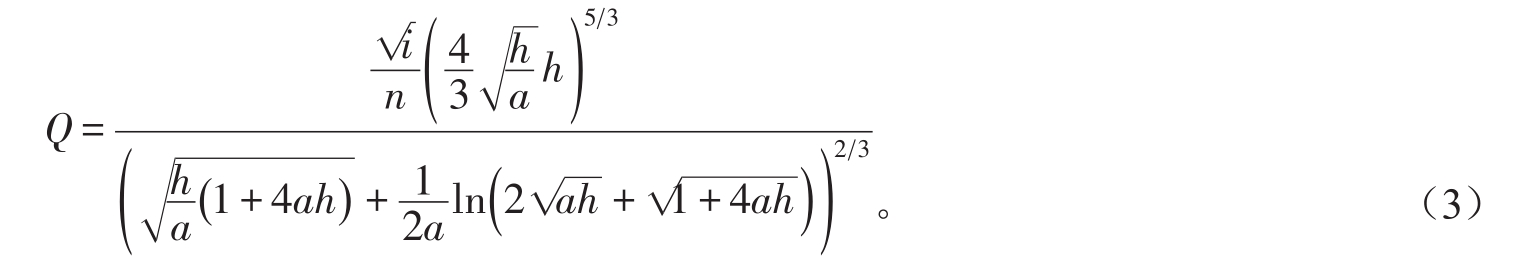
可得二次抛物线形渠道断面优化模型为:
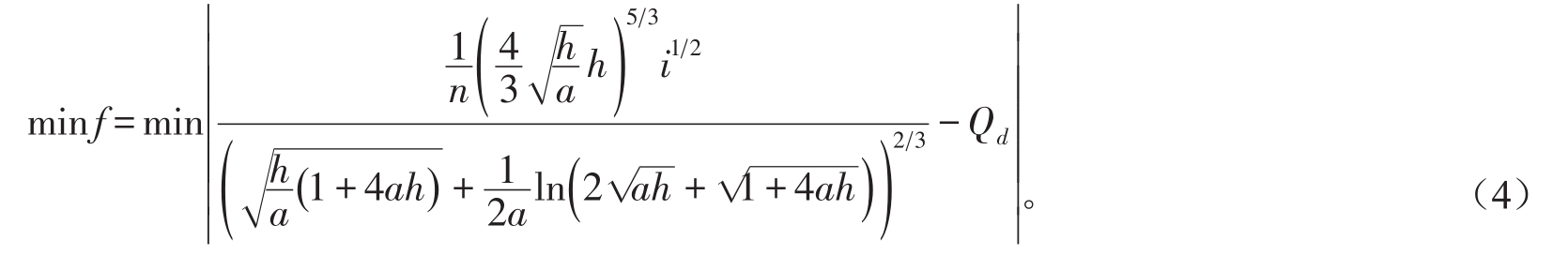
考虑到工程设计及渠道稳定性要求,目标函数的约束条件[15-16]为:
1)流速约束:渠道流速应满足不冲、不淤要求,平均流速应介于不淤流速和不冲流速之间,其中不淤流速为vcd,不冲流速为vcs,即![]()
2)渠道宽深比:渠道宽深比应满足:0.8<b/h<3.5。
粒子群优化算法(Particle Swarm Optimizer,PSO算法)[14-15]是源于对鸟群捕食行为的研究而提出的一种新型全局优化算法。在PSO算法中,每个优化问题的潜在解都是搜索空间中的一只鸟,称之为“粒子”,所有的粒子都有一个被优化的函数决定的适应值,每个粒子还有一个速度决定他们飞翔的方向和距离,然后粒子们就追随当前的最优粒子在解空间中搜索,PSO算法首先初始化一群随机粒子即随机解,然后通过迭代找到最优解。假设在一个d维搜索空间中的第i个粒子的位置和速度分别为Xi=(xi,1,xi,2,…,xi,d)和Vi=(vi,1,vi,2,…,vi,d),在每一次迭代中,粒子通过跟踪2个最优解来更新自己,第一个就是粒子本身所找到的最优解,即个体极值pbest,Pi=(pi,1,pi,2,…,pi,d);另一个是整个种群目前找到的最优解,即全局最优解gbest,Pg。在找到这2个最优值时,粒子可以根据公式更新自己的速度和新的位置,公式为:
式中:w为惯性权重;c1和c2为正的学习因子;x1和x2为0到1之间均匀分布的随机数。
与其他算法相比,粒子群优化算法收敛速度快,算法简单,容易实现,有记忆能力,对非线性问题具有较强的全局搜索能力,适用于求解复杂的数学模型。
粒子群优化算法在抛物线形渠道断面的优化设计中的应用首先需要对参数进行初始化,把形状参数a和渠道水深h作为设计变量,计算目标函数,最后利用粒子群优化算法对设计变量以及目标函数进行寻优,其具体寻优过程为:
第一步:初始化粒子群中粒子的位置和速度。
第二步:计算每个粒子的适应度值,将其位置和适应值存储在各粒子的pbest中,寻找粒子的最优值和位置存储在gbest中。
第三步:利用式(5)和式(6)更新粒子的速度和位移。
第四步:对每个粒子,用它的适应值与其经历过的最好位置作比较,如果较好,则定其为当前的最好位置。
第五步:比较当前所有的pbest和gbest,更新gbest。
第六步:若满足停止条件(通常为预设的运算精度或迭代次数),搜索停止,输出结果,否则返回第三步继续搜索。
选取陕西省石头河灌区五丈源支渠抛物线形混凝土渠道为研究对象,该渠道选择在五丈源支渠(0+200~4+200)段实施,该渠段原为U型渠道,其设计口宽56 cm,渠深50 cm,设计水深40 cm,渠道底坡0.012 5,设计流量0.33 m3/s,混凝土衬砌厚度为5 cm。在改造为抛物线形混凝土渠道的过程中,渠道底坡i为0.012 5,糙率系数n取0.014,渠道不冲流速vcs为5.0 m/s,渠道不淤流速vcd为0.23 m/s,采用传统计算方法,仍然选取设计水深为40 cm,通过试算法可以确定满足设计流量要求下的抛物线形方程形状参数a以及计算流量Q,如表1所示。
表1 流量试算结果
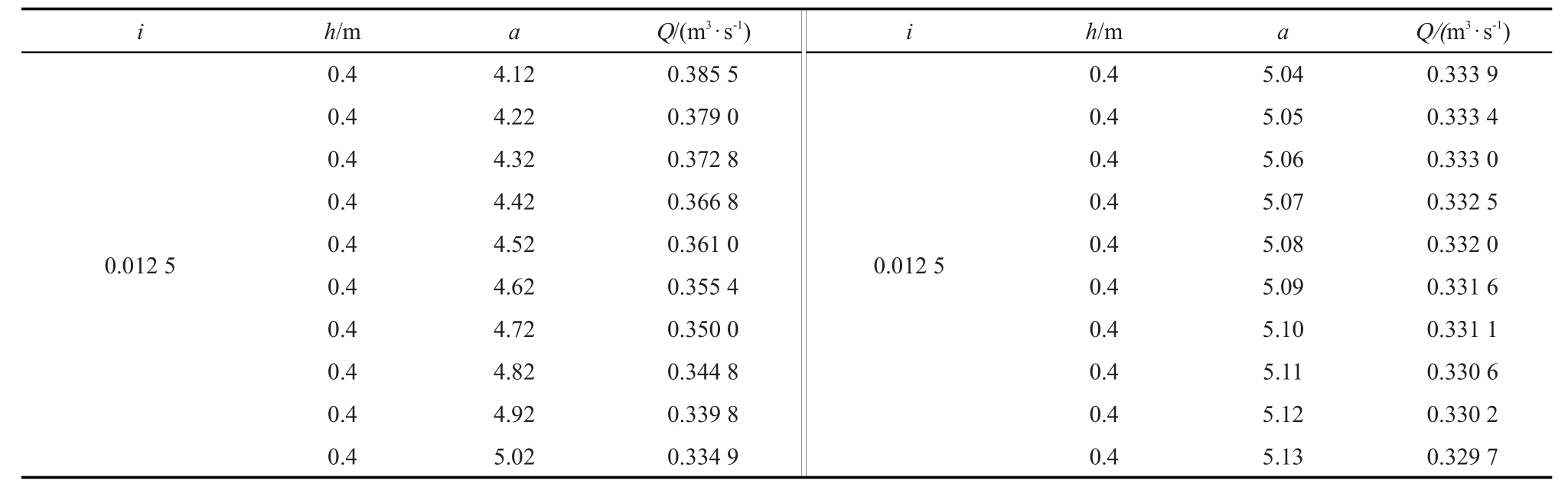
由表1可知,选取抛物线方程系数a=5.12,设计流量为0.33 m3/s,抛物线方程式为y=5.12x2。现利用粒子群优化算法求解,建立以计算流量与设计流量之差最小为目标函数,并以不冲不淤流速为约束进行全局搜索,以寻求最能满足抛物线形渠道设计的形状参数a和水深h。则目标函数为:
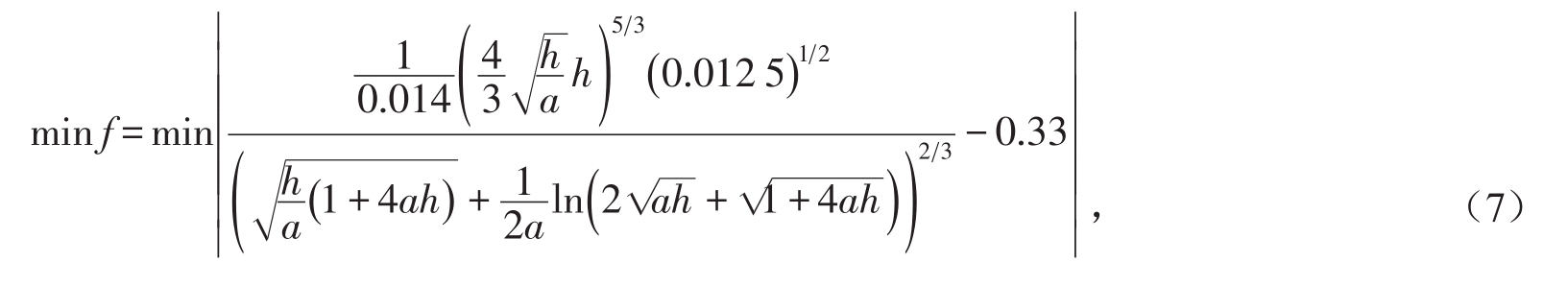
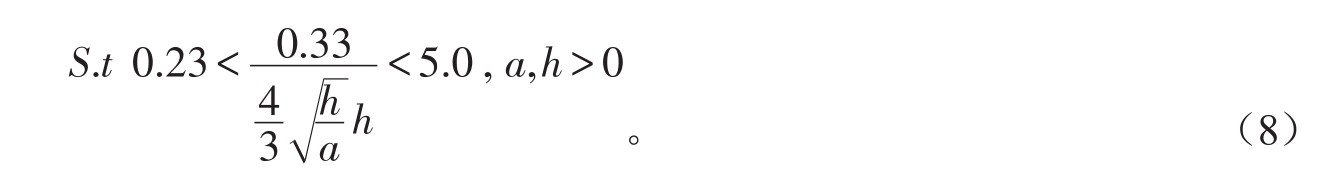
本实例中粒子群优化算法参数设置为:进化次数为500,种群规模为200,学习因子c1、c2都为1.494 45,优化变量a取离散值区间[5.00,5.20],优化变量h初始变化区间取[0.0,1.0],实例中的约束条件采用罚函数形式处理,则粒子群搜索结果与试算法结果如表2所示。
表2 粒子群搜索结果与试算法结果
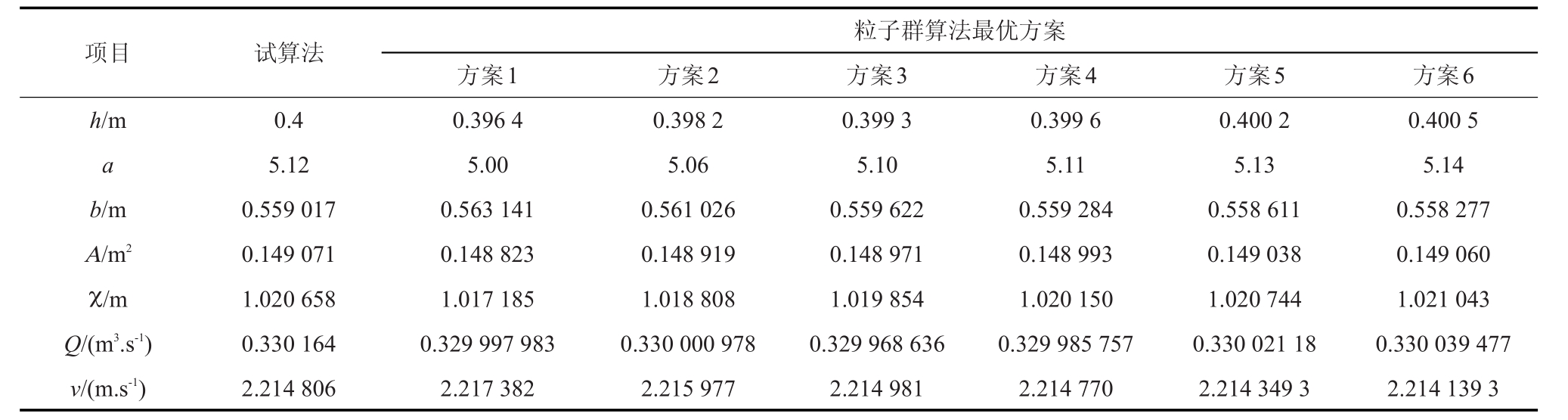
由表2可知,粒子群优化算法经过20~30次的全局搜索提供了多个最优组合,且都满足约束条件,结果精度达到10-7m3/s,一定程度上克服了传统优化方法的缺点。抛物线方程形状参数a的不同对渠道断面优化有一定影响,a取5.06时过水断面面积最优,比试算法中a取5.12时过水断面面积减少了0.102 1%,在计算流量与设计流量相当接近的情况下可以减少渠道工程的开挖量,在对试算法和最优化方案所得抛物线形渠道土方量对比分析发现,最优化方案即a取5.06,h取0.398 2 m时,抛物线形渠道土方量减少了6.225 4 m3,抛物线形渠道混凝土衬砌量减少了4.764 1 m3,表明该优化断面以及粒子群优化算法能够满足抛物线形渠道工程优化设计要求。
1)粒子群算法作为一种高效的全局优化算法,对于农田水利工程设计中的非线性问题的求解具有很强的适应性,与渠道设计中的一般优化方法相比,收敛速度快、求解精度高、通用性强,并且能够得到最优结果。因此粒子群算法在农田水利工程设计中有着广泛的应用前景。
2)应用粒子群算法对陕西省石头河灌区五丈源支渠抛物线形混凝土渠道断面进行了优化设计,构建了以设计流量与计算流量之差最小的优化模型,在糙率和渠道底坡已知的条件下,计算抛物线形渠道形状参数a和渠道水深h的最优解。计算结果表明,在满足一定约束条件下,抛物线形渠道方程形状参数大小在渠道断面优化问题上有一定影响,选择合适的二次抛物线形方程即a为5.06时,渠道过水面积减少了0.102 1%,渠道土方量减少了6.225 4 m3,抛物线形渠道混凝土衬砌量减少了4.764 1 m3,在实际的工程施工中能够有效地减少占地面积,为抛物线形渠道混凝土衬砌厚度的设计提供了参考依据,具有工程实际意义。
参考文献:
[1]张晨笛,何武全,张希栋,等.季节性冻土地区渠道防渗防冻胀新材料及应用[J].水资源与水工程学报,2011,22(5):145-148.
[2]鲍卫锋,黄介生,孔祥元,等.基于遗传算法的渠道断面最优设计[J].中国农村水利水电,2005(5):75-76.
[3]钱坤,苏国韶.人工蜂群算法在渠道断面优化设计中的应用[J].水利水电科技进展,2011,31(3):57-60.
[4]倪士超,迟道才.基于扩展微分进化算法的渠道断面优化设计[J].人民长江,2009,40(13):81-82.
[5]刘东,胡宇祥,付强,等.北方灌区混凝土衬砌渠道断面优化及参数分析[J].农业工程学报,2015,31(20):107-114.
[6]郭凤台,侯毅凯,杨丽,等.免疫遗传算法在洋河二灌区渠道优化设计中的应用[J].农业工程学报,2007,23(3):85-87.
[7]BABAEYANKOOPAEI K,VALENTINE E M,SWAILES D C.Optimal Design of Parabolic-Bottomed Triangle Canals[J].Journal of Irrigation&Drainage Engineering,2000,126(6):408-411.
[8]DAS A.Optimal Design of Channel Having Horizontal Bottom and Parabolic Sides[J].Journal of Irrigation&Drainage Engineering,2007,133(2):192-197.
[9]ADARSH S.Modeling Qarametric Uncertainty in Optimal Open Channel Design Using FORM-PGSL Coupled Approach[J].Stochastic Environmental Research&RiskAssessment,2012,26(26):709-720.
[10]KENTLI A,MERCAN O.Application of Different Algorithms to Optimal Design of Canal Sections[J].Journal of Applied Research&Technology,2014,12(4):762-768.
[11]何武全,宋清林,宋江涛,等.抛物线形混凝土衬砌渠道标准化结构形式研究[J].灌溉排水学报,2016,35(5):14-18
[12]吕宏兴,裴国霞,杨玲霞.水力学[M].北京:中国农业出版社,2002:167-174.
[13]张志昌,刘亚菲,刘松舰.抛物线形渠道水力最优断面的计算[J].西安理工大学学报,2002,18(3);235-237.
[14]GB/T50600-2010.渠道防渗工程技术规范[S].
[15]脱云飞,王克勤,宋维峰,等.灌溉渠道优化设计方法研究[J].中国农村水利水电,2012(4):58-60.
[16]龚纯,王正林.精通MATLAB最优化计算[M].北京:电子工业出版社,2014:270-312.
[17]张国华,张展羽,邵光成,等.基于粒子群优化算法的灌溉渠道配水优化模型研究[J].水利学报,2006,37(8):1 004-1 008.
Optimizing Channels with Parabolic Cross-Section Using the Particle Swarm Method
ZHANG Wei1,HE Wuquan1,2
(1.College of Water Resources andArchitectural Engineering,NorthwestA&F University,Yangling 712100,China;2.The Ministry of Education Key Laboratory of Agricultural Water and Soil Engineering,Yangling 712100,China)
Abstract:A mathematical model for optimizing channels with parabolic cross section was developed in this paperin attempts to resolving the problems such as high computation demanding,low accuracy associated with the trial-error method used in the conventional method.The objective in the optimization was to minimize the difference between the calculated flow rate and designed flow rate,and the optimal solutions were solved by particle swarm algorithm assuming that the cross section of the channel is Parabolic.We took the concrete channel in Wuzhangyuan branch in the Stone River Irrigation District of Shaanxi province as an example,and the equation shape parameter(a)and the design depth(h)of the second parabolic channel section were designed optimally.The results showed that a,which met the constraints,was 5.06 and h was 0.398 2 m.Compared to the original design,the cross section,the volume of the channel and the concrete lining quantity reduced by 0.102 1%,6.225 4 m3and 4.764 1 m3,respectively.Therefore,the particle swarm optimization algorithm can effectively solve the optimization of parabolic channel and has the advantages of fast convergence,high accuracy and more efficient in searching the global optimization solution.
Key words:parabolic channel;cross section optimization;particle swarm algorithm
中图分类号:TV91
文献标志码:A
doi:10.13522/j.cnki.ggps.2017.04.017
文章编号:1672-3317(2017)04-0094-05
责任编辑:刘春成
张伟,何武全.基于粒子群算法的抛物线形渠道断面优化方法[J].灌溉排水学报,2017,36(4):94-98.
收稿日期:2016-09-16
基金项目:国家“十三五”重点研发课题(2016YFC0400203)
作者简介:张伟(1991-),男,安徽安庆人。硕士研究生,研究方向为水工结构设计理论与材料。E-mail:2369161851@qq.com
通信作者:何武全(1967-),男,陕西合阳人。副教授,主要从事节水灌溉理论与技术研究。E-mail:hewuquan1967@sina.com