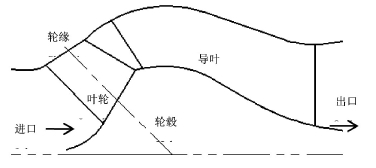
图1 斜流泵流道图
徐瑛丽
（浙江同济科技职业学院， 杭州 311231）
摘 要：以比转速为392的斜流泵为研究模型，选取叶片出口安放角、叶片出口边宽度、后盖板倾角3个参数作为研究变量，采用CFD方法对斜流泵性能进行了多参数组合优化的数值计算，并根据性能试验数据验证了CFD数值方法的准确性。基于Box-Behnken试验建立3因素3水平共17组叶轮模型的试验表并对各方案设计工况下的内流进行了数值计算。采用二次响应面模型拟合效率的性能预测模型，给出目标函数，基于遗传算法对目标函数进行求解。结果表明，对效率影响最为显著的参数为叶片出口安放角，其次为叶片的后盖板倾角，且效率均随二因素的增大而减小，叶片出口边宽度对其影响最小；与原模型叶轮叶片参数相比，β2、b2大于原模型参数，T2保持不变，优化结果显示模型泵水力效率提高1.2%，扬程提高了0.8%。
关键词：斜流泵；叶片参数；Box-Behnken试验；组合优化
斜流泵是一种高比转速的叶片泵，其性能和结构介于离心泵和轴流泵之间，兼具二者的优点，广泛应用于排洪、排污、农田排灌、核电站、制冷等领域。一直以来斜流泵的性能研究都是水力机械行业的热点问题。近年来，诸多学者[1-3]致力于开发出性能更优的混流泵模型。国外，以减少导叶内部损失最优化目标，基于加权平均代理模型对高比转速混流泵导叶进行了优化设计，最终使混流泵效率在设计工况点提升了7.05%[4]。国内，对混流泵叶片进行优化，提高了泵扬程和效率[5-6]；借鉴汽轮机叶片设计方法，运用NUMECA对叶片径向几何参数进行优化设计，较大地提高了混流泵的性能[7]；通过改变叶片数，同时以效率和扬程为优化目标，对叶片进口边形状、叶片前缘厚度和叶片厚度变化规律进行优化，最终使混流泵效率提高到90.6%，空化余量降低了45%[8]；随着间隙的增大，引起效率下降，由于叶片的有效翼展减小，扬程和功率也会有所下降[9]；研究了混流泵叶片安放角对性能的影响，并提出了相应的统计公式[10]。目前，鲜有学者将叶轮叶片多参数进行组合优化。为此，基于试验测试，采用Box-Behnken试验设计法和多元非线性回归分析，拟合斜流泵性能预测方程，综合分析叶轮叶片参数对斜流泵性能的影响，为斜流泵的性能预测和优化提供一定指导。
以比转速为392的斜流泵作为研究对象。该泵流量Qopt为1 300 m3/h，扬程H为16 m，转速n为1 450 r/min。叶轮主要参数为平均外径（D2）、叶片数（z）、叶轮出口宽度（b2）、后盖板倾角（T2）、叶片进口安放角（β1）和叶片出口安放角（β2），其值分别为320 mm、5片、91 mm、18°和18°，流道图如图1所示。
图1 斜流泵流道图
对于定常、不可压缩流体，雷诺时均方程可表示为：
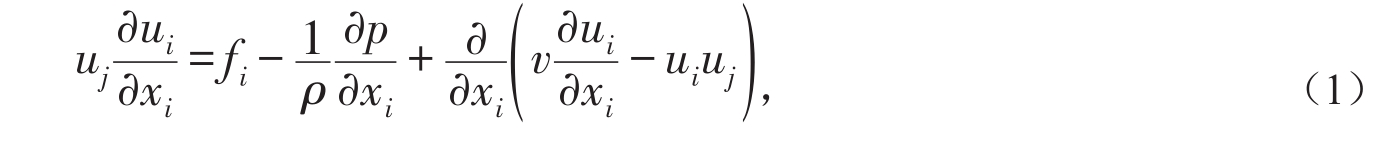
式中：ui代表与坐标轴xi平行的速度分量，i=1,2,3；为流体所受i方向的单位质量力；ρ为流体密度（kg/m3）；p为压力（Pa）；v为运动黏度（m2/s）。SST模型考虑了湍流主剪切应力输运的影响，其湍动能k和比耗散率ω的输运方程表达式为：
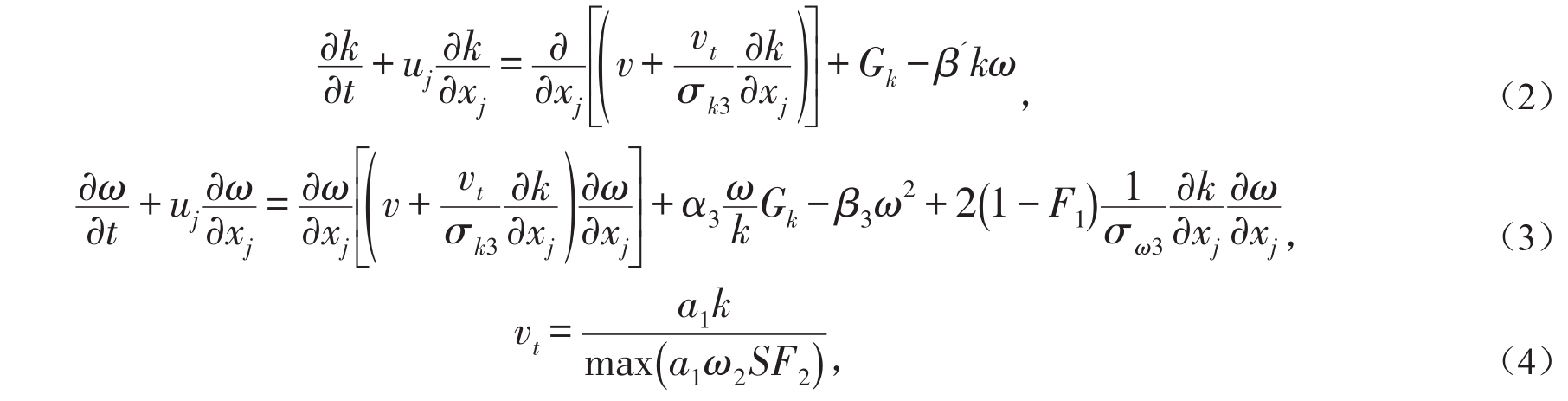
式中：vt为湍动黏性系数，vt=μt/ρ；F1为加权函数；F2是用于约束存在不合适假设的自由剪切流的限制数；S为应变率的定估计值；σk3、Gk、β′、∂3、β3、σω3、a1、w2为经验参数。
利用CFX15.0对斜流泵进行全流场定常数值计算，湍流模型均采用SST湍流模型，计算0.8Qopt、0.9Qopt、Qopt、1.1Qopt和1.2Qopt共5个工况点。计算域共包括4部分：进口延长段、叶轮水体、导叶水体及出口延长段，进口边界条件设置为压力进口，为101 325 Pa；出口边界条件为质量流量出口。斜流泵叶轮、导叶、吸入室等各零部件的壁面都设为固壁条件，壁面边界满足无滑移条件，壁面设置粗糙度为0.05 mm。叶轮设置为旋转区域，转速为1 450 r/min，其余区域设置为静止区域；动静区的交界面采用冻结转子交界面（Fronzen rotor interface）。计算的收敛精度设置为10-4。斜流泵的水力效率（ηh）计算公式为：
容积效率(ηv)估算公式为：
机械效率(ηm)估算公式为：
总效率(η)的计算公式为：
式中：ρ为流体密度（kg/m3）；Q为流量（m3/h）；H为扬程（m）；M为流体对转轴的力矩（N/m）；ω为旋转角速度（rad/s）；ns为比转速。
表1 网格无关性检查
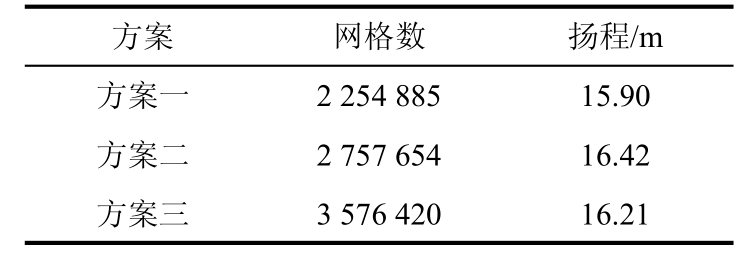
利用ICEM15.0网格划分软件对水体进行非结构四面体网格划分。表1为网格无关性检查结果。设置3组密度不同的网格方案，其网格质量均达到0.2以上，精度满足CFD计算要求，对比3组方案计算得到的扬程预测值，其中方案一网格扬程预测值与方案二相差3.25%，而方案二网格与方案三扬程偏差仅有1.3%。考虑计算精度与计算成本，最终选择方案二。
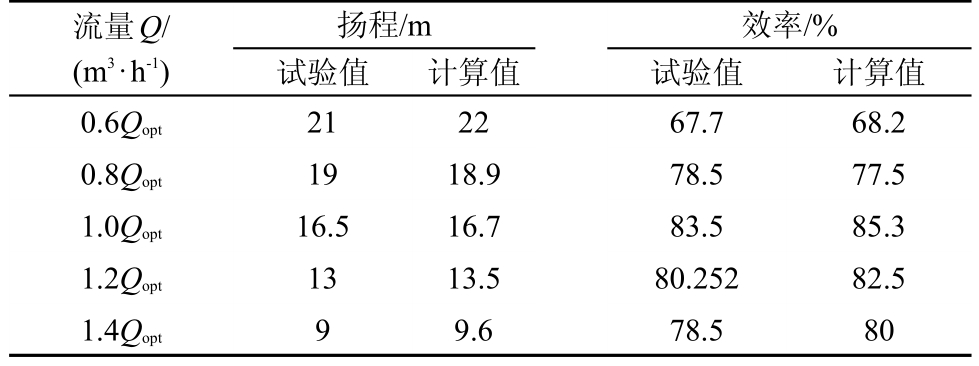
模型泵外特性试验与数值计算对比结果如表2所示。从表2可以看出，试验与数值计算的扬程、效率曲线变化趋势基本一致，扬程均随流量增大而减小，效率随流量的增大先升高后降低，Qopt工况下，扬程的计算值与试验值误差最低，仅1.3%，效率的误差为1.8%，其余工况的数值计算值与试验值误差均在5%以内，这表明计算误差在允许范围内，数值计算方法较为准确。
表2 不同工况下扬程和效率试验值与计算值对比结果
Box-Behnken试验设计方法为响应面试验设计法的一种，其试验点的位置为各水平的中点位置，因此在因素相同时，该试验设计法试验次数最少，在满足试验要求的前提下，选用该方法可节约成本，提高效率。兹采用Box-Behnken试验设计方法将不同参数水平组合成不同方案，并对各方案进行数值计算，为建立叶轮关键参数与泵效率的多元线性关系式提供足够样本点，进而探求叶轮关键参数对斜流泵性能的影响。
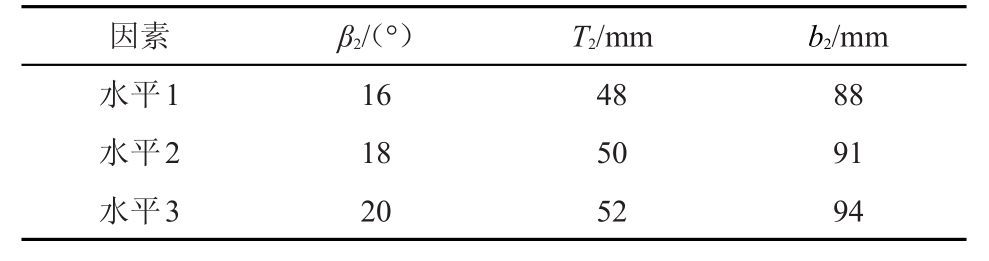
本次优化建立在比转速基本不变的前提下，综合考虑到斜流泵的实际使用要求及不改变原叶轮室，因此保持原叶轮进出口直径不变，且与同一个导叶装配，选取叶轮叶片的3个因素，即β2、b2、T2，将每个因素设置为3水平，如表3所示，其中水平2和水泵原型参数一致。
表3 因素水平设置
Box-Behnken设计方法的特点就是有重复试验，便于分析试验误差，例如方案2、方案7、方案8、方案9、方案17。Box-Behnken设计试验次数N=2k（k-1）+c0，其中k表示因素数，c0表示中心试验点的重复数，用以检验试验误差，兹采用Box-Behnken试验设计法共设计17组试验方案及数值计算，结果如表4所示。
表4 Box-Behnken试验方案及结果
将表4数据作为斜流泵性能预测模型的输入参数，采用二次响应面法拟合出斜流泵性能预测模型。二次响应面模型是最常用的近似模型。其数学表达式为：
式中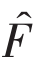
(x)为近似值；xi为设计变量因素；n为变量因素的个数；a0、bi、cij和di分别为各项式的待定系数。采用复相关系数(R2)检验响应面模型生成模型的拟合精度高低，R2越接近于1，表明响应面的拟合精度越高。
借助仿真软件，以效率为目标，基于拟合出的二次响应面模型，求解式（9）中各项系数，从而得到目标函数为：
依据二阶响应面近似模型的拟合精度评价准则，得到复相关系数R2=0.995，由此看来，此响应面模型近似程度较好。图2为各因素与效率的关系曲线，曲线越陡表明因素对效率的影响越大。从图2可以看出，3个因素对效率的影响由大到小依次为：β2、T2、b2，η随β2、T2的增大而减小，随b2的增大先缓慢增大再缓慢减小，近似呈抛物线关系。
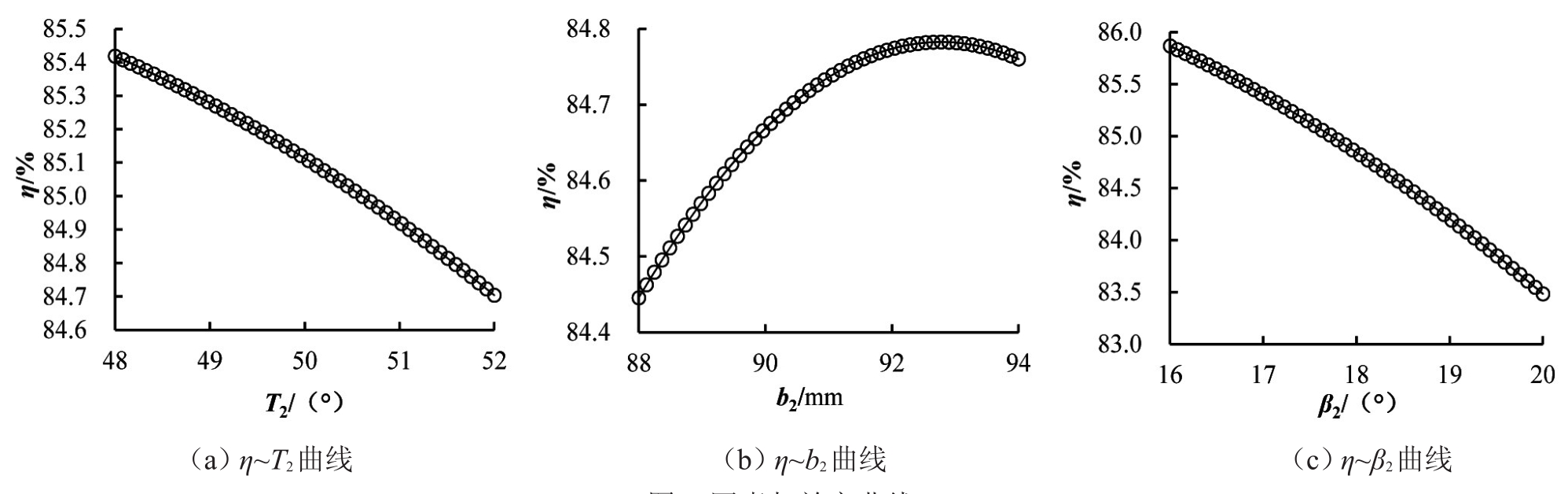
图2 因素与效率曲线
遗传算法是仿生类算法的代表，是最常用的优化算法之一，其模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象，在每次迭代中都保留1组候选解，并按某种指标从解群中选取较优的个体，利用遗传算子（选择、交叉和变异）对这些个体进行组合，产生新一代的候选解群，重复此过程，直到满足某种收敛指标为止。
兹使用传统遗传算法对目标函数进行求解，遗传算法的种群规模及最大优化代数分别设为60和40，交叉概率设为100%。考虑到种群的多样性和搜索效率，将变异概率设为3%，步骤如图3所示。
基于Matlab遗传算法工具箱，定义-Y=f，f=myfit(x)。
fitness Function=@myfit;
nvars=3;
options=gaoptim set;
options=gaoptim set(options,'PopulationSize',60);
options=gaoptim set(options,'CrossoverFraction',1);
options=gaoptim set(options,'M igrationFraction',0.03);
options=gaoptim set(options,'Generations',40);
[X,FVAL]=ga(fitnessFunction,nvars,options)。
经过适应度函数40代进化，得出最优解β2=17°、T2=50°、b2=92 mm，与原模型叶轮叶片参数相比，β2、b2大于原模型参数，T2保持不变，最终得到的优化方案数值计算结果为：η=86.2%，H=16.53 m，结果显示与原模型泵相比，水力效率提高1.2%，扬程提高0.8%。
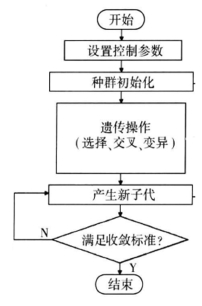
图3 优化流程图
采用CFD方法对比转速为392的斜流泵性能进行了多参数组合优化的数值计算，基于Box-Behnken试验结果，以叶轮关键参数为自变量，以效率为因变量，建立二阶响应面近似模型，复相关系数达到0.995，表明近似模型拟合精度良好，所研究的叶轮的3个关键因素对效率的影响程度由大到小依次为β2、T2、b2，效率与β2、T2负相关，与b2正相关；使用遗传算法对基于二阶响应面模型构建的目标函数进行求解，将求解出的最优方案与原模型对比，结果表明，β2取值小于原模型，T2与原模型一致，b2大于原模型参数；本次优化将模型泵设计工况下水力效率提高了1.2%，扬程提高了0.8%，表明斜流泵叶轮多参数组合优化有效，可为流体机械的优化研究提供指导。
参考文献：
[1]HEO M W,KIM K Y,KIM J H,et al.High-efficiency design of a mixed-flow pump using a surrogate model[J].Journal of Mechanical Science and Technology,2016,30（2）：541-547.
[2]KIM J H,AHN H J,KIM K Y.High-efficiency design of a mixed-flow pump[J].Science in China Series E:Technological Sciences,2010,53（1）：24-27.
[3]KIM J H,CHOI J H,HUSAIN A,et al.Performance enhancement of axial fan blade through multi-objective optimization techniques[J].Journal of Me chanical Science and Technology,2010,24（10）：2 059-2 066.
[4]KIM J H,KIM K Y.Optimization of vane diffuser in a mixed-flow pump for high efficiency design[J].International Journal of Fluid Machinery and Systems,2011,4（1）：172-178.
[5]LU Jinling,XI Guang,QI Datong.Optimization method on impeller meridional contour and 3D blade[J].Chinese Journal of Mechanical Engineering-English Edition,2007,20（6）：43-49.
[6]BING Hao,CAO Shuling.Experimental study of the influence of flow passage subtle variation on mixed-flow pump performance[J].Chinese Journal of Mechanical Engineering,2014,27（3）：615-621.
[7]贾瑞宣，徐鸿．低比转数混流泵叶轮优化设计[J].排灌机械工程学报，2010,28（2）：98-102．
[8]王巍，陆鹏波，王晓放，等．混流泵叶片优化及基于状态方程模型的空化研究[J].大连理工大学学报，2013,53（1）：29-35．
[9]钱涵欣，何成连，刘丽艳．固定导叶安放角及轮缘间隙对混流泵性能影响的研究[J].水力发电，1997（4）：36-38.
[10]何希杰，劳学苏，李平双．混流泵叶片角对性能的影响[J].水泵技术，2005（6）：15-16.
Multi-parameter Optimizing the Impellers in Mixing-flow Pump
XU Yingli
（Zhejiang Tongji Vocational College of Science and Technology,Hangzhou 311231,China）
Abstract：Using the mixing-flow pump 392 as an example,and taking outlet width of the blade,dip angle of the back shroud,outlet angle of the blade as optimization variables,we analyzed the performance of mixing-flow pump using multi-parameter optimization and CFD simulation.The CFD model were verified by energy performance data.Three factors andthree levels were used to calculate the internal flow based on the Box-Behnken experiment.The predicted performance efficiency was fitted using the quadratic response-surface model.The objective function was solved using the genetic algorithm.The results showed that the most significant parameter was outlet angle of the blade,followed by dip angle of the back shroud,and that the efficiency of the pump decreased as the values of these two factors increased;in contrast,the outlet width of the blade had an insignificant effect on the efficiency.The two impeller blade parameters,β2and b2,were larger than those of original model,while T2 remained unchanged.The optimization results showed that the hydraulic efficiency and the head of the model pump could be improved by 1.2%and 0.8%,respectively.
Key words:mixing-flow pump；blade parameters；Box-Behnken experiments；combined optimization
中图分类号：TH311
文献标志码：A
doi：10.13522/j.cnki.ggps.2017.05.014
责任编辑：刘春成
徐瑛丽．斜流泵叶轮的多参数组合优化[J]．灌溉排水学报，2017,36（5）：79-83.
收稿日期：2016-10-12
作者简介：徐瑛丽（1980-），女，山东滨州人。讲师，硕士，主要从事水利工程教学与教改研究。E-mail:xyllyx123321@163.com
文章编号：1672-3317（2017）05-0079-05