李亚斌1,2，徐盼盼1,2，钱 会1,2，王海科1,2
（1.长安大学环境科学与工程学院，西安710054；2.长安大学旱区地下水文与生态效应教育部重点实验室，西安710054）
摘 要：为了全面分析铜川地区降水的时间分布特征，为该区域水资源预测提供依据，基于铜川市1960—2013年年降水量资料，采用样本均值-均方差分组方法，确定了其分级标准及状态，并根据马尔可夫理论，运用统计学原理，验证了该降水序列具有马尔可夫性，建立了适用于该地区的加权马尔可夫链对降水量的预测模型，并根据已有资料验证了预测结果的真实有效性；再结合模糊集理论的级别特征值，对降水量做了具体预测。结果表明，采用1～5阶时间步长预测时，相对误差较小，更符合要求；2014、2015年均为正常年，2014年的降水量为585.82 mm，2015年的降水量为649.21 mm；正常年和偏枯年出现的概率较大，枯水年出现的可能性最小。
关键词：加权马尔可夫链；铜川地区；降水量预测；模糊集理论；遍历性与平稳分布
一直以来，气象条件的复杂性、多样性和不可预知性[1]，对社会发展具有一定的制约作用，尤其表现为降水量的不均匀性和时空分布的不连续性。因此，加强对降水量的预测就显得尤为重要，不仅可以指导当地的农业发展，也可以为当地政府部门的决策提供一定的理论依据。随着马尔可夫理论的不断完善，越来越多的学者开始将马尔可夫链应用于降水量的预测且取得了良好的效果[2-6]。例如，2003年成功地应用加权马尔可夫链预测了降水量的状态；2006年成功地将马尔可夫链预测模型应用在北江流域年降水量的预测，对年降水量状态做了预测分析，并依据遍历性有关理论对其重现期做了说明；但二者均只是根据降水量分级标准对预测年的降水量状态进行了预测分析，并没有对降水量的具体数值进行讨论计算。为此，选取铜川气象站1960—2013年的年降水量资料，采用样本均值-均方差分组法，建立符合铜川地区年降水量的分级标准以及状态分级[7-8]；并应用适用于当地的加权马尔可夫链模型对2014年和2015年的年降水量状态进行预测，为了确保预测结果的可靠性，同时采用模糊集理论中的级别特征值对2014年和2015年年降水量进行具体数值预测。
1960—2010年降水数据来自于中国国家级铜川站数据更正后的月报数据文件（A0/A1/A）基础资料集，结合陕西省历年统计年鉴可得2011—2013年降水数据。
1.2.1 马尔可夫链预测模型理论
马尔可夫过程是一种较普遍的随机过程，是指从一种状态转移到另一种状态随时间的变化所做的状态转移，即状态转移过程，一系列状态转移过程的总体称为马尔可夫链，其特点是无后效性[9]。无后效性是指一个时间序列中将来的状态与取值仅与现在的状态和取值有关，而与以前的状态与取值无关。
马尔可夫链是俄国学家Markov1906年提出的，是状态与时间参数都离散的过程，定义[10-11]为：设随机序{X(n)，n=1，2，…}的离散状态空间E，若对于任意m个非负整数n1，n2，…，nm(0≤n1＜n2＜…＜nm)和任意自然数k，以及任意i1，i2，…，im，j∈E，满足：
称{X(n),n=0，1，2，…}为马尔可夫链。在式（1）中，如果nm表示现在时刻，n1,n2,…，nm-1表示过去时刻，nm+k表示将来时刻，则此式表明在将来nm+k时刻处于状态j，仅依赖于现在nm时刻的im，而与过去m-1个时刻n1, n2,…，nm-1所处的状态无关。其中，式（1）等式右边条件概率形式为
，称为马尔可夫链在n时刻的k步转移概率，记为Pij(n,n+k)。他是不依赖于n的马尔可夫链，称为时齐马尔可夫链，仅与转移出发状态i、转移步数k、转移到达状态j有关，与起始时刻n无关。
1.2.2 加权马尔可夫链的预测步骤
①对历史数据进行分组；
②计算各阶的一步转移概率矩阵，P1，P2，…，Pk，I={1,2,…，K}，其中
,其他类推；
③“马氏性”检验[12-13]；设
为一步转移概率矩阵
表示指标序列
中从状态i经过一步转移到达状态j的频数，i,j∈E。将转移频数矩阵的第j列之和除以行各列的总和所得的值称为“边际概率”，记为p.j，则
（其中m表示研究序列所包含的状态）。统计量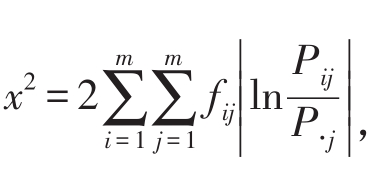
是以自由度为(m-1)2的x2分布，其中
给定显著性水平α，若x2＞x2α((m-1)2)，则认为{xi}符合马氏性，否则该序列不可作为马尔可夫链来处理。
④计算各阶相关系数[14-16]，即：
式中：rk为第k阶（滞时为k年）自相关系数；Xi为第i时段的指标值；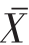
为指标均值；n为指标的序列长度。
对各阶自相关系数规范化，即:
式中：m为预测所需最大阶数。
⑤以前面序列若干时段（连续）为初始状态，结合相应的转移概率矩阵，即可预测得到该时段指标值的转移概率
，k为滞时（步长），k=1,2,…，m。
⑥预测n+1时段的状态：取状态空间E={1,2,…,5}，将同一状态的不同滞时的概率进行加权求和，就得到该状态下的预测概率，即：
该条件下对应的max{Pi}即可表示该时段指标值的预测状态。
⑦重复①—⑥，预测n+2时刻的状态，其余类推。
⑧进一步对该加权马尔可夫链的遍历性和平稳分布进行分析。
1.2.3 模糊集理论中的级别特征值
马尔可夫链模型采用概率最大隶属原则来确定预报对象的状态[17-18]，兹首先给各状态赋以相应的权重，由5个权重构成权重集：
其中权重取决于各状态概率的大小，即:
式中：η是最大概率的作用系数，其值通常取2或4，其值越大，越突出最大概率的作用，兹取4。级别特征值
如果根据最大概率确定的状态为i，且H＞i，则年降水量预报值为
；如果H＜i，则预报值为
其中Ti、Bi分别为状态区间值的上下限。
对于数据序列x1,x2,…,xn，可以看作是一个时间序列的前n个观测值，算出样本均值Xˉ和样本标准差s（基于给定的样本总体），采用样本均值-均方差分组法，将各年降水量确定为5个状态，如表1所示。据此可得研究区内1960—2013年年降水序列及其状态，如表2（其中Xˉ=589.41 mm，s=117.39 mm）。
表1 铜川地区年降水量分级标准
表2 铜川地区1960—2013年年降水量及对应状态
3.1.1 “马氏性”检验
据此，统计量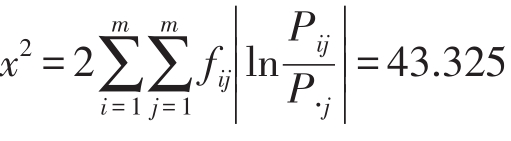
，给定显著性水平α=0.1时，查平方分布表可得
(16)=23.542，且
，即铜川地区降水量符合马氏性要求。
3.1.2 相关系数及权重的确定
根据式（2）求相关系数（此处取1～5阶、2～6阶自相关系数），再由式（3）求取对应的自相关系数的权重，如表3所示。
表3 1～5阶、2～6阶自相关系数和权重
兹采用1960—2010年年降水量数据求自相关系数和权重；而对应不同的预测年其自相关系数和权重是变化的；如当预测起始年为2007—2011年时，求其自相关系数和权重采用的数据便是1960—2011年年降水量数据。
3.1.3 模型检验及分析
基于2006—2010年的年降水量数据，采用1～5阶权重系数，对2011年年降水量进行预测，结果如表4所示。2011年的预测值为状态2，属于偏枯状态；根据模糊集理论，2011年的降水量预测值为502.48 mm，而2011年的降水量实测值为758.40 mm，相对误差接近50%，与预测状态相差较大。出现这种情况的原因可能是：①模型自身的缺陷；确定降水量状态分级标准时缺乏科学验证；同时，对某一年的降水量进行预测时，只是以被预测年份之前的5 a降水量数据作为基准对其进行分析，这将在一定程度上使预测结果更多地受所选预测起始年影响；②受大环境气候背景的影响；由《陕西省统计年鉴》可知，在关中地区2011年降水量整体异常偏多的背景下，使得铜川地区2011年降水量亦处于丰水年；如西安市2011年年降水量为723.6 mm，渭南市2011年年降水量为737.6 mm，咸阳市2011年年降水量为754.3 mm，宝鸡市2011年年降水量为1 025.6 mm，以上地区2011年均处于丰水年。基于上述分析，可以将2011年的年降水量数值作为异常值，且并不影响其他年份降水量预测。
基于2006—2010年的年降水量数据，采用2～6阶权重系数，对2012年年降水量进行预测，结果如表4所示。2012年的预测值为状态2，属于偏枯年；根据模糊集理论，同时求得预测值为473.53 mm，2012年的降水量的实测值为502.8 mm，相对误差为6.2%，与预测状态相吻合。
表4 2011年、2012年降水量预测
同理对2013年降水进行预测（预测起始年2008—2012年），采用1～5阶权重系数，结果如表5所示。2013年的预测值为状态2，实际2013年的降水量为516.20 mm，与预测状态相吻合。根据模糊集理论，同时求得预测值为529.67 mm，相对误差为2.5%。
表5 2013年降水量预测
将2011—2013年作为铜川地区降水量预测模型的验证期，其结果如表6所示。由表6可知，①同一预测起始年对相邻2 a的年降水量进行预测；预测起始年为2006—2010年时，分别对2011年和2012年降水量进行预测，其相对误差分别为50.9%和6.2%（由前述分析可得2011年为降水异常年）；同理预测起始年为2007—2011年时，对2012年和2013年降水量进行预测，其相对误差分别为2.6%和12.7%；预测起始年为2008—2012年时，对2012年和2013年降水量进行预测，其相对误差分别为2.5%和3.6%～9.8%；②不同预测起始年对相同年的年降水量进行预测；对2012年降水量预测，预测起始年为2007—2011年时，采用的是1～5阶预测，其相对误差为2.6%，而采用（预测起始年为2006—2010年）2～6阶进行预测时，其相对误差为6.2%；同理对2013年年降水量预测，采用（预测起始年为2008—2012年）1～5阶预测，其相对误差为2.5%，而采用（预测起始年为2007—2011年）2～6阶进行预测时，其相对误差为12.7%；由以上分析可得，除2011年为异常年外，无论对同一年还是相邻年的年降水量进行预测，采用1～5阶权重系数要比采用2～6阶权重系数对降水量预测的相对误差小，因此在已知当年降水量时要用1～5阶权重系数对降水量进行预测，有助于降低误差。同时，体现了该模型在铜川地区降水量预测的适用性很强，满足精度要求。
表6 不同预测起始年预测年降水量的相对误差
注 2014年相对误差根据预测状态对应的分级确定。
采用1～5阶和2～6阶自相关系数和权重分别对2014年和2015年降水量预测，预测结果如表7所示。由表7可知，2014年与2015年降水量的预测值均为状态3，属于正常年。再根据模糊集理论可得2014年与2015年的降水量预测值分别为585.82 mm和649.21 mm。
表7 2014年和2015年降水量预测
选取铜川地区1960—2013年的年降水量序列，以拟合性最好的二阶马尔可夫链为基础对其进行分析[19]。其中，枯水年、偏枯年、正常年、偏丰年和丰水年这5个状态是互通的，且都是非周期的，因此该马尔可夫链是一个不可约正常返链，由齐次马尔可夫链性质可知，该马尔可夫链具有遍历性，则说明经历一段时间，系统达到了平稳状态，此时的平稳分布即为其极限分布，且唯一[20]。
称概率分布{πj,j∈E} 为马尔可夫链的平稳分布，则满足：
据时间步长为2的转移概率矩阵可以求得极限分布πj和各状态出现的周期Tj，二者满足
，结果如表8所示。
表8 极限分布与状态周期
由表8可知，基于给定的分级标准，1960—2013年的降水过程，偏枯年份出现的概率最大为0.335，平均每隔2.983 a出现1次；枯水年份出现的概率最小为0.089，平均每隔11.247 a出现1次；对于正常年而言，其出现的概率（0.257）仅次于概率最大的偏枯年，平均3.891 a出现1次。
1）依据铜川1960—2013年现有的年降水量资料，采用样本均值-均方差分组方法，建立了降水量分级标准（分级系数分别为0.35和1.1），确定了枯水年、偏枯年、正常年、偏丰年和丰水年5个状态；采用统计的方法验证了该降水时间序列符合马尔可夫性，建立了相关的加权马尔可夫链预测模型；利用马尔可夫链的遍历性，得出铜川处于偏枯年的概率较大，枯水年和丰水年出现的概率较小，正常年出现概率仅次于偏枯年。
2）通过对2011、2012和2013年的年降水量预测可以发现，采用1～5阶预测要比采用2～6阶预测的相对误差小。因此，在资料允许的情况下，要尽量采用1～5阶进行预测，避免出现误差较大的情况。
3）采用已建立的马尔可夫链预测模型，根据已有数据对模型的可靠性进行了验证，结果表明预测结果符合实际，满足预测的精度要求，说明该模型具有预测该地区年降水量的能力；因此，在现有的降水量资料的基础上，采用1～5阶及2～6阶的自相关系数对2014和2015年的降水状态进行了预测，即2014、2015年均为正常年；根据模糊集理论中的特征值求得2014年的降水量为585.82 mm，2015年的降水量为649.21 mm。
4）2011年年降水量的预测值与实际值偏差很大，超出精度要求，其原因可能是模型自身的缺陷，确定降水量状态分级标准时缺乏科学验证，预测起始年不同对预测结果产生一定影响；受大环境气候背景的影响，导致2011年降水量出现较大的变化；因此可将2011年作为异常年份，并不影响后续年份的降水量预测。
对降水量进行预测时，跟初始的数据量有很大的关系，如不能提供足够长的降水量序列，势必会影响降雨量的预测；状态分级时，没有一个特定的标准，只是基本满足该地区的降雨量特征，其状态结果也是一个易受主观影响的数值。因此，对于这方面的应用还需要进一步深入研究。
参考文献：
[1]赵欣，邹良超，倪林．基于有序聚类的模糊加权马尔可夫模型在降雨预测中的应用[J].江西农业学报，2009,21（2）：110-113．
[2]李娟，张维江，马铁．滑动平均—马尔可夫模型在降水预测中的应用[J].水土保持研究，2005,12（6）：196-198．
[3]白玉洁．改进时间序列模型在降雨量预测中的应用研究[J].计算机仿真，2011,28（10）：141-145．
[4]刘德地，陈晓红．一种北江流域年降雨量的权马尔可夫链预测模型[J].水文，2006,26(6)：23-26．
[5]孙才志，张戈，林学钰．加权马尔可夫链在降水丰枯状况预测中的应用[J].系统工程理论与实践，2003(4)：100-105．
[6]王艳，毛明志，范晶，等．最优分割法确定的加权马尔可夫链在降雨量预测中的应用[J].统计与决策，2009（11）：17-18．
[7]夏乐天，朱元甡，沈永梅．加权马尔可夫链在降水状况预测中的应用[J].水利水电科技进展，2006,26（6）：20-23．
[8]潘刚，芦冰，邹兵，等．马尔可夫链在水库主汛期降雨状态预测中的应用[J].水利科技与经济，2011,17（6）：33-36．
[9]赵建辉．降雨量预测的马尔可夫链模型[J].河北水利，1994（2）：28-29．
[10]刘建民.随机过程[M].西安：西北大学出版社，2004：66-67．
[11]夏乐天.马尔可夫链预测方法及其在水文序列中的应用研究[D].南京：河海大学，2005．
[12]张玉芬，朱雅琳．马尔可夫链极其检验方法研究[J].价值工程，2012（2），312-313．
[13]王佐仁．马氏链为齐次的统计检验方法[J].统计与信息论坛，2004，19（3），14-15．
[14]王涛，钱会，李培月．加权马尔可夫链在银川地区降雨量预测中的应用[J].南水北调与水利科技，2010,8（1）：78-81．
[15]仲远见，李靖，王龙．改进马尔可夫链降雨量预测模型的应用[J].济南大学学报，2009，23（4）：402-405．
[16]周庆欣，吴玉东，范红霞，等．加权Markov链权重计算及其应用[J].哈尔滨商业大学学报（自然科学版），2014,30（6）：740-743．
[17]孙才志，林学钰．降水预测的模糊权马尔可夫模型及应用[J].系统工程学报，2003,18（4）：294-299．
[18]岳瑶，李天宏．基于模糊集理论的马尔可夫模型在水质定量预测中的应用[J].应用基础与工程科学学报，2011,19（2）：231-242．
[19]张宗国．马尔可夫链预测方法及其应用研究[D].南京：河海大学，2005．
[20]刘秀芹，赵玉玲，范玉姝．剖析马氏链平稳分布的讲解——谈《应用随机过程》教学[J].大学数学，2011,27（4）：199-202．
Predicting Precipitation in Tongchuan Using Weighting Markov Chain Model
LI Yabin1,2，XU Panpan1,2，QIAN hui1,2，WANG Haike1,2
（1.School of Environment Science and Engineering,Chang’an University,Xi’an 710054,China；2.Key Laboratory of Subsurface Hydrology and Ecological Effects in Arid Region,Ministry of Education,Chang’an University,Xi’an 710054,China）
Abstract:This paper analyzed the statistics of temporal variation of precipitation in Tongchuan of Shanxi Province using rainfall data measured from 1960—2013 and the sample-mean method and the square-moment method.We first demonstrated that the temporal series of the precipitation is statistically Markovian,and then developed a weighting Markov Chain model to predict the precipitation and tested it against available data in this region.The model was further combined with the fuzzy theory to predict rainfall.The results showed that the model is accurate and reduces error when using 1-5 backward precipitations.The model predicted that both 2014 and 2015 were weakly drought with an annual rainfall of 585.82 mm and 649.21 mm respectively,and that the possibility of occurrence of normaland weak drought yearswere high,while the occurrence of drought year was statistically low.
Key words:weighted Markov chain;Tongchuan area;prediction of precipitation;fuzzy set theory;ergodic and stationary distribution
中图分类号：P468.0+24
文献标志码：A
doi：10.13522/j.cnki.ggps.2017.05.017
责任编辑：刘春成
李亚斌，徐盼盼，钱会，等．加权马尔可夫链在铜川地区降水量预测中的应用[J]．灌溉排水学报，2017，36（5）：96-102.
收稿日期：2016-10-03
项目基金：水利部公益性行业科研专项经费项目（201301084）
作者简介：李亚斌（1990-），男，山西晋城人。硕士研究生，主要从事水文地质方面的研究。E-mail:m15702928017_1@163.com
通信作者：钱会（1963-），男，陕西咸阳人。教授，博士生导师，博士，主要从事水文地质方面的研究。E-mail：55480981@qq.com
文章编号：1672-3317（2017）05-0096-07