沈 婧,樊贵盛
(太原理工大学 水利科学与工程学院,太原 030024)
摘 要:为满足季节性冻土地区越冬期间储水灌溉管理的需求,基于山西省汾河灌区季节性冻土的冬季大田土壤水分入渗试验,得到了120组Philip入渗模型参数实测样本,借助MATLAB软件,建立了以土壤温度、有机质质量分数、土壤含水率、土壤体积质量、物理性黏粒量为输入因子、以Philip入渗模型参数吸渗率和稳渗率为输出因子的多元非线性传输函数模型,并用实测资料对该模型进行了精度检验。结果表明,预测参数的相对误差均小于11%,预报精度在可接受范围之内。
关键词:冻融土壤;土壤理化参数;土壤传输函数;Philip入渗模型参数;非线性预测
季节性冻土[1]是一种含有冰晶体的特殊土水体系,集中分布在华北和西北地区,其面积约占我国国土面积的一半,是我国耕作土地资源的主要组成部分。随着水资源供需矛盾的加剧,农业用水被挤占问题越来越凸显,因而在农闲季节,也就是北方地区的冬季,冬季耕作土地土壤储水灌溉已成为一种客观需求。因此,越冬期灌溉用水管理的技术问题越来越被重视。影响越冬期的农田灌溉质量的首要技术参数——土壤水分入渗参数便成为专家学者关注的重点。国内外众多学者对冻融土壤水分入渗问题展开了研究,何志萍等[2]历时2个冬春进行了228组试验,研究冻融土壤水分入渗的特性;李天霄[3]得出:冻融土壤条件下水分入渗过程达到相对稳定的时间与非冻融土壤条件下所需的时间存在明显差异,并且冻深对入渗能力的影响在不同时期是不同的;Weigert等[4]研究了冬季期间水分在土壤中的运移情况;Lilbaek等[5]模拟了积雪融化水进入冻融土壤的入渗过程。
有关季节性冻土区冻融土壤入渗特性的研究正在向纵深发展,但由于客观条件和试验设备的限制,人们直接测定土壤入渗参数既费力又耗时,尤其是越冬期间土壤入渗参数的测定更困难,于是引入了土壤传输函数理论[6],即建立土壤理化参数与入渗参数之间的函数关系,用较易获得的理化参数预测不易获得的入渗参数。近些年,土壤传递函数频频出现在研究土壤水分运动参数和入渗参数的文献里,如:Sobieraj等[7]借助土壤传输函数预测土壤水力传导度;贾宏伟等[8]通过建立土壤转换函数,用土壤含水率、沙粒量和粗粉粒量估算简化了的Philip入渗模型中的入渗参数;刘继龙[9]用基于耕作层和犁底层的土壤理化参数所建立的土壤传递函数去估算土壤水分运动参数,为构建估算较大区域尺度上水分运动参数的土壤传递函数提供了借鉴和参考;费良军等[10]建立了用土壤物理参数估算标定因子的土壤转换函数,为解决区域尺度内土壤入渗参数的点面转换问题提供了方法;郭中领[11]借助土壤传输函数预测北京地区饱和土壤导水率;冯锦萍、刘珊珊等[12-13]分别基于Kostiakov三参数入渗模型、Green-Ampt入渗模型建立土壤传输函数,对非冻融土壤的入渗参数进行了预测。综上所述,人们对预测土壤水分入渗参数的研究已较多,但基于Philip[14]半经验半理论入渗模型,对冻融土壤水分入渗参数的预测研究鲜见报道。
基于季节性冻土的大田土壤入渗试验样本,利用土壤传输函数的方法,建立冻融土壤Philip入渗模型参数的非线性传输函数模型,实现了以土壤常规理化参数为输入因子对入渗参数进行预测,一方面为季节性冻土的冬春灌溉灌水技术参数的预测提供了技术手段,另一方面在广度上促进了土壤传输函数理论的发展。
大田入渗试验地点在山西省平遥县(宁固镇和北长寿村)和山西省中心灌溉试验站(文水县刘胡兰镇)进行,均位于山西省汾河灌区内。试验区属于大陆性半干旱季风气候,年内温差较大,降雨量分配极不均匀,7、8、9月温度较高,最高可达40◦C左右,全年主要降雨量也集中在这3个月。霜冻期始于11月下旬终于次年3月下旬,试验期间土壤温度最低-9.5◦C,最高16.5◦C,冰冻层厚度为0~65cm不等。
试验区属冲积平原地貌,地形平缓,土壤母质为河流冲、洪沉积物,土壤类型为浅色草甸土,地下水埋深在1.0~3.5m之间,土壤有机质(0~20cm)质量分数介于0.49~1.41g/kg之间;土壤体积含水率范围是4.03%~47.06%(0~20cm)和5.29%~49.22%(20~40cm);土壤体积质量在0.89~1.81g/cm(30~20cm)和0.84~1.59g/cm(320~40cm)之间;物理性黏粒量为7.60%~48.98%(0~20cm)和6.01%~39.20%(20~40cm)。
试验开始于2014年10月下旬,次年4月上旬结束。为避免土壤冻结后入渗环不易埋设,在10月初将上百套双套环入渗仪(内、外环直径分别为26cm、60cm,高度均为25cm)预埋设至地表以下20cm的深度。双套环为2个同心圆环,内环控制试验入渗面积,外环起保证内环水体垂直下渗、尽量减少侧向渗流的作用。用自制的水位控制器对内、外环水位进行控制,均保持在地表以上2cm处。试验过程中,准确记录内环加水的时间和水量,但无需测定外环加水时间及水量。试验研究表明,土壤水分入渗在60min左右基本达到稳定入渗,本试验选定入渗时间为90min,以确保大田土壤水分入渗都达到稳定入渗状态。
本建模样本涉及到的土壤理化参数有土壤温度、土壤有机质、土壤质地、土壤体积含水率和土壤体积质量。土壤温度的测定采用预埋的热敏电阻获得;有机质质量分数是利用化学方法通过重铬酸钾容量法来测定;土壤质地通过筛分+比重计法得到筛分曲线,然后分析土壤的颗粒级配,进而确定土壤质地;土壤体积含水率用传统烘干称质量法测量获得;土壤体积质量通过蜡封法进行测定得到;气温等其他信息采用试验站气象设施观察得到。
1957年,在系统研究Richard方程的基础上,Philip[14]提出了能较好地描述土壤水分一维垂直入渗情况的入渗模型,该模型是半经验半理论性的模型,具有明确的物理意义,入渗公式中只含有2个入渗参数,形式简单,因而得到广泛应用[15]。Philip入渗公式为:
式中:I为累积入渗量:自入渗开始至t时刻的入渗总量(cm);S为吸渗率:入渗开始后第一个单位时段末的累积入渗量与稳定入渗率之差,在数值上等于入渗开始至1min末的累积入渗量减去稳渗率(cm/min0.5);t为入渗历时(min);A为稳渗率,在单位势梯度下饱和土壤的入渗速度或非饱和土壤入渗达到相对稳定阶段的入渗速度(cm/min)[16]。
建模样本根据实测的大田冻融土壤的系列入渗试验数据建立。试验可得到累积入渗量I90和入渗历时t与阶段入渗量I'的关系,由实测的t-I'点群关系拟合出Philip入渗公式中的S和A。同时,试验过程中同步测定出对应的土壤常规理化参数。由Philip入渗模型参数和土壤常规理化参数共同构成建模样本,表1给出20组样本数据。
兹建立了由120组Philip入渗模型参数和冻融土壤常规理化参数构成的样本,其中112组作为建模训练样本,8组作为所建预测模型的检验样本。
表1 样本数据
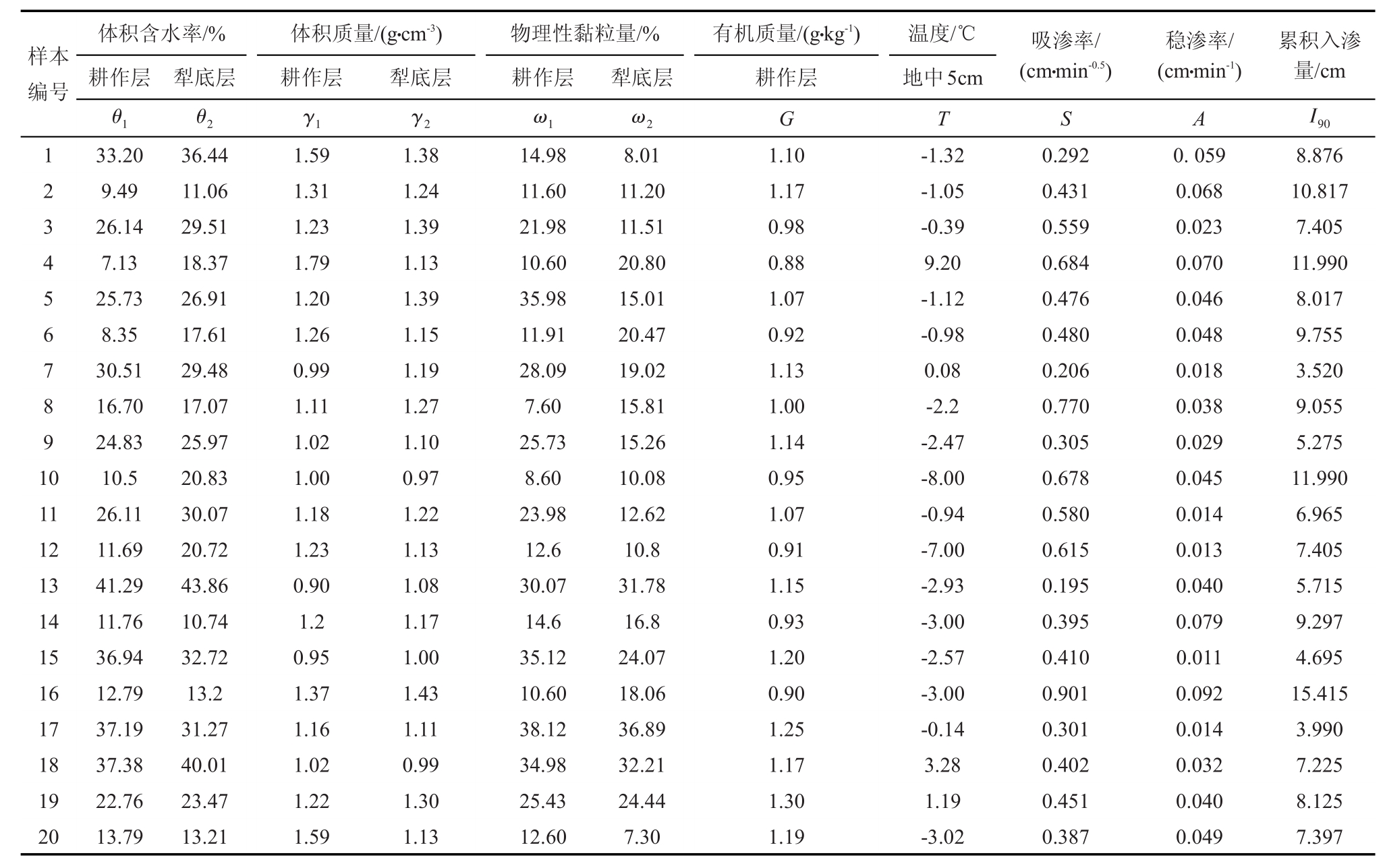
注 表中耕作层即前文所写的0~20cm土层,犁底层即20~40cm土层,土壤温度取地表以下5cm处土壤温度。
1)土壤温度:地温越低,土壤中相变成冰的液态水越多,冰晶体积膨胀,占据了导水孔隙的一部分,使孔隙孔径减小,S和A减小。
2)土壤有机质:土壤通透性、孔隙大小分配的合理性及孔隙稳定性均与有机质量有关。有机质量低的土壤,较大、较小孔隙居多,水分进入土壤初期,较大孔隙先充满水,并在重力作用下向下层土壤入渗,S较大;反之,有机质量高的土壤,中等孔隙发育较好,在水分入渗初期,S较小。稳渗率A的大小主要由孔隙的大小和多少决定,有机质量低的土壤,大孔隙和小孔隙居多且土壤团粒结构稳定性差,入渗过程中,土粒容易随着水流移动,使小孔隙孔径减小,甚者堵塞小孔隙,迫使入渗水流改变方向,下渗路径曲折蜿蜒,A较小;而有机质量高的土壤,中等孔隙居多且土壤团粒结构稳定性较好,A较大。
3)土壤结构:土壤结构是指耕层土壤的松紧程度、孔隙程度和板结程度,常用土壤体积质量表征。体积质量越大,土壤越密实,土壤孔隙就小,孔隙连通性差,水分入渗路径越弯曲,水流受到的阻力越大,单位势梯度下,水分通量小,土壤的水力传导度就小,则S和A越小;反之,S和A越大。
4)土壤质地:土壤质地的分类和划分标准有很多种,兹采用卡庆斯基制对土壤质地进行划分,并以物理性黏粒量(<0.01mm)作为数学表征值。土壤物理性黏粒量越多,固体相比表面积越大,颗粒表面的吸附能力越大,粒间孔隙越小,加之部分土壤液态水相变成冰后,冰晶体积膨胀使较大孔隙孔径变小、较小孔隙孔径更小,甚至堵塞孔隙,入渗水流路径严重曲折,导致水分通量较小,水力传导度低,S和A都减小。
5)土壤含水率:土壤含水率决定着土壤固、液相的比例,常用体积含水率表示。在入渗开始后的很短时间内,表层土壤很快达到饱和,若含水率大,势梯度就小,单位过水断面的入渗通量就小,S、A就越小。
6)冰冻层:冰冻层形成的物质基础是土壤液态水、客观条件是土壤温度,液态水越多、土壤温度越低,冰冻量越大。冰冻层的形态、层数、厚度和层位对冻融土壤水分入渗过程的影响是间接的,土壤液态水相变成冰后、冰晶体积膨胀、孔隙减少、导水率降低,导致土壤入渗能力降低[17]。
7)气温和水温:气温和水温对入渗能力的影响都是通过土壤温度实现的。气温和水温越高,土壤温度越高。
8)地下水埋深:地下水对入渗的影响是通过地表含水率来实现的,地下水埋深越浅,入渗能力越小[18]。
9)其他因素:土壤水分入渗是个非常复杂的过程,影响入渗能力的因素有很多,与以上列举的影响因素相比,其他因素对入渗能力的影响并不显著,同时考虑到入渗模型的简便性,故将其他因素对入渗参数的影响简化为常数关系。
输出因子为Philip入渗模型的入渗参数:吸渗率S和稳渗率A。
输入因子根据2.1分析的主要因素初步确定,然后由输入变量的显著性检验决定取舍。在输入因子的初步确定的同时,应考虑以下3点:
1)华氏温度(F)的引入。考虑到模型检验中对变量非零和非负的要求,可以把土壤温度的单位由摄氏度换算成华氏度,换算公式:F=1.8T+32,当华氏温度为0℉时,此时对应的摄氏温度为-17.78℃,该温度能满足本次试验土壤温度的下限,故将摄氏度换算成华氏度后,能保证土温的非负性和非零性。
2)间接影响因素的舍弃。冰冻层、气温和水温、地下水埋深通过地温、含水率对土壤水分入渗能力产生影响,故不作为输入因子。
3)入渗参数受土壤层次的影响。从吸渗率S的概念可知,入渗开始较短时间内,水分还未能到达犁底层,故影响S的因素仅限于耕作层;而影响A的因素既有耕作层也有犁底层。
那么,初步确定吸渗率S的输入因子为:地中5cm深处的华氏温度T、有机质质量分数G、物理性黏粒量ω1、土壤体积质量γ1、土壤体积含水率θ1;初步确定A的输入因子为:地中5cm深处的华氏温度F、有机质质量分数G、耕作层和犁底层的物理性黏粒量ω1和ω2、耕作层和犁底层的土壤体积质量γ1和γ2、耕作层和犁底层的土壤体积含水率θ1和θ2。
建立模型的目的是找到一个数学表达式,以测定的土壤常规理化参数为输入因子,计算出不易测定的入渗参数。基于冻融土壤田间入渗试验样本,借助MATLAB[19]软件,建立冻融条件下Philip入渗模型参数与其土壤理化参数间的关系模型。其具体操作步骤和结果为:
1)确定入渗参数与单个输入因子的函数关系。运用控制变量法,选择一个因子作为唯一变量,要求其他因子相同或相近,对数据进行筛选,选出5~10组满足要求的数据,借助MATLAB软件的Cftool功能[19],输入单个因子及入渗参数的实测值,由离散点的走势,选择或定义函数形式,参考拟合效果,最终确定函数的最佳形式。
经拟合后,入渗参数与各输入因子的函数关系最终确定为:地温与入渗参数呈线性关系;土壤含水率与入渗参数的关系既包含对数关系又包含线性关系;土壤体积质量与入渗参数的关系既包含对数关系又包含线性关系;土壤有机质质量分数与入渗参数呈对数关系;土壤物理性黏粒量与吸渗率S的关系既包含对数关系又包含线性关系,而与稳渗率A只呈对数关系。
2)确定回归方程的初步形式。将拟合出的函数关系进行机械相加,并添加一个常数项φ,便得出回归方程的初步形式:
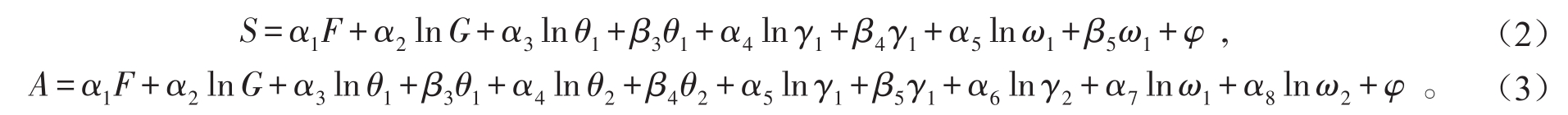
3)回归方程中自变量的显著性检验(T检验)。将样本数据和模型的初步函数形式输入到已编好的程序中,运行后可得到初步模型各项输入变量前的回归系数及其进行t检验后的结果,若存在某个|t|≤t0.05/2的值(显著水平α=0.05,t0.05/2=2.0141),则剔除掉最小t值所对应的自变量,继续对剩余自变量进行t检验,直至所有自变量对应的|t|值都大于t0.05/2后,停止检验。表2为所有自变量进行t检验的过程和结果。
由表2可知,吸渗率S经过2次检验、稳渗率A经过4次检验以后,剩余自变量的|t|都大于t0.05/2,那么通过t检验的自变量在入渗参数的回归方程中显著。
4)回归方程的显著检验(F检验)。除了要对方程自变量进行显著性检验,还要对整个回归方程自身进行显著性检验,即F检验,以确保回归方程显著。给定显著水平α=0.05,由样本情况查表可知Fα=0.05值,若计算得到的F大于Fα=0.05,则方程显著;反之,不显著。F检验结果见表3。
表2 t检验过程及结果
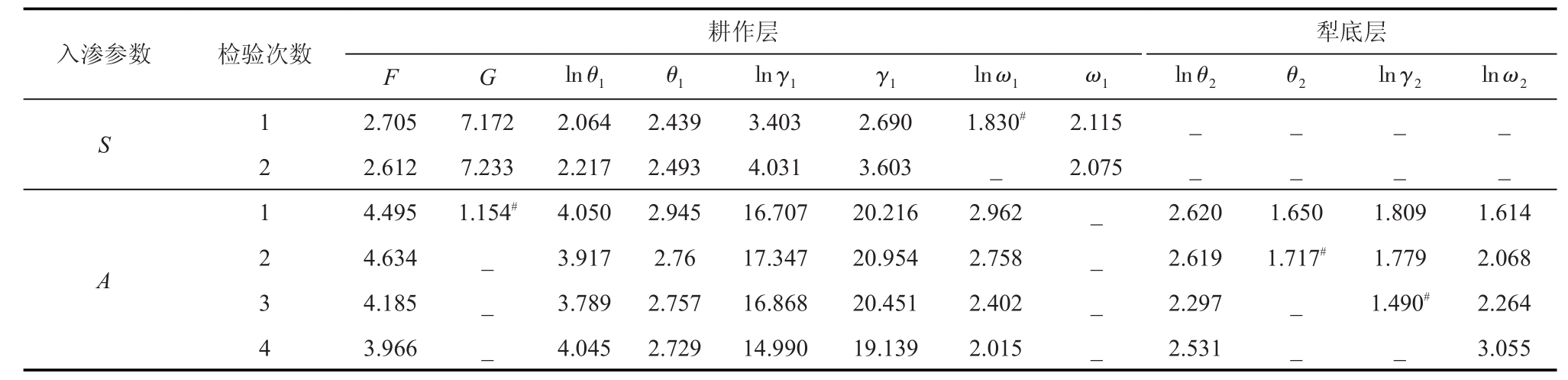
注 t0.05/2=2.014 41,每次检验结果中的最小值用#标注。
由表3可知,FS和FA都大于Fα=0.05,即入渗参数S和A的回归方程显著,二者的平均误差分别为9.964%、10.255%。则入渗参数的回归方程的最终形式为:
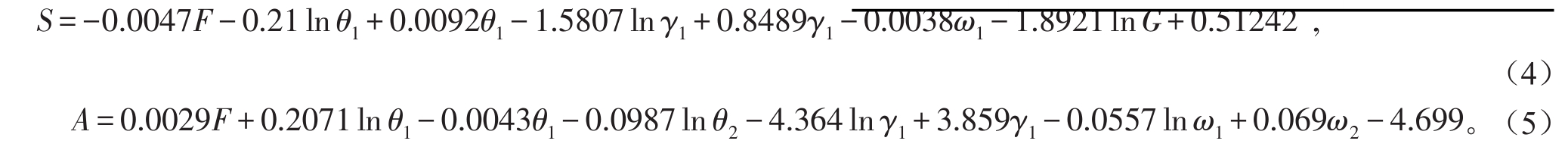
表3 F检验结果
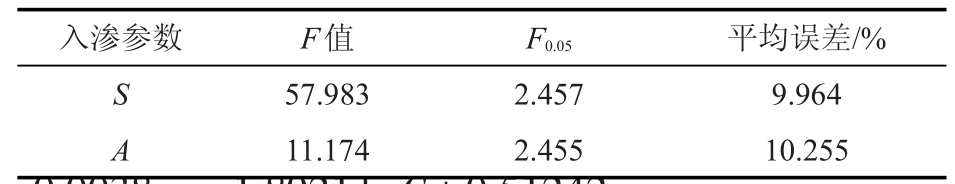
表4是预留8组检验样本的土壤条件,采用所建模型对检验样本的入渗参数进行预报,预报结果见表5。
表4 检验样本的土壤条件
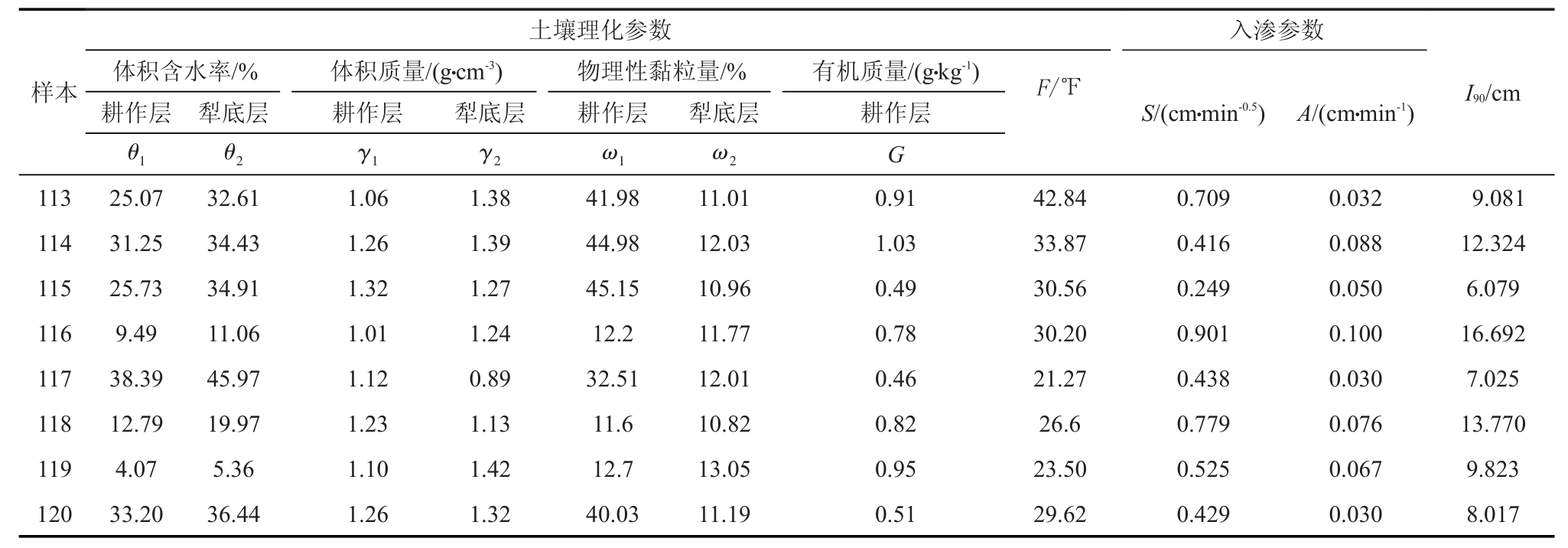
表5 预报结果

由表5可知,预测吸渗率S的相对误差范围为2.116%~7.547%,平均相对误差为4.512%;预测稳渗率A的相对误差范围为3%~13.333%,平均相对误差为8.368%,预测结果的精度在可接受范围之内。
将120组样本数据预测的A和S,带入Phillip入渗公式中,得到累积入渗量I90的计算值。将一一对应的实测I90与计算I90绘于1∶1直线图中,见图1。
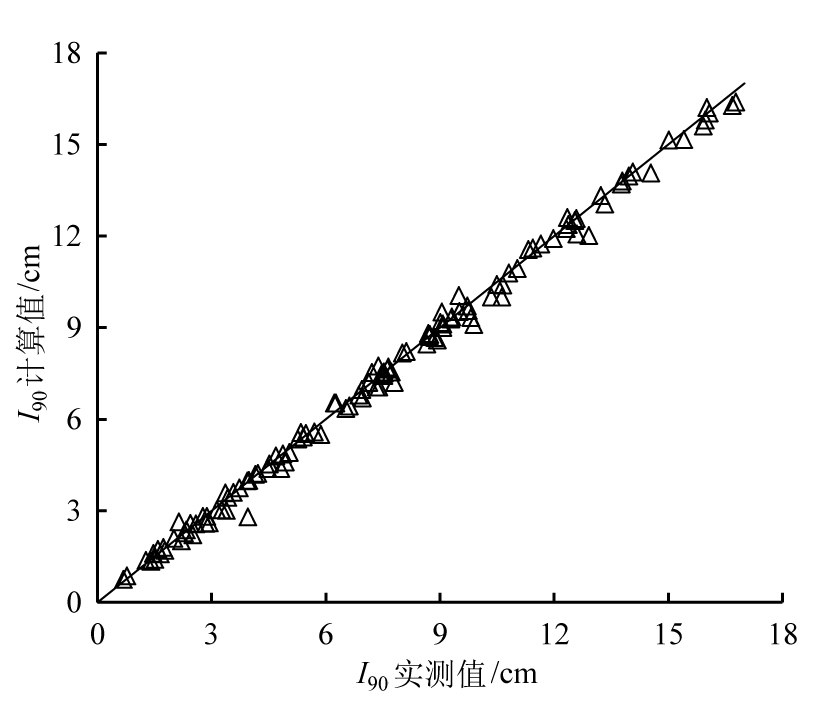
图1 I90计算值与实测值的比较
由图1可知,数据点大部分落在1∶1直线上,说明I90实测值与I90计算值比较接近,误差较小,进一步说明所建模型的预报精度较高。
目前,土壤水分入渗参数的预报模型主要有线性模型、非线性模型、BP神经网络模型,大量试验研究表明[12,15-16,18],预报精度由高到低排列为BP神经网络模型>非线性模型>线性模型,用线性关系描述土壤理化特性与入渗参数之间的复杂非线性关系显然很牵强,BP神经网络具有极强的非线性逼近能力,但为寻求最佳预报效果,需要花大量的时间进行反复迭代试算,相比较而言,非线性预报模型更准确、简便。
基于季节性冻土区冬季大田土壤水分入渗样本所建立的Philip入渗模型参数吸渗率和稳渗率的多元非线性传输函数模型。以土壤常规理化参数为输入因子,对冻融土壤Philip入渗模型参数A和S进行预报,2个入渗参数的平均预测误差都小于11%,误差在建模误差范围之内,故所建模型是可行的。用实测样本对预报模型进行单参数、二参数综合检验,检验精度亦在可接受范围。故该模型可作为预测冻融土壤入渗参数的方法。
由于越冬期冻融土壤试验的难度较大,试验数据精度的控制也较困难,因此本文建模所基于的样本数量有限,所建模型的精度有提高的空间,后续的研究中一方面应增加样本长度,另一方面可在样本代表性方面进行改进,以建立精度更高的多元非线性传输函数模型。
参考文献:
[1]樊贵盛,李雪转,李红星.非饱和土壤介质水分入渗问题的试验研究[M].北京:中国水利水电出版社,2012.
[2]何志萍,周瑞清.冻融条件下田间入渗特性分析[J].山西水利科技,2002(2):94-96.
[3]李天霄.北方季节性冻土区农田土壤水分运动规律研究[D].哈尔滨:东北农业大学,2010.
[4]WEIGERTA,SCHMIDT J.Water transport under winter conditions[J].CATENA,2005,64(2/3):193-208.
[5]LILBAEK G,POMEROY J W.Modelling enhanced infiltration of snowmelt ions into frozen soil[J].Hydrological Processes,2007,21(19):2 641-2 649.
[6]朱安宁,张佳宝,陈效民,等.封丘地区土壤传输函数的研究[J].土壤学报,2003,40(1):54-59.
[7]SOBIERAJ J A,ELSENBEER H,VERTESSY R A.Pedotransfer function for estimating saturated hydraulic conductivity:Implications for Modeling Storm Flow Generation[J].Journal of Hydrology,2001,251:202-220.
[8]贾宏伟,康绍忠,张富仓,等.石羊河流域平原区土壤入渗特性空间变异的研究[J].水科学进展,2006,17(4):471-476.
[9]刘继龙.土壤水分特性的分形特征与传递函数研究[D].杨凌:西北农林科技大学,2010.
[10]聂卫波,费良军,马孝义.区域尺度土壤入渗参数空间变异性规律研究[J].农业机械学报,2011,42(7):102-108.
[11]郭中领.北京地区土壤入渗研究[D].北京:北京师范大学,2009.
[12]冯锦萍,樊贵盛.土壤入渗参数的线性传输函数研究[J].中国农村水利水电,2014(9):8-11.
[13]刘姗姗,白美健,许迪,等.Green-Ampt模型参数简化及与土壤物理参数的关系[J].农业工程学报,2012,28(1):106-110.
[14]PHILIP J R.The theory of infiltration about sorptivity and algebraic infiltration equations[J].Soil Science,1957,84(4):257-264.
[15]原林虎.PHILIP入渗模型参数预报模型研究与应用[D].太原:太原理工大学,2013.
[16]岳海晶,樊贵盛.备耕头水地土壤入渗参数的线性预报模型[J].中国农村水利水电,2016(2):21-26.
[17]樊贵盛,郑秀清,贾宏骥.季节性冻融土壤的冻融特点和减渗特性的研究[J].土壤学报,2000,37(1):24-32.
[18]樊贵盛,郑秀清,潘光在.地下水埋深对冻融土壤水分入渗特性影响的试验研究[J].水利学报,1999,30(3):21-26.
[19]汪岚,黄彩虹.基于MATLAB色差预测多元回归模型的研究[J].计算机与应用化学,2008,25(8):1 015-1 018.
Estimating Philip Infiltration Parameter Using Nonlinear Transfer Function for Water Infiltration in Seasonal Frozen Soil
SHEN Jing,FAN Guisheng
(College of Hydro Science and Engineering of Taiyuan University Technology,Taiyuan 030024,China)
Abstract:This paper investigated the demand for water storage forirrigation in winter.We took Linfen Irrigation District in Shanxin Province as an example and measured water infiltrations in frozen soil.We first fitted the infiltration results to the Phillip infiltration formula and obtained 120sets of parameters,and we then linked the parameters to other easy-to-measure soil properties including soil temperature,soil organic matter,soil moisture content,soil bulk density and clay content using the multivariate nonlinear transfer function.The transfer function model could predict infiltration rate and steady infiltration rate in the Philip infiltration formula.The accuracy of the model was tested against measurements.The results showed that the errors of all predicted parameters were less than 11%.
Key words:thawing soil;soil physicochemical parameters;soil transfer function;Philip infiltration model parameters;multivariate nonlinear prediction
中图分类号:S152.7;TV93
文献标志码:A
doi:10.13522/j.cnki.ggps.2017.06.009
责任编辑:陆红飞
沈婧,樊贵盛.冻融土壤Philip入渗模型参数的非线性传输函数模型研究[J].灌溉排水学报,2017,36(6):42-48.
文章编号:1672–3317(2017)06-0042-07
收稿日期:2016-10-17
基金项目:国家自然科学基金项目(40671081);山西省水利厅科研项目—山西省地面畦灌节水技术参数手册研编
作者简介:沈婧(1990-),女,内蒙古赤峰人。硕士研究生,主要从事节水理论与技术研究。E-mail:1515064412@qq.com
通信作者:樊贵盛(1955-),男,山西孝义人。教授,博士生导师,主要从事土壤物理、灌排理论与技术研究。E-mail:fanguis5507@263.net