渠道保温防冻胀中冻土层等效导热系数的计算

张宇峰1，何武全2，赵彦琳1

（1.杨凌职业技术学院，陕西杨凌 712100；2.西北农林科技大学水利与建筑工程学院，陕西杨凌712100）

摘 要：针对渠道保温防冻胀设计中计算保温板厚度时关键参数冻土层等效导热系数采用经验法确定、计算误差大等问题，建立了北方寒冷地区粉质黏土的基于分形理论的冻土层等效导热系数λ*的计算公式，利用蛤蟆通灌区试验资料拟合得到系数C的计算公式，并通过内蒙古河套灌区、新疆冲乎尔灌区和黑龙江蛤蟆通灌区渠道保温防冻胀试验资料对建立的冻土层等效导热系数公式进行了验证。结果表明，计算得到的聚苯板厚度与试验观测的最佳厚度基本一致，最大相对误差仅为7.0%，说明其计算精度较高。利用该公式计算得出了粉土及粉质黏土常用冻土层等效导热系数，对于地下水埋深较浅、渠基土冻结期间存在水分迁移、冻胀较为严重的地区，在实际工程应用中可根据设计渠道情况进行选用。

关键词：渠道防渗；保温防冻胀；分形理论；等效导热系数

0 引言

我国季节性冻土地区面积占全国面积53.5%，季节性冻土区面积超过国土面积的1/2[1]。渠道冻胀破坏是我国北方季节性冻土地区发展渠道衬砌与防渗工程技术的关键制约因素。渠道保温防冻胀工程应用中，冻土层等效导热系数是渠道保温防冻胀设计中保温层厚度计算的重要参数，但是目前多采用经验公式确定，计算误差较大。在冻土层等效导热系数研究方面，根据试验资料建立了强冻胀土地区的冻土层等效导热系数计算经验公式，但没有考虑土层含水率和土壤水分迁移的影响[2-3]；提出了基于部分保温法的渠道保温板厚度计算方法，并结合工程实际资料通过数值模拟对其计算方法进行了验证，但冻土层等效导热系数取值偏大[4]；基于热传导原理和热阻等效原理，拟合了冻土层等效导热系数和地下水位的计算关系，但忽略了含水率和土壤结构的影响[5-6]；分析了渠道不同坡面、部位和板厚在多个埋深处的地温、冻深、含水率和冻胀量变化规律及其特征，总结了铺设聚苯乙烯保温板的厚度，但此计算厚度的经济合理性有待提高[7]。近年来，国内外专家学者开始将分形理论引入到土壤导热系数计算中，根据分形理论对多孔介质的几何结构进行了描述，建立了土壤结构分形模型，为土壤导热系数的计算提供了新思路[8-9]。但是，针对渠道保温防冻胀中冻土层等效导热系数计算时考虑因素不全面，计算误差较大。为此，将分形理论引入到冻土层等效导热系数的计算中，建立基于分形理论的渠道保温防冻胀冻土层等效导热系数λ*的计算公式，为季节性冻土地区渠道防渗保温防冻胀技术的进一步推广应用提供一定参考。

1 渠道防渗保温防冻胀应用情况

在渠道防渗保温防冻胀技术应用方面，通过对我国西北、东北、华北等北方季节性冻土地区渠道保温防冻胀技术应用情况的调查分析表明，聚苯板保温防冻胀技术已开始广泛应用于渠道衬砌防渗工程中，并且防冻胀破坏的效果较为理想。内蒙古、甘肃、宁夏、河北、辽宁和吉林等省（区），近年来结合全国大型灌区续建配套与节水改造项目，均开展了渠道保温防冻胀技术的试验与示范应用，其中采用聚苯板保温防冻胀已经在内蒙古河套灌区和宁夏引黄灌区的骨干渠道上大面积推广应用。目前渠道保温防冻胀主要分为“现浇混凝土板+复合土工膜+保温板”和“预制混凝土板+砂浆过渡层+防渗膜料+保温板”2种结构[10]，保温板厚度计算采用基于热阻等效原理的计算公式，即：

式中：S为保温层厚度（m）；λs为保温层导热系数（W/（m·K））；Z为天然冻土层厚度（m）；Z1为预留冻土层厚度（m）；λ*为冻土层等效导热系数（W/（m·K））；Sh为混凝土衬砌板的厚度（m）；λh为混凝土导热系数（W/（m·K））；Sf为防渗膜料层的厚度（m）；λf为防渗膜料层的热阻（W/（m·K））。

由式（1）可以看出，在渠道基土参数及防渗保温材料确定时，只要知道冻土层等效导热系数，就可以计算保温板的厚度。

2 冻土层等效导热系数计算方法

渠道防渗保温防冻胀工程设计中，在计算保温板厚度时，冻土层等效导热系数是一个关键参数，以往计算冻土层等效导热系数均是采用特定条件下的经验公式，计算误差较大，不能满足实际工程应用的要求。根据以往研究，冻土层等效导热系数与冻土导热系数可表示为：

式中：λ*为冻土层等效导热系数（W/（m·K））；C为与土壤含水率和地下水位相关的系数；λe为冻土导热系数（W/（m·K））。

由式（2）可知，只要确定参数C和冻土导热系数λe，就可以计算相应的冻土层等效导热系数λ*。

2.1 基于分形理论的冻土导热系数λe计算公式的建立

1）导热系数分形模型

研究表明，分形理论可用于描述颗粒的形状、运动，分形维数可以用来表征颗粒的随机分散行为，并且在相当宽广的粒度范围内，除了颗粒形状的自相似外，其个数也具有自相似性[11-13]；尽管剖面上的颗粒大小不等、形状各异、随机分布，但与粒径分布、孔隙分布、孔轴分布相似，土壤剖面上颗粒分布同样具有自相似性（图1）[2]，并满足式（3），这为渠道防冻胀研究的冻土导热系数的计算方法提供了新思路。

式中：X为面积度量尺度；S（X）为度量尺度下颗粒平均面积；D为颗粒分布分维；a为比例常数。

我国强冻胀地区常见的粉质黏土样品经过土壤切片处理测量得到样品剖面颗粒分形，见图2。对式（3）取对数，得lnS=lna+DlnX，若具有分形特性，则中间参数lnS和lnX满足线性关系，其中a、D待求。经选取多组度量尺度，粉质黏土样品剖面颗粒分布规律见图3，可求得关系式，即S=0.2866X0.9792。

图1 粉质黏土薄片显微镜观察

图2 剖面颗粒分形

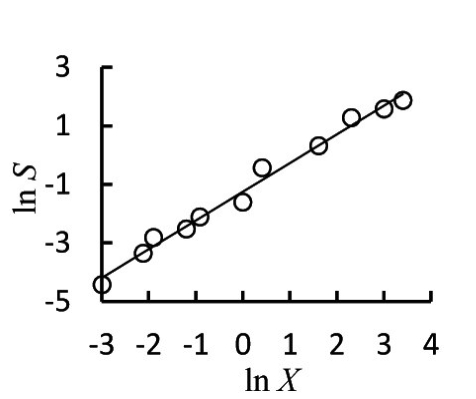
图3 土壤样品剖面颗粒分布规律

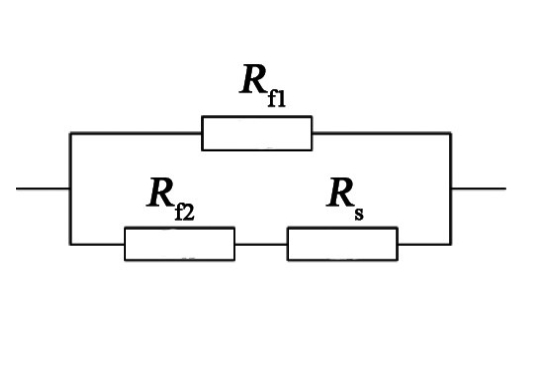
图4 土壤分形结构热阻示意图

2）冻土导热系数计算公式的建立

假定土壤由一个个均匀分布的土壤微结构组成（任意剖面上，S随X的变化而变化，具有自相似性），颗粒间孔隙充斥着流体（空气、水分）。此外，考虑到样品孔隙率适中，进一步假定颗粒间孔隙不连通，忽略孔隙间对流作用及热辐射作用。建立并联传热模型，如图4所示。

式中：Rf1、Rf2分别为通道1、通道2内流体热阻；Rs为通道2内的骨架热阻。

根据传热理论可知：

式中：λe为天然冻土层导热系数，W/（m·K）；λs、λf分别为颗粒、孔隙内流体平均导热系数，W/（m·K）。

借助土壤饱和度Sr、含水率ω、孔隙比e、相对密度ds，可整理得到孔隙内流体平均导热系数λf，即:

同时，引入形状修正系数K，修正大面积度量尺度对应的体积固含率差异：

式中：ε为土壤平均孔隙率；A为剖面颗粒平均投影面积。经计算，K=1.30。

将式（5）—式（10）依次带入式（4），即可求得粉质黏土天然冻土导热系数的分形表达式，即：

其中，土壤饱和度Sr计算式为：

由式（11）和式（12）可知，只要确定含水率ω、孔隙比e和相对密度ds，就可以计算出粉质黏土的天然冻土导热系数。

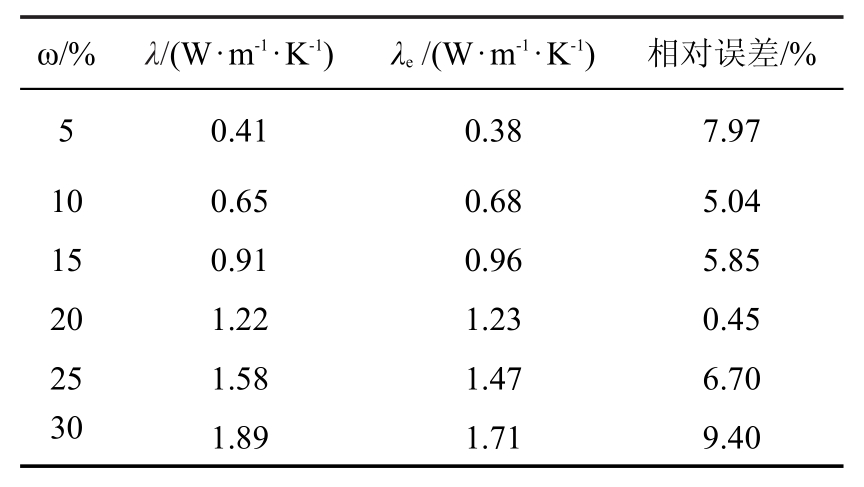
为了验证式（11）的可靠性，通过代入《冻土地区建筑地基基础设计规范》（JGJ118-2011）中给出的粉质黏土的含水率ω、孔隙比e（孔隙率n）、相对密度ds，计算冻土导热系数λe与该规范中计算的粉质黏土冻土导热系数λ进行对比，结果见表1。从表1可以看出，在不同含水率ω取值的情况下，冻土导热系数计算值与规范中给出的计算值基本吻合，最大相对误差为9.40%，证明基于分形理论推导的冻土导热系数计算公式是合理的。

表1 冻土导热系数计算结果

ω/%5 10 15 20 25 30 λ/(W·m-1·K-1)0.41 0.65 0.91 1.22 1.58 1.89 λe/(W·m-1·K-1)0.38 0.68 0.96 1.23 1.47 1.71相对误差/%7.97 5.04 5.85 0.45 6.70 9.40

2.2 系数C的确定

根据黑龙江省万家冻土试验场资料[5]，分析得到C=1/3～1/4，即在强冻胀土等效导热系数取冻土导热系数的1/3～1/4，但在实际应用发现此值偏小，计算的保温层厚度偏大，没有考虑土层含水率和土壤水分迁移的影响；根据华北地区多年试验资料[6]，建立了C与冻土层含水率的关系式，但是没有考虑土壤水分迁移的影响。根据黑龙江蛤蟆通灌区渠道保温防冻胀试验结果，得出C与冻土层冻前含水率和地下水埋深浅时冻结过程地下水的水分迁移有关。现对黑龙江蛤蟆通试验灌区观测的地下水位埋深、含水率及相应的最佳保温方案进行拟合，得到C的计算公式，形如：

式中：hm为地下水位埋深（m），当hm≥2.0m时，取2m；ω为土壤含水率（%）。

C的计算公式（式（13））是根据蛤蟆通灌区渠道保温防冻胀试验结果得出，因此具有一定的适用范围。通过分析，认为该计算公式适用于地下水埋深较浅、渠基土冻结期间存在水分迁移、冻胀较为严重的地区。

2.3 冻土层等效导热系数的计算公式

将式（12）、式（13）代入式（2），整理得冻层等效导热系数计算公式，即：

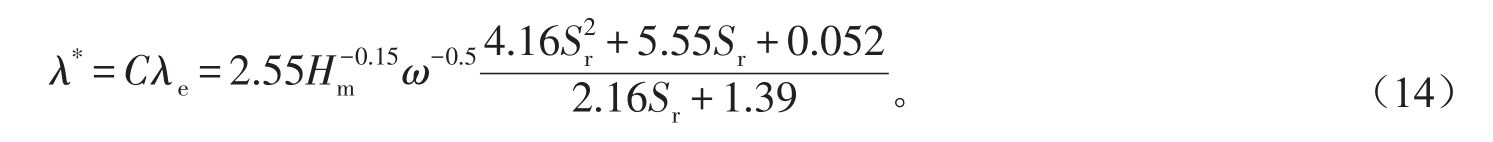
为了验证基于分形理论推导的渠道保温防冻胀冻土层等效导热系数计算公式的可靠性，现利用内蒙古河套灌区、黑龙江蛤蟆通灌区和新疆冲乎尔灌区的渠道保温防冻胀观测资料对式（14）进行验证，渠道保温防冻胀均采用该研究提出的标准化结构型式，计算均选取冻胀最大位置处渠底数据，计算结果见表2。

表2 保温层厚度计算结果

灌区内蒙古河套灌区黑龙江蛤蟆通新疆冲忽尔地下水埋深/m 1.93 4.56 3.25冻胀含水率/%24.39 25.21 25.00混凝土板+砂浆层厚/m 0.08 0.1 0.08混凝土导热系数λh/(W·m-1·K-1)1.58 1.58 1.58苯板导热系数λs/(W·m-1·K-1)0.044 0.044 0.044设计冻深Z/m 1.10 1.98 1.56试验段最佳厚度S/m 0.06 0.12 0.1计算厚度S/m 0.064 0.118 0.093相对误差/%6.67 1.67 7.00

内蒙古河套灌区、黑龙江蛤蟆通灌区和新疆冲乎尔灌区均为我国北方强冻胀地区。由以上公式得到的渠道等效导热系数的计算方法，计算得到的聚苯乙烯保温板厚度均与试验段最佳厚度接近，最大相对误差仅为7.00%，说明其计算精度较高，能满足渠道保温防冻胀设计中保温板厚度的计算要求。

3 粉土及粉质黏土常用冻土层等效导热系数

由式（14）可知，若已知土壤含水率ω、孔隙比e、相对密度ds和地下水埋深，即可求出冻土层等效导热系数λ*。粉土及粉质黏土是我国寒冷地区常见的冻胀性较强的土壤，现将利用式（14）计算得到的粉土及粉质黏土不同含水率和不同地下水埋深情况下的冻土层等效导热系数λ*计算结果列于表3，实际工程应用中可以根据渠道基土的具体情况进行选用。

表3 粉土及粉质黏土常用冻土层等效导热系数

ω/%λ/(W·m-1·K-1)λe/(W·m-1·K-1)不同埋深下等效导热系数λ*/(W·m-1·K-1)5 10 15 20 25 30 5 10 15 20 25 30 5 10 15 20 25 0.35 0.57 0.79 1.06 1.39 1.68 0.41 0.65 0.91 1.22 1.58 1.89 0.46 0.74 1.02 1.38 1.80 0.31 0.57 0.80 1.02 1.23 1.43 0.38 0.68 0.96 1.23 1.47 1.71 0.45 0.82 1.15 1.47 1.76 0.5m埋深0.23 0.30 0.34 0.38 0.41 0.44 0.28 0.36 0.41 0.46 0.49 0.52 0.34 0.43 0.50 0.55 0.59 1.0m埋深0.26 0.33 0.38 0.42 0.46 0.48 0.31 0.40 0.46 0.51 0.54 0.58 0.37 0.48 0.55 0.61 0.65 1.5m埋深0.27 0.35 0.41 0.45 0.48 0.51 0.33 0.42 0.49 0.54 0.58 0.61 0.40 0.51 0.58 0.65 0.69≥2.0m埋深0.28 0.37 0.42 0.47 0.50 0.54 0.35 0.44 0.51 0.56 0.60 0.64 0.41 0.53 0.61 0.67 0.72

4 结论

1)针对北方寒冷地区建立了渠道保温防冻胀的冻土层等效导热系数计算公式λ*=Cλe，基于分形理论建立了由含水率计算冻土导热系数λe的计算公式，经验证和规范中粉质黏土的冻土导热系数值相比变化规律吻合度高，最大相对误差为9.40%；根据黑龙江蛤蟆通灌区渠道保温防冻胀试验结果，得出C与冻土层冻前含水率和地下水埋深浅时冻结过程地下水的水分迁移有关，用灌区观测的地下水位埋深、含水率及相应的最佳保温方案进行拟合，得到C的计算公式，进而得到可直接计算冻土层等效导热系数λ*。

2）结合灌区的试验观测结果，对提出的冻土等效导热系数的计算公式进行验证，得到的渠道保温层的厚度计算值与3个灌区最经济安全的保温层厚度相比，最大相对误差为7.00%，说明提出的冻土层等效导热系数λ*的计算公式可在渠道防冻胀技术保温层厚度的计算中应用推广。

3）根据冻层等效导热系数计算公式（式（14）），测定含水率ω、孔隙比e、相对密度ds和地下水埋深，即可求出冻土层等效导热系数λ*，该公式适用于地下水埋深较浅、渠基土冻结期间存在水分迁移、冻胀较为严重的地区。常用粉土及粉质黏土冻土层等效导热系数列于表3，实际工程应用中可以根据渠基土的具体情况进行选用。

参考文献：

[1]宋珲，朱明．季节性冻土地区路基的冻胀与融沉[J]．路基工程，2007（1）：26-28．

[2]李书民，李振卿．南水北调工程防冻胀保温层厚度计算方法讨论[J]．河北水利水电技术，2000(3):53-55.

[3]郭殿祥,马移军．保温法防冻胀设计中的参数取值方法[J]．防渗技术，1999.5(2):45-47.

[4]安鹏，邢义川．基于部分保温法的渠道保温板厚度计算与数值模拟[J]．农业工程学报，2013,29(17):54-62.

[5]宋清林，何武全，李根等．混凝土衬砌渠道保温防冻胀技术研究[J]．灌溉排水学报，2015,34(4):43-48.

[6]李根，何武全，宋清林等．混凝土衬砌渠道置换防冻胀标准化技术模式[J]．节水灌溉，2015(4):79-83.

[7]程满金，申利刚．聚苯乙烯保温板在衬砌渠道防冻胀中的应用研究[J]．灌溉排水学报，2011,30(5):22-26.

[8]陈永平，施明恒．基于分形理论的多孔介质导热系数研究[J]．工程物理学报，1999,9(5):602-608.

[9]徐琳，张旭．土壤样品有效导热系数的分形计算模型[J]．可再生能源，2009,2(1):81-87.

[10]张宇峰．渠道防渗保温防冻胀技术标准化模式研究[D]．杨凌：西北农林科技大学，2014.

[11]TOVEY N K.ADigital Computer Technique forAnalysis of Micro-graphs of Soil Fabric[J].Journal of Microscopy,1990,120:303-305.

[12]TYLER S W,Wheatcraft S W.Fractal scaling of soil particle-size distributions:analysis and limitations[J].Soil Science Society of America Journal,1992,56(2):362-369.

[13]CHEN Huie,WANG Qing.The Behavior of Organic Matter in the Process of Soft Soil Stabilization Using Cement[J]．Bulletin of Engineering Geology and the Environment,2006,65:445-448.

[14]SL23-2006，渠系工程抗冻胀设计规范[S]．

Calculating the Effective Thermal Conductivity Coefficient of the Frozen Layerin Thermal-conservative and Freezing-resistant Cannel

ZHANG Yufeng1,HE Wuquan2,ZHAO Yanlin1
(1.Yangling Vocational&Technical College,Yangling 712100,China；2.College of Water Resources andArchitectural Engineering,NorthwestA&F University,Yangling 712100,China）

Abstract:Empirical methods commonly used for calculating the effective thermal conductivity coefficient of the frozen layer in thermal-conservative and freezing-resistant cannels could give rise to considerable errors.To overcome this problem,we proposed a fractal-based model in this paper to calculate effective thermal conductivity coefficient of silty clay in permafrost in the cold region of northern China.We calculated the coefficient C using data obtained from Ha Matong Irrigation District and then applied and tested the model against data obtained from-Hetao Irrigation District in Inner Mongolia,Chong Huer Irrigation District in Sinkiang,and Ha Matong Irrigation District in Heilongjiang.The results showed that the calculated thickness of polyphenyl plate was almost the same as the optimal thickness with an error of just 7.0%,proving the accuracy of the model.We also calculated the effective thermal conductivity coefficient of silt and silty clay in permafrost.The model can be used in regions where groundwater table is shallow and there is soil water movement when soils are freezing with prolonged frost heaves.

Key words:anti-seepage channels;heat preservation and frozen prevention;fractal theory;effective thermal conductivity coefficient.

中图分类号：S277；TV315

文献标志码：A

doi：10.13522/j.cnki.ggps.2017.06.013

责任编辑：刘春成

张宇峰，何武全，赵彦琳.渠道保温防冻胀中冻土层等效导热系数的计算[J].灌溉排水学报，2017,36（6）：69-73.

文章编号：1672-3317（2017）06-0069-05

收稿日期：2016-10-15

基金项目：国家“十三五”重点研发计划课题（2016YFC0400203）；水利部科技推广计划项目（TG1214）

作者简介：张宇峰（1987-），男，河北张家口人。助教，硕士，主要从事节水灌溉理论与技术研究。E-mail:848792382@qq.com