西北寒旱灌区裸露地表粗糙度SAR反演建模方法研究①

王 学，刘全明，马 腾

（内蒙古农业大学 水利与土木建筑工程学院测绘工程系， 呼和浩特 010018）

摘 要：快速获取大范围土壤地表粗糙度的空间分布是一个急需解决的科学难题。以快速获取内蒙古河套灌区解放闸灌域土壤地表粗糙度为目的，研究了RADARSAT-2雷达影像数据的地表粗糙度信息提取技术，通过剖面板法实测地表粗糙度数据。利用BP（Back Propagation）人工神经网络和LMBP（Levenberg-Marquardt Back Propagation）人工神经网络模型2种方法建立了土壤地表粗糙度的定量反演模型，并对模型进行验证。结果表明，LMBP模型的反演效果优于BP模型，其决定系数R2分别为0.888 3、0.689 2。建立的雷达后向散射系数反演土壤地表粗糙度的人工智能模型，能够在一定程度上满足快速获取土壤地表粗糙度的需要，为微波遥感监测土壤墒情及土壤盐渍化提供重要基础参数。

关键词：地表粗糙度；神经网络；SAR；模型

0 引言

地表粗糙度对电磁波反射具有显著影响，因此在微波遥感反演土壤水分的研究中，地表粗糙度是影响后向散射的重要因素，成为遥感研究的焦点之一[1-5]。遥感技术，尤其是合成孔径雷达（SyntheticAperture Radar，SAR）的快速发展，为大面积获取寒旱区地表粗糙度信息提供了定量化的研究手段[6]。

自然地表几何特征十分复杂，且表面随机分布，无法建立完美的模型来模拟所有散射情况。往往通过理论、经验或者半经验模型雷达数据进行解译，从而得到有用信息。理论模型中应用最广的是积分方程Integral Equation Models（IEM）[7]，但该模型存在着不能准确刻画实际地表粗糙度和菲涅尔（Fresnel）系数在各种地表情况下只能进行简单处理的2大问题。导致在自然地表应用该模型时，后向散射系数的模型反演值与实测值难以取得较好的相关性[8-10]。经验模型没有理论上的广泛支持，从而使模型没有大的适用范围，因此一些研究人员提出了Dubois模型[11]和OH模型[12]等半经验模型来兼顾二者的优点，但是2个模型中也存在着2点不足：一是只有表面均方根高度参与建模，真实地表的后向散射特征不能在理论上得到准确地描述。二是在小范围内通过实测地表数据建立的模型，有较强的依赖性，不具有广泛性。

许多从事微波定量反演的科研人员针对不同的地表类型，对上述模型进行了改良利用。孔金玲等[13]用新的组合粗糙度参与微波遥感水分反演；廖静娟等[14]利用SAR数据结合遗传算法和后向散射模型反演了额济纳冲积扇的地表参数；林国青等[15]基于SAR数据的干旱区冲积扇地表粗糙度反演。Baghdadi等[16]通过对均方根高度S和相关长度L定标，建立了二者的经验关系，使IEM模型的模拟后向散射系数与真实值更加接近。虽然SAR反演建模能够得到地表粗糙度参数，但是针对西北寒旱灌区裸露地表粗糙度的反演却缺乏相应的研究，并且现有模型得到的结果并不是十分的理想。

近些年，神经网络模型被逐步引入微波遥感反演地表粗糙度中，与理论模型和经验模型相比较，神经网络模型不受地域及地表参数的限制，反而能得到较好的反演结果。2002年，杨虎等[17]利用神经网络与雷达参数相结合的方法进行地表参数反演，结果和实际情况较为吻合。为此，通过对比常规经验模型，研究建立LMBP[18]人工神经网络模型，以多波段、多极化雷达影像后向散射系数值作为神经网络参数值，对网络训练并优化训练参数，实现对地表粗糙度的反演，以提高地表粗糙度反演精度。土壤地表粗糙度作为土壤地表水盐反演的一个重要参数，为开展寒旱地区水盐反演研究工作提供有效的信息支持[19]。

1 试验区概况与SAR数据

1.1 试验区概况

试验区位于河套灌区解放闸灌域内，地处内蒙古自治区巴彦淖尔市杭锦后旗境内，北靠阴山，东郊临河市，南望鄂多斯高原，西与磴口接壤，是典型引黄河水灌溉的旗县。海拔1 033～1 055m，属温带高原型、大陆性气候，全年平均气温6.3～7.7℃，干燥少雨，全年平均降雨量为139.4mm，平均蒸发量达2 070.4mm，解放闸灌域的复杂环境系统，使其成为理想的试验区域。

1.2 Radarsat-2C波段影像数据

作为当今世界十分先进的SAR系统，Radarsat-2具有成像模式多、分辨率高、成像幅宽大、视角范围广等特点，可在大范围内快速成像，减少卫星过境时间。与此同时还有多种极化方式可供选择，提高了对目标物进行精细刻画的能力[20]。

研究使用C波段Radarsat-2的HH+HV+VH+VV精细全极化模式的雷达影像，其中H代表水平极化方式，V代表垂直极化方式，二者相结合。其影像采用SLC（Single Look Complex）模式，即单式复型模型，影像数据经过处理后，很好地保留了SAR的信息[21]。

通过雷达影像处理软件ENVI SARscape来处理获取的Radarsat-2的雷达数据，数据处理主要包括以下内容：数据聚焦、多视处理、斑点滤波、地理编码和辐射定标、几何校正、提取后向散射系数[22]。如表1所示部分采样点的后向散射系数值。

表1 部分采样点后向散射系数值

2 地表粗糙度数据

地表粗糙度通常被当作静态且随机的地表用于微波散射模型建模[23]，因此用地表均方根高度S、自相关函数和相关长度L这3个统计变量对地表粗糙度特征进行定义，其中均方根高度S从垂直尺度、相关长度L从水平尺度分别对地表粗糙度进行了表达。

2.1 均方根高度S

将地表面假设在x-y坐标系内，其中某点的高度为z(x，y)，在坐标系内上取一块中心处于原点的表面并使其具有统计意义，坐标数值分别为Lx和Ly，则该表面的平均高度为：

其二阶矩为：

表面高度的标准偏差（均方根高度）S就为：

对于一维离散数据，表面高度的标准偏差（均方根高度）S为：

式中N为采样点的总数目。

2.2 相关长度L

对于一维离散数据z(x)，其归一化自相关函数r为：

r是描述点x的高度z(x)与另一点X´的高度Z(x±x´)之间相关性的一种度量，对离散数据来说，点x´=(j-1)x（j为自然数）的自相关函数，即：

当自相关函数r(x´)的值恰为1/e时所对应的间隔x´则被称为相关长度L。

2.3 表面自相关函数

通常用高程的概率分布函数或表面自相关函数作为描述随机地表的传统方法，并且假定其高程服从高斯分布，则表面自相关函数通常用高斯自相关函数或指数自相关函数来表示。

1）高斯自相关函数

2）对于各向同一性的一维随机地表单参数指数自相关函数为：

2.4 测量地表粗糙度

带有厘米格网的剖面板测量法、带有探针的针式板测量法以及带有激光扫描仪的光电测量法是主要的地表粗糙度的测量法。考虑价格低廉、便于携带、测量速度快且效果好等因素，选择使用带有厘米格网的剖面板方法测量地表粗糙度，具体步骤为：

1）试验采用雷达影像的像元为8m×8m，在每个采样点上进行5处数据的重采样工作，分别对应4个角点及中心点，取其平均值作为每一个像元点的地表粗糙度。

2）将带有厘米格网剖面版按照1∶100的比例在南方Cass软件中进行缩放，然后将拍摄的照片按照线性变换规则进行几何校正；通过使用多段线将地表的起伏进行描绘，如图1红色曲线所示。

3）按采样间隔1cm对几何校正后的剖面数据（图1几何校正后图像）量取相对高度，获得其离散样点的相对高度值，将数据保存在Excel表格中。

4）根据均方根高度S计算公式（4）及表面相关长度L计算公式（6）用Matlab编程软件对数据进行编程，通过Excel批量导入数据，自动计算地表参数，并绘制出自相关函数图谱（图2、图3），按照以上步骤获得全部采样点数据（表2）。当相关函数r(x´)与直线L=1/e相交时所对应的距离就是该点的表面相关长度L。

图1 几何校正后图像

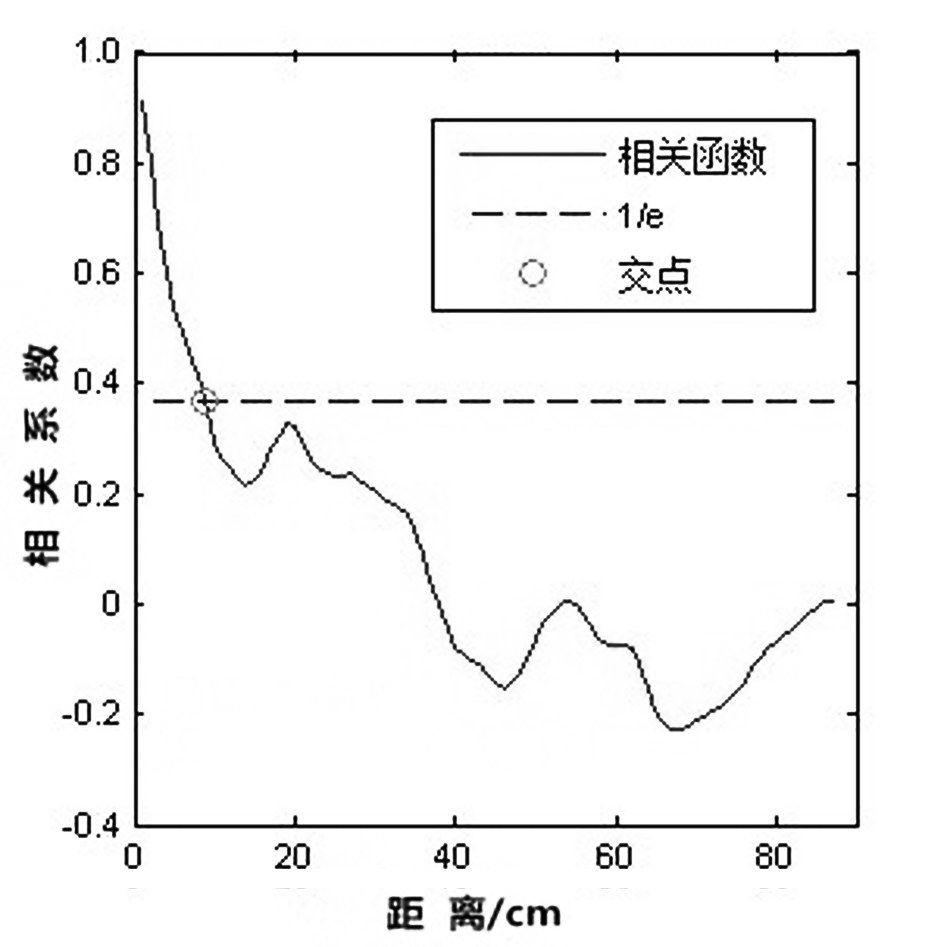
图2 13号点自相关函数图谱

图3 20号点自相关函数图谱

表2 部分地表粗糙度实测数据

3 模型研究

地表粗糙度反演模型的初期研究只有均方根高度S或相关长度L之一参与模型运算，不能得到较好的反演结果，科研人员通过对S和L进行组合来表示地表粗糙度，如Shi等[24]的研究中釆用波数k、S与粗糙度谱W组成SR=(kS)2W，Oh等[25]利用L与S组成S/L，而Zribi等[26]利用S与L组成ZS=S2/L，他们采用的组合参数在模型反演中均取得了理想效果。兹将利用组合参数ZS进行反演建模。

3.1 BP神经网络

BP神经网络采用迭代训练，当均方误差达到预期值时就会预中止迭代过程。土壤的表面粗糙度与雷达后向散射系数之间存在着复杂的相关性，通过BP神经网络技术可以研究其相关性的逼近问题，为地表粗糙度反演建模提供了新思维与新方法。根据研究问题的需要确定BP神经网络中输入层及输出层的单元数目，然而对于隐含层的单元数目的确定目前则无现成的公式可用。其BP模型结构主要如下：

1）输入层、双隐含层和输出层组成4层网络结构，进行BP神经网络模型的构建。

2）HH、HV、VH、VV极化的后向散射系数作为输入层的4个单元；通过对选定后的参数进行经多次反复计算最终定2个隐含层，2个隐含层中均有35个节点；组合地表粗糙度ZS作为输出层。

3）该网络中隐含层的传递函数选择Sigmoid函数，输出层选择Purelin函数，使整个网络的输出可以取任意值，训练函数Tansig进行网络的训练。

BP模型通过100个采样点的400个全极化后向散射系数数据与100个组合粗糙度数据共500个数据作为训练数据进行训练建模，55个点共275个数据进行验证，迭代次数20 000次，允许误差0.000 1。

3.2 LMBP神经网络

因为BP算法是使用最速下降法的传统标准算法，受其算法本身的限制，故BP神经网络的收敛速度比较慢，LMBP算法通过提高其收敛速度对传统BP算法的改进，其算法不仅具有快速收敛性，还具有整体收敛特性，是最速下降法与牛顿法相结合的算法。兹LMBP神经网络模型同样由输入层、双隐含层和输出层组成。其网络结构与BP网络结构是一样的，只是第1隐含层有8个节点，第2隐含层有8个节点，本模型最大迭代次数1 000次，允许误差0.000 5。

4 结果与分析

为进行神经网络建模，兹通过编程软件MATLAB的工具箱编写BP与LMBP神经网络程序，因采样点数目有限，将100个采样数据作为训练数据，构建4层神经网络模型，并选用Tansig函数进行网络训练，当达到预期误差后，用剩余55个采样数据（检验点占比35%）进行外部检验。并绘出BP与LMBP模型预计值与样本值对比图、相关性分析图。

图4 LMBP模型模拟数据与实测数据相关性分析

图5 BP模型模拟数据与实测数据相关性分析

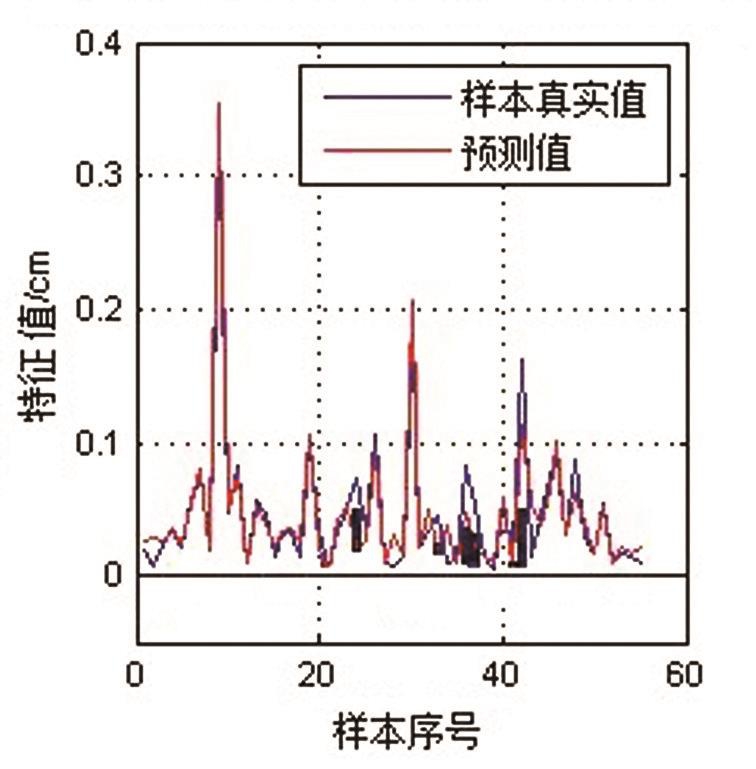
图6 LMBP模型预计值与样本值对比

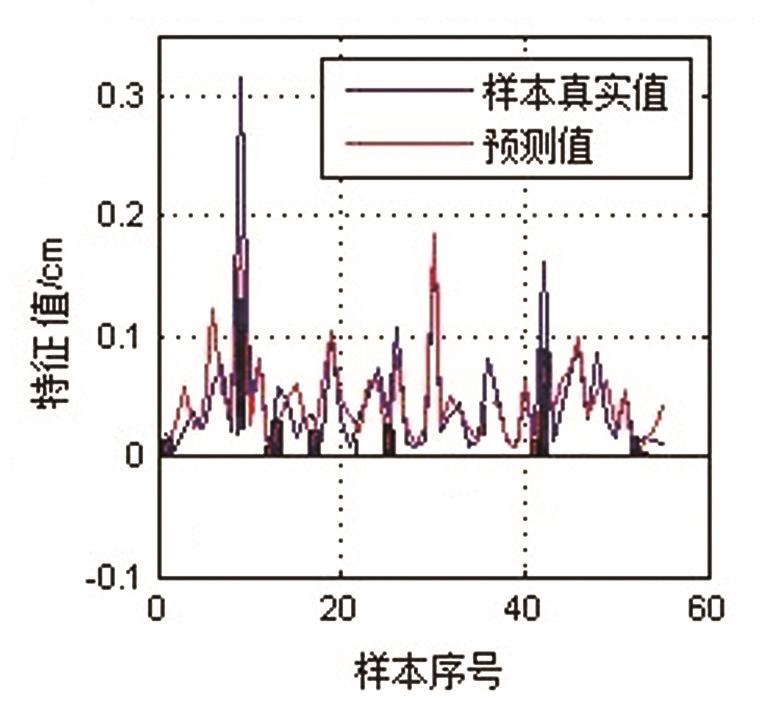
图7 BP模型预计值与样本值对比

图4中地表粗糙度LMBP神经网络模型决定系数R2=0.888 3，并发现数据均匀分布于直线二侧，基本上没有较离散数据；图5中地表粗糙度BP神经网络模型决定系数R2=0.689 2，并发现虽然数据均匀分布与直线的二侧，但是存在离散数据；通过对二者相关性对比分析发现LMBP神经网络模型的决定系数明显大于BP神经网络模型的相关系数，由于决定系数越接近1，相关性越密切，因而可以得出LMBP模型的预测值比BP模型的预测值更加与实测值接近；图6中LMBP模型验证数据预计值与样本值的对比分析发现，红色预测值与蓝色真实值的峰值波动基本吻合没有较大差值；图7中BP模型验证数据预计值与样本值的对比分析发现，红色预测值与蓝色真实值的峰值波动有较多不吻合的地方，存在较多的差值；因此通过对以上2种结果数据的对比分析发现LMBP神经网络对地表粗糙度的反演效果要优于BP神经网络的反演效果。

5 结论

通过河套灌区解放闸灌域春灌前的四极化Radarsat-2的雷达数据，采用剖面板法获取试验区内155个采样点的地表粗糙度数据，采用BP神经网络和LMBP神经网络方法建立了土壤地表粗糙度的定量遥感反演模型。得到以下结论：

1）采用剖面板法获取粗糙度参数，通过均方根高度S和相关长度L构成组合粗糙度参数ZS参与神经网络模型运算，得到的数据结果表明此方法是可行的，可以对西北裸露地表粗糙度情况进行表达。

2）100个采样点雷达后向散射系数与组合粗糙度ZS参与建模，50个采样点雷达后向散射系数与组合粗糙度ZS参与模型验证，得到LMBP网络模型反演结果相关系数为0.888 3，BP网络模型反演结果决定系数为0.689 2，二者的相关系数均大于0.5，表明神经网络模型较好的匹配了地表粗糙度与雷达后向散射系数之间的特征关系，但是LMBP网络模型反演结果决定系数大于BP网络模型反演结果决定系数，并且LMBP神经网络模型的反演效果要优于BP神经网络模型。

3）LMBP人工智能模型反演地表粗糙度，充分考虑了各项地表参数，无须复杂的介电常数模型，只需建立后向散射系数与地表参数关系，可为接下来进行的土壤墒情以及土壤盐渍化监测反演模型的建立提供数据支持。

兹只是通过剖面版获取粗糙度数据，没有与激光扫描等方法获取的数据进行对比，可能存在原始数据误差的问题，对地表粗糙度的反演精度产生一定的影响，也没有考虑介电常数的问题，这些都是今后应研究并解决的问题。

参考文献:

[1]LIEVENS H,VERHOEST N,KEYSER E D,et al.Effective roughness modelling as a tool for soil moisture retrieval from C-and L-band SAR[J].Hydrology and Earth System Sciences Discussions,2010,7（4）：4 995-5 031.

[2]LIEVENS H,VERNIEUWE H,A LVAREZ-MOZOS J,et al.Error in SAR derived soil moisture due to roughness parameterization:An analysis based on synthetical surface profiles[J].Sensors,2009,9：1 067-1 093.

[3]GORRAB A,ZRIBI M,BAGHDADI N,et al.Retrieval of both soil moisture and texture using Terra SAR-X images[J].International Journal of Remote Sensing,2015,7:10 098-10 116.

[4]JAGDHUBER T,HAJNSEK I,PAPATHANASSIOU K P.An iterative generalized hybrid decomposition for soil moisture retrieval under vegetation cover using fully polarimetric SAR[J].IEEE Journal of Selected Topics in Applied Earth Observations and.Remote Sensing，2015,8:3 911-3 922.

[5]NOTARNICOL A C.A bayesian change detection approach for retrieval of soil moisture variations under different roughness conditions[J].IEEE Geoscience and Remote Sensing Letters,2014,11:414-418.

[6]曾珍,杨本勇,范建容,等.基于地表粗糙度地学意义的地表真实面积计算[J].遥感技术与应用，2014,29（5）：846-852.

[7]FUNGAK，CHEN K S.An update on the IEM surface backscattering model[J].IEEE Geoscience and Remote Sensing Letters,2004,2（1）：75-77.

[8]BAGHDADI N,GHERBOUDJ I,ZRIBI M,et al.Semiempirical Calibration of the IEM Backscttering Model Using Radar Imagesand Moisture and Roughness Field Measurements[J].International Journal of Remote Sensing,2004,25（18）：3 593-3 623.

[9]BAGHDADI N,HOLAH N,ZRIBI M.Soil Moisture Estimation Using Multiincidence and Multipolarization ASAR Data[J].International Journal of Remote Sensing,2006,27（10）：1 907-1 920.

[10]DHARSSI I,BOVIS K J,MACPHERSON,B,et al.Operational assimilation of ASCAT surface soil wetness at he Met Office[J].Hydrology and Earth System Sciences Discussions,2011,15（8）：2 729-2 746.

[11]DUBOIS P C,VAN ZYL J,ENGMAN T.Measuring Soil Moisture with Imaging Radars[J].IEEE Transactions on Geoscience and Remote Sensing,1995,33（4）：915-926.

[12]OH Y,SARABANDI K,ULABY F T.Semi-empirical Model of the Ensemble Averaged Differential Muller Matrix for Microwave Backscattering from Bare Soil Surfaces[J].IEEE Transactions on Geoscience and Remote Sensing,2002,40（6）：1 348-1 355.

[13]孔金玲，甄佩佩等.基于新的组合粗糙度参数的土壤水分微波遥感反演[J].地理与地理信息科学,2016,5（3）:34-38.

[14]廖静娟，庞自振.多极化SAR数据反演额济纳冲积扇地表参数[J].地球信息科学学报，2009,11（1）：77-83,131.

[15]林国青，郭华，张东露.基于SAR数据的干旱区冲积扇地表粗糙度反演[J].遥感技术与应用，2013，8（4）：660-665.

[16]BAGHADAI N,CHAAYA J A,ZRIBI M.Semi-empirical calibration of the integral equation model for SAR data in C-band and cross polarization using radar images and field measure-ments[J].IEEE Geoscience and Remote Sensing Letters,2011,8（1）：14-18.

[17] 杨虎，郭华东，王长林，等.基于神经网络方法的极化雷达地表参数反演[J].遥感学报，2002，6（6）：451-455.

[18]赵旭峰.LMBP神经网络算法改进及其应用[D].北京：中国科学技术大学,2014.

[19]SHI J C，DU Y，DU J Y，et al.Progresses on microwave remote sensing of land surface parameters[J].Science in China Series B,Chemistry,life sciences&Earth Sciences，2012，5（5）:1 052-1 078.

[20]RADARSAT-2卫星介绍[J].中国科学院对地观测与数字地球科学中心用户简讯,2008,(73).

[21]马腾，王耀强，李瑞平，等.基于微波遥感极化目标分解的土地覆盖/土地利用分类[J].农业工程学报，2015,31（2）：259-265.

[22]MOZOS J A,CASALI J,AUDIACANA M G,et al.Correlation be-tween ground measured soil moisture and RADARSAT－1derived backscattering coefficient over an agricultural catchment of Navarre(north of Spain)[J].Bioprocess and Biosystems Engineering，2005，92（1）：119-133．

[23]MORENO R G，LVAREZ M D，ALONSO A T，et al.Tillage and soil typeeffects on soil surface roughness at semiarid climatic conditions[J].Soil and Tillage Research,2008,98:35-44．

[24]SHI J,CHEN K S,VAN ZYL J,et al.Estimate relative soil moisture change with multi-temporal L band radar measurements[C]//IEEE International Geoscience and Remote Sensing Symposium,2002,1:647-649.

[25]ISOK O H.Quantitative and retrieval of soil moisture content and surface roughness from multipolarized radar observations of bare soil surfaces[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42（4）:596-601.

[26]ZRIBI M,HE´GARAT-MASCLE S L,OTTL´E,et al.Surface soil moisture estimation from the synergistic use of the(multi-incidence and multi-reso lution)active microwave ERS Wind Scatterometer and SAR data[J].Remote Sensing of Environment,2003,86（1）：30-41.

Inversely Calculating the Roughness of Bare Soil Surface in Cold-arid Irrigation Regions Using the SAR Method

WANG Xue,LIU Quanming,MATeng
(Department of Surveying and Mapping Engineering in Water Conservancy and Civil Engineering Institute,Inner MongoliaAgricultural University,Hohhot 010018,China)

Abstract：Quick calculation of spatial distribution of soil surface roughness is important both practically and scientifically.In this paper we investigated the feasibility of using the radar image of RADARSAT-2to inversely calculate the surface roughness of Jiefangzha Irrigation area in Hetao Irrigation District of Inner Mongolia.The surface roughness in the radar image was calculated by the sectional plate method.We used both back propagation(BP)artificial neural network and the Levenberg-Marquardt back propagation(LMBP)artificial neural network to calculate and verify the inverse model for quantifying the surface roughness.The results showed that the LMBP model was superior to the BP model,witha R-squared coefficient of 0.888 3and 0.689 2respectively.Calculating soil surface roughness inversely using artificial intelligent model and the radar backscatter coefficient is quick,providing important basic parameters for using microwave remote sensing to monitorsoil moisture and soil salinization.

Key words:soil surface roughness;LMBP neural network;SAR;modeling

中图分类号：S152.7；P628.2

文献标志码：A

doi：10.13522/j.cnki.ggps.2017.06.014

责任编辑：赵宇龙

王学，刘全明，马腾.西北寒旱灌区裸露地表粗糙度SAR反演建模方法研究[J].灌溉排水学报，2017，36（6）：74-80.

文章编号：1672-3317（2017）06-0074-07

收稿日期：2016-09-27

基金项目：国家自然科学基金项目(51569018，51249007)；内蒙古自然科学基金项目（2013MS0609）；“十三五”国家重点研发计划项目（2016YFC0501301）

作者简介：王学（1991-），男。硕士研究生，主要从事测绘工程教育与定量遥感反演理论及应用研究。E-mail：sdzqwx@126.com

通信作者：刘全明（1973-），男。副教授，硕士生导师，博士，主要从事测绘工程教育与定量遥感反演理论及应用研究。E-mail：nndlqm@sina.com