陈学军1，姜宝良2，张晓偲2
(1.济源职业技术学院，河南济源454650；2.华北水利水电大学，郑州450016）
摘 要：受土壤有机质和微生物的影响，大部分农业土壤都有团聚体结构。团聚体内部的孔隙一般很小，与团聚体之间的水流相比，团聚体内部的水可以视为不动的。但受质量浓度梯度和分子扩散的影响，2个水体内的溶质可以相互交换。模拟溶质在具有团聚体结构土壤中运移时，溶质在以上2个水体间的交换过程常用可动-不可动水体模型来描述。土壤溶质运移涉及的参数较多，很多参数不能直接测定，要靠观测值拟合才能获得。由于不同的参数组合可以得出相同溶质质量浓度分布，因此，即使模拟结果和实验结果吻合也不能确保该模型正确描述了2个水体之间的溶质交换过程。为了深入研究这一问题，利用三维图像技术和数学模型，计算了团聚体内外溶质交换速率。结果表明，Coats-Smith模型误差很大，2个水体之间的溶质交换速率并非与其质量浓度差成正比。作为改进，提出并证明广义γ分布函数可以准确地描述团聚体内外溶质交换过程。
关键词：溶质运移；X射线扫描；土壤；团聚体；可动-不可动水体模型；记忆函数
水分和溶质在土壤中的运移是很多领域的一个普遍现象。在农业、水文、环境领域，污染物在土壤中的运移和转化、污染土壤的改良修复以及植物根系对水分和养分的吸收等过程都与土壤溶质运移有关[1]。因此，如何定量模拟不同条件下水分和溶质的运移转化受到了国内外广泛重视[2-3]。模拟水分和溶质在土壤中运移的数学模型以宏观模型为主[2,4]。在宏观模型中，土壤孔隙结构和孔隙内部发生的所有物理和化学过程通过空间平均的方法参数化。例如，不同土壤孔隙结构对水分运动的影响用水力传导系数表示，而对溶质的影响用弥散系数表示[5]。宏观尺度下观测到的所有水盐运动现象都是孔隙尺度下水盐运动的结果，取决于土壤的孔隙结构。研究孔隙尺度下的水盐运动过程对于改进宏观模型至关重要，自20世纪50年代起，就受到了广泛的关注[6-9]。
团聚体内的孔隙一般在纳米和微米之间，而团聚体之间的孔隙则可以达到几个毫米[10-11]。由于土壤团聚体内外的孔隙尺寸相差如此之大，水分在团聚体内运动要比在团聚体外的运动慢得多，因此，在模拟土壤水分运动时，团聚体内的水一般认为是静态的。对于可溶性化学物质，由于受质量浓度梯度和分子扩散的影响，团聚体内外的溶质可以相互交换。早期模拟具有团聚结构土壤中溶质运移的模型为二区模型[3]或优先流动模型[12]，该模型假定溶质在水体内的交换速率与2个水体内中的质量浓度差成正比[13]，其比例系数称为质量交换系数。在实际应用中发现，对同一土壤，该模型的质量交换系数要随土壤水的流速而变化，才能拟合观测数据[17]。因为目前尚无理论依据证明质量交换系数应随土壤水流而变，普遍认为传统的二区和优先流动模型过于简单，不能正确描述溶质在土壤团聚体内外的交换过程[14]。如何描述这一物质交换过程是土壤学和水文学中仍然没有很好解决的一个问题[14]。一般用记忆函数模型来描述这一物质交换过程[14]，常用的记忆函数有指数函数和伽马函数[15]。由于可动与不可动水体间溶质的交换速率不能实际观测，这些记忆函数是否正确描述了这一物质交换过程仍是一个没有解决的问题[16]。近年来，三维图像技术，特别是X-射线扫描仪在土壤研究中得到了广泛的应用[11]。三维图像的精度可以达到几个微米，可以精确测定非扰动土内团聚体的形状、排列和扩散性能。兹将三维成像技术和孔隙尺度模型结合，首次直接计算可动与不可动水体间的溶质交换速率，利用模拟结果，对常用的模型进行了评估。
以溶质在土壤剖面上的一维运动为例，可动-不可动水体模型可以用如下的方程描述[2]：
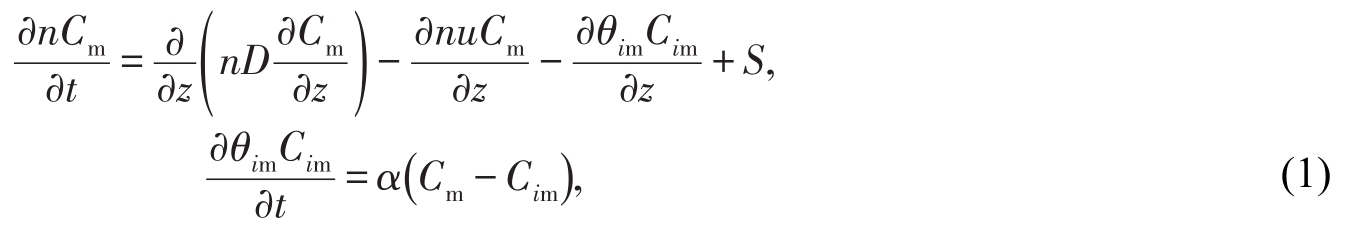
式中：n为团聚体间孔隙的孔隙率；Cm为团聚体间溶质的平均质量浓度(mg/L)；Cim为团聚体内溶质的平均质量浓度(mg/L)；D为水动力学弥散系数(cm2/s)；u为团聚体间的平均水流速度(cm/s)；θim为团聚体内的孔隙率；α为团聚体内外溶质的交换速率常数(s-1)；S为源汇项(mg/(L·s))。
如果团聚体内的初始溶质质量浓度为0，对式（1）中的第二式进行拉普拉斯变换后可消掉Cim，结果为：
式（2）可以写成如下一般的形式：
式中：g（t）一般称为记忆函数（Memory function)[14]。与式（1）对应的记忆函数为指数分布函数：
常用的记忆函数还有伽玛函数等[15]。将式（3）代入式（1）得：
对于不参与化学反应的溶质，g(t) 是一个概率密度函数
对于参与化学反应的溶质，式（3）仍适用，但
本文只研究不参与任何化学反应的溶质。
除上述的指数分布函数和伽玛分布函数外，在过去几十年的研究中，研究人员还提出了其他形式的记忆函数[14,16]。由于这些函数都是经验函数，其中的参数值要靠与实测质量浓度拟合才能确定。因此，即使这些函数的模拟结果能很好地拟合试验数据，也不能代表他们正确地描述了团聚体内外的溶质交换过程。因此，研究溶质在土壤团聚体内外2种水体之间的交换机理、进而提高模型的精确度，对农业中的精准灌溉施肥有重要意义。
研究所用土壤取自于澳大利亚昆士兰东南部的沃里克。这是一种富含蒙脱石的土壤，含黏土量为44.2%，总有机碳量为2.25%，土壤孔隙率为36.2%[18]。为了测定土壤团聚体结构，分别对原状土和扰动土进行了三维X-射线扫描测定，图像的分辨率为30 μm。为了便于理解土壤团聚体的内部结构，图1给出了土壤的二维灰色图片，其中团聚体大小和分布清晰可见。在数值模拟中，需先对灰色图片进行数字化，在数字化的土壤图像中，用1代表团聚体，用0代表团聚体间的孔隙。图2列出了经数字化后的原状土和扰动土的三维图像。每个图像由200×200×200像素组成。Quin等[18]详细介绍了土壤三维图像的获取过程。在图2中，土壤1是扰动土的图像，土壤2为原状土的图像。为了对比，研究了一个是由圆形团聚体构成的理想土壤（土壤3）。在所有土壤中，由于团聚体内的孔隙相对较小、在30 μm分辨率下不能识别，因此，图2中的固相为土壤团聚体，气相为团聚体间的孔隙，溶质在团聚体内可以通过分子扩散形式运移。
图1 二维团聚体土壤切片
（图中黑色代表孔隙，灰色代表土壤团聚体）
图2 3种土壤的数字化三维图像
式（3）中的记忆函数描述了溶质从土壤团聚体间的空隙（图1黑色区域）向团聚体内（图1灰色区域）的平均迁移速率，是时间的函数。其物理意义是t=0时从团聚体表面进入团聚体内的一个化学分子在t时刻仍滞留在团聚体内的概率。因此，该交换速率与土壤团聚体的几何形状和扩散溶质的能力有关，但与团聚体间孔隙（即图1中黑色区域）的传递能力以及溶质质量浓度无关。
为便于计算溶质交换速率，假定土壤中的初始溶质质量浓度为0。在t=0时刻，土壤团聚体之间的溶质质量浓度从0升至C0，然后保持不变，而团聚体内的溶质质量浓度在t=0时刻依然为0。另外假定团聚体检的水流速度为0。在这些条件下，团聚体间的溶质质量浓度变化为
是狄拉克函数。因为
是一个常数，式（1）和式（2）简化成如下的公式：
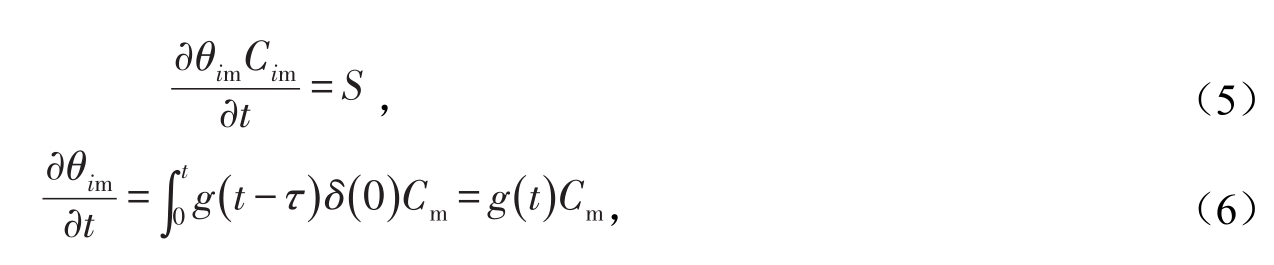
式（6）表明，在上述设定的条件下，团聚体土壤的记忆函数等于团聚体内部溶质质量浓度随时间的变化。因此，通过模拟溶质从团聚体之间（图1地黑色区域）向团聚体内（图1的灰色区域）的扩散运动，可以直接计算记忆函数。
对图2（a）—图2（c）所列的3个土壤，利用孔隙尺度模型模拟了溶质从团聚体间向团聚体内的扩散运动。在上述特定条件下，溶质从团聚体间向团聚体内的运动可用如下的三维分子扩散方程描述[19]：
式中：c为土壤团聚体内部溶质的质量浓度(mg/L)；Γ为土壤团聚体的外表面（即图1中黑色和灰色的界面，图2中红色与黄色之间的界面）。利用有限体积法求解式（7）。在模拟过程中，将三维图像的像素（即30× 30×30µm3的正方体）直接用作有限体积法的积分单元。利用不同时刻模拟的溶质在团聚体内的三维质量浓度分布，每一土壤的记忆函数可通过下述的公式计算：
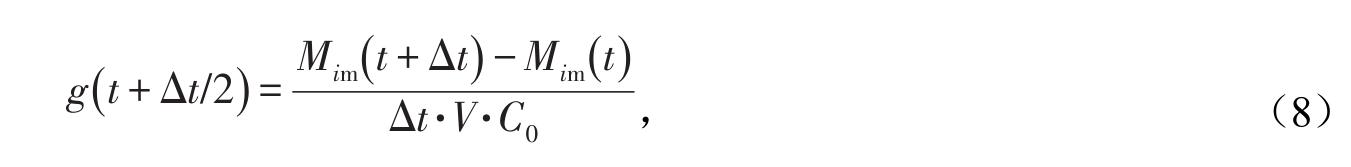
式中：Δt为时间步长(s-1)；V为土壤中团聚体的体积(cm3)。土壤团聚体内的溶质质量由下式计算：
式中：N为土壤团聚体单元的总数量；c(xi,t)为以xi为中心的单元体内的溶质质量浓度(mg/L)；ε为单元体的边长（30 μm）；De为土壤团聚体内的有效分子扩散系数(cm2/s)。
溶质在土壤团聚体内的有效分子扩散系数除与溶质本身的分子大小有关外，还与土壤温度和团聚体的内部结构有关。本文不专注研究某一特定的溶质，而是模拟不同有效分子扩散系数对记忆函数的影响，并分析能否利用从一种溶质计算获得的记忆函数来估算其他溶质的记忆函数。对于给定的溶质，其在团聚体内的有效扩散系数与其在自由水中的分子扩散系数成正比，其比值为土壤团聚体的弯曲度。图2中左边的三图为用图像技术获取3种土壤的三维图像（黑色代表孔隙，黄色是土壤团聚体）。右边的图为土壤团聚体内的有效扩散系数为De=0.089D0时，溶质质量浓度在9 s时在团聚体内的分布，图中的质量浓度光谱从红色（mg/L）到蓝色（0.004 mg/L）
为便于分析，以下用硝态氮在18oC水中的分子扩散系数（D0）和三维图像，每一个像素的边长（δ= 30µm）对时间t进行无量纲化处理，即
利用像素的边长，对空间进行了无量纲化处理。另外，用硝酸盐在18℃水中的分子扩散系数
为参考值，对团聚体内的有效分子扩散系数进行无量纲化处理。
兹对溶质在图2所列3种土壤团聚体内的运移过程进行了数值模拟。为了直观了解团聚体结构对溶质运移的影响，图2（d）—图2（f）给出了在同一时刻同一溶质在3种土壤中的质量浓度分布情况。利用图2所示的三维质量浓度分布，利用式（8）直接计算出了不同溶质在每一种土壤内记忆函数随时间的变化，3种土壤的记忆函数类似。兹以土壤1为例，详细介绍模拟结果。溶质在水中的分子扩散系数与其分子质量有关，利用不同的分子扩散系数代表不同的溶质，并对其进行了模拟计算。不同溶质在团聚体内的平均有效分子扩散系数从De=0.253D0（氢离子）减小到De=0.052D0（溶解的碳水化合物）。图3分别给出了在常规坐标和单对数坐标系下（图3中的小图）不同溶质记忆函数随时间的变化情况。从图3可以看出，在单对数坐标系下记忆函数并非随时间线性衰减，亦即，指数分布函数不能准确描述记忆函数随时间的变化过程。特别是在初期，记忆函数随时间的衰减速度要远比指数函数描述的快。以上分析表明，常用的可动-不可动水体模型仅仅是拟合模型和试验结果，并不能准确地描述团聚体内外的溶质交换过程。亦即，溶质在团聚土壤内可动与不可动水体之间的溶质交换并非与其在2个水体内的质量浓度差成正比。
图3 记忆函数拟合值与模拟结果对比
为了正确描述溶质在团聚土壤中的运动和转换过程，可以直接利用图3中的质量交换速率与式（4）结合来模拟溶质的运移过程，但这种方法需要数值积分，计算工作量比较大、实际应用不太方便。为便于运用，提出了一个简单的分析公式来近似计算图3的结果。文献中有不同的经验公式来描述记忆函数，但这些公式都不能准确地描述图3的计算结果。作为改进，提出如下的广义伽玛分布函数。广义伽玛分布函数没有解析表达式，其通过如下的拉普拉斯变换定义的[20]：
式中：α,β和k均为常数。当β=1，式（10）变为常规的伽玛分布函数；当β=k=1时，式（10）变为指数分布函数；α的单位与时间相同，参数β和k是无量纲的。因此，对于给定的土壤，β和k应该是相同的，而α的大小取决于溶质在团聚体内的扩散能力，即溶质的分子扩散系数。
将从
计算的所有记忆函数用式（10）拟合，然后将拟合值和孔隙的模拟结果进行对比，对比结果和参数值见图3。图3的对比结果表明，①当溶质在团聚体内的有效分子扩散系数较小时，式（10）能准确描述记忆函数早期随时间的衰减；②当溶质在土壤团聚体内的有效分子扩散系数较大时，式（10）不能精确描述记忆函数在晚期随时间的衰减。但总体来说，与指数分布函数相比，式（10）能很好地描述模拟记忆函数随时间的变化。
式(10)中的参数β为无量纲参数，对同一土壤应为常数，与溶质本身的分子扩散系数无关。而参数α的量纲与时间相同，其值随土壤团聚体的有效分子扩散系数D'=De/D0的改变而变化。对于图2所列的土壤1，α随D'按照α=0.0214D'线性增加。为了进一步证明这种线性关系是否适应于其他土壤，对图2中的其他2种土壤进行了分析，结果见图4。对于这3种土壤，α以不同的速率随土壤团聚体的有效分子扩散系数线性增加，但增加的速率随土壤而异。对同一种土壤，若其与溶质A所对应的参数α是αA，则其对溶质B对应的参数αB可用如下公式描述：
式中：DA和DB分别为溶质A和溶质B在纯水中的分子扩散系数。
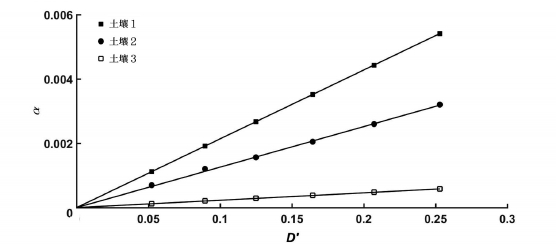
图4 参数α随有效分子扩散系数变化趋势
式（10）虽然能准确地描述团聚体内外的溶质交换速率，但没有时间域的解析表达式。在实际应用时要将溶质运移式（4）进行拉普拉斯变换方可应用，这需要水流速度处于稳定状态、弥散系数不随时间变化，实际应用有一定的局限性。若流速随空间变化，拉普拉斯变换后的方程无解析解，需要用数值反演计算质量浓度分布，计算相当复杂。一种改进的方法是多区模型[16]，多区模型将团聚体分成几个区域，每一个区域内的溶质可直接与团聚外的溶质交换，其交换速率与该区域和团聚体外的质量浓度差成正比。但多区模型需要很多参数，这些参数要通过拟合的方法确定。因本文的目的是介绍如何用图像技术和数值模拟计算团聚体内外的交换速率，并对常用的模型进行评估，本文不再对其他模型深入讨论。
利用X-射线成像技术对质地不同土壤在30µm的精度下进行了扫描，获得了土壤团聚体和团聚体间孔隙结构的三维图像，然后利用孔隙尺度模型对不同溶质从团聚体外向团聚体内的分子扩散进行了数值模拟，并利用模拟结果详细计算了团聚体内和团聚体外之间溶质的交换速率，亦即俗称的记忆函数或二区模型。计算结果表明，目前常用的基于Coats and Smith[13]提出的可动-不可动水体模型不能准确地描述溶质在这2个水体之间的交换、2个水体之间的溶质交换速率并非与二水体间的质量浓度差成正比。另外，常用的伽玛分布函数也有很大误差。虽然这2种模型是描述团聚土壤内溶质运移的常用模型，并能较好地拟合试验结果，但这种拟合是靠调整所有的参数来实现的，而并非真正描述了土壤团聚体内外的溶质交换过程。为此，本文提出了一个广义的伽玛分布函数，能更好地描述团聚内外溶质的交换过程。
自然界的土壤非常复杂，溶质在其孔隙中的运移与转化受多种因素影响和控制。在数值模拟中，每一个过程通常用几个参数或公式来描述。由于不同的参数组合可能会给出相同的质量浓度时空分布，单纯通过模型和试验数据对比很难判断这些参数和公式是否正确地描述了土壤中的每一个物理过程。三维图像技术和数学模型的发展为研究土壤中溶质运移的每一个详细过程提供了新的途径，本文首次利用该技术对土壤团聚体内外的溶质交换进行了研究。
参考文献：
[1]孙玉龙,郝振纯.TDR技术及其在土壤水分及土壤溶质测定方面的应用[J].灌溉排水学报,2000,19(1):39-40.
[2]SIMUNEK J,JARVIS N J,VAN GENUCHTEN M T,et al.Review and comparison of models for describing non-equilibrium and preferential flow and transport in the vadose zone[J].Journal of Hydrology,2003,272:14-35.
[3]王全九.土壤溶质迁移理论研究进展[J].灌溉排水学报,2005,24(3):77-79.
[4]余根坚,黄介生,高占义.基于HYDRUS模型不同灌水模式下土壤水盐运移模拟[J].水利学报,2013,44(7):829-830.
[5]刘春卿,杨劲松,陈小兵，等.石河子垦区灌耕灰漠土饱和-非饱和土壤水动力弥散试验研究[J].灌溉排水学报,2008,27(1):39-40.
[6]BLUNT M J,BIJELJIC B,DONG H,et al.Pore-scale imaging and modelling[J].Advavances in Water Resources，2013,51:197-216.
[7]ZHANG X X,CRAWFORD J W,YOUNG I M.Does pore water velocity affect the reaction rates of adsorptive solute transport in soils Demon stration with pore-scale modelling[J].Advances in Water Resources.2008,31:425-437.
[8]FATT I.The network model of porous media:1.Capillary pressure characteristics.Transactions of the American Institute of Mining and Metal lurgical Engineers[J].1956,207:144-159.
[9]REEVES P C,CELIIA M A.A functional relationship between capillary pressure,saturation,and interfacial area as revealed by a pore-scale network model[J].Water Resources Research，1996,32:2 345-2 358.
[10]ZHANG X X,CRAWFORD J W,FLAVEL R J,et al.A multi-scale Lattice Boltzmann model for simulating solute transport in 3D X-ray mi cro-tomography images of aggregated porous materials[J].Journal of Hydrology,2016,541:1 020-1029.
[11]MOONEY SJ,PRIDMORE TP,HELLIWELL J,et al.Developing X-ray Computed Tomography to non-invasively image 3-D root systems ar chitecture in soil[J].Plant and Soil,2012,352:1-22.
[12]张英虎,牛健植,汪西林，等.土壤溶质优先迁移影响因素研究进展[J].灌溉排水学报,2013,32(3):34-36.
[13]COATS K H,SMITH B D.Dead-end pore volume and dispersion in porous media[J].Society of Petroleum Engineers Journal，1964（4）:73-84.
[14]HAGGERTY R,MCKENNA S A,MEIGS L C.On the late-time behavior of tracer test breakthrough curves[J].Water Resources Research, 2000,36:3 467-3 479.
[15]CHEN W,WAGNET R J.Description of atrazine transport in soil with heterogeneous nonequilibrium sorption[J].Soil Science Society of America Journal,1997,61:360-371.
[16]HARVEY D,PHAROAH J G,KARAN K.A comparison of different approaches to modelling the PEMFC catalyst layer[J].Journal of Power Sources,2008,179:209-219.
[17]PANG L P,CLOSE M,SCHNEIDER D,et al.Effect of pore-water velocity on chemical nonequilibrium transport of Cd Zn and Pb in alluvial gravel columns[J].Journal of Contaminant Hydrology,2002,57:241-258.
[18]QUIN P R,COWIE A L,FLAVEL R J,et al.Oil mallee biochar improves soil structural properties-A study with x-ray micro-CT[J]. Agriculture Ecosystems&Environment,2014,191:142-149.
[19]HU W L,HUANG N,ZHANG X X.Impact of saturation on mass transfer rate between mobile and immobile waters in solute transport within aggregated soils[J].Journal of Hydrology,2014,519:3 557-3 565.
[20]CVETKOVIC V.Ageneral memory function for modeling mass transfer in groundwater transport[J].Water Resources Research,2012,48:12.
Calculating Mass Transfer Between Waters inside and between Aggregates in Aggregated Soils Using Tomography and Pore-scale Modelling
CHEN Xuejun1，JIANG Baoliang2，ZHANG Xiaocai2
（1.Jiyuan Vocational and Technical College,Jiyuan 454650,China; 2.North China University of Water Resources and Electric Power,Zhenzhou 450016,China）
Abstract：Most natural soils are aggregated due to the impact of soil organic matters and soil micro organisms.In aggregated soil,mass transfer between waters inside and between its aggregates is an important process for soil to retain and supply water and nutrients,but is difficult to measure experimentally.Therefore,in chemical transport modelling such mass transfer is often described using an empirical memory function with its parameters obtained by calibrating against experimental data.In practical applications,however,it is impossible to judge that a calibrated memory function correctly describes the processes occurring in soil or it is just a bridge to link model and measurements.Instead of using empirical memory function,we propose in this paper to directly calculate it using soil image and pore-scale modelling.Images of three soils are acquired using x-ray computed tomography at resolution of 30µm with the between aggregates pores and aggregate geometries explicitly resolved.The mass transfer between solute inside and between the aggregates is calculated using a pore-scale modeling for difference solutes.The results showed that the commonly used exponential memory function associated with the mobile-immobile water model is unable to describe the mass exchange in all three soils.As an improvement,we propose and prove a generalized gamma distribution to describe the mass exchange processes.
Key words:mass transfer;X-ray micro-tomography;aggregated soils;pore-scale modelling;mobile-immobile water model
中图分类号：S271；S278；S273.4
文献标志码：A
doi：10.13522/j.cnki.ggps.2017.08.007
责任编辑：赵宇龙
陈学军，姜宝良，张晓偲.基于三维图像技术和数学模型的土壤团聚体内外溶质交换速率研究[J].灌溉排水学报，2017，36（8）：39-45，52.
收稿日期：2017-02-21
作者简介：陈学军（1961-），男，河南平舆人。高级工程师，主要从事国土资源管理研究。E-mail：cx_xiao0913@163.com
通信作者：姜宝良（1962-），男，河南宜阳人。教授级高级工程师，主要从事地下水和水工环教学研究工作。E-mail：13703849008@163.com
文章编号：1672-3317（2017）08-0039-08