0 引言
近年来,随着国家“节水增粮”行动的开展,滴灌灌溉技术在东北地区得到快速发展[1-2],2011—2015年辽宁共发展40万hm2,其中,辽宁西部的绝大部分地区采用滴灌技术[3]。滴灌技术在区域水资源高效利用和保障粮食安全等方面均起到明显的效果;但在应用过程中,也出现了一些由于设计不合理,导致工程投入增加等问题,降低了工程效益。支管轮灌小区是以一条支管控制面积的灌溉范围为基本灌水单元[4],一个或多个支管轮灌小区构成一个轮灌组。在水源供应允许的条件下,支管轮灌小区可通过扩大灌水小区面积和对不同灌水小区面积块进行优化组合来降低整个灌溉系统的建设费用,该部分的规划设计是否合理,将直接影响到系统的工程投资、运行费用和安全可靠性。因此,对灌水小区管网进行优化设计,在满足系统流量、灌水均匀度及可靠性要求的条件下,寻求灌水小区优化设计方案,具有十分重要的现实意义。
国内外学者对田间灌溉小区管网优化问题进行了一些研究。研究指出,将田间管网允许水头差按0.45、0.55分配给支管和毛管是比较经济的[5];以支毛管管材最省为目标建立模型,得到田间管网允许水头差的分配比例计算公式[6];建立田间管网优化模型,可以求解使管网投资最低的支管、毛管管径[7];建立坡地田间管网优化模型,通过支管变径,使田间管网的灌水均匀度最大[8];提出了一种优化方法,计算毛管上每个灌水器的压力、流量及特征值,使灌水器平均流量等于灌水器设计流量,优化支管和毛管管径[9];依据最佳支管位置的定义,采用能量廓线法推导出了确定最佳支管位置的一种简易计算方法,并提出了满足允许的最大压力水头和最小压力水头的微灌系统双向毛管设计方法[10];以二侧毛管灌水器平均工作压力相等为基础,导出微灌双向异径毛管最佳支管位置、进口工作压力、水力流量偏差系数以及极限管长的计算公式,同时给出了最佳支管位置参数[11];在不限定管网系统面积的情况下建立了田间管网及骨干管网的优化设计数学模型,可同时完成相应管网的优化布置和优化设计且能得到最佳控制面积[12]。目前,关于田间管网的优化已有一定研究,但主要集中于管网允许压力差在支管、毛管的分配比上,并没有将支管、毛管作为一个整体进行水力解析和优化设计。为此,将支管、毛管作为一个整体,通过建立数学模型,对管网布置进行优化,利用遗传算法对模型进行求解,得出滴灌支管轮灌小区管网布置优化方案。
1 材料与方法
田间管网由若干段毛管和若干段支管连接而成。毛管的管段长度由灌水器间距决定,支管的管段长度根据作物种植特征确定。各种管径支管、毛管的总长度为管段长度与段数的乘积,将各种管径的支管和毛管段数作为优化变量X、Y。灌水小区管网连接形式如图1所示。

图1 支管轮灌小区管网连接示意图
1.1 目标函数
分别以单位面积投入费用最低和小区控制面积最大为目标,选择辽西地区常用的滴灌田间管网常用管材中不同管径的支管和1种毛管,依据优化模型可以得到支管和毛管的管段数,进而确定灌水小区管网投资和控制面积。
灌水小区单位面积管网最低费用和最大控制面积模型可表达为:
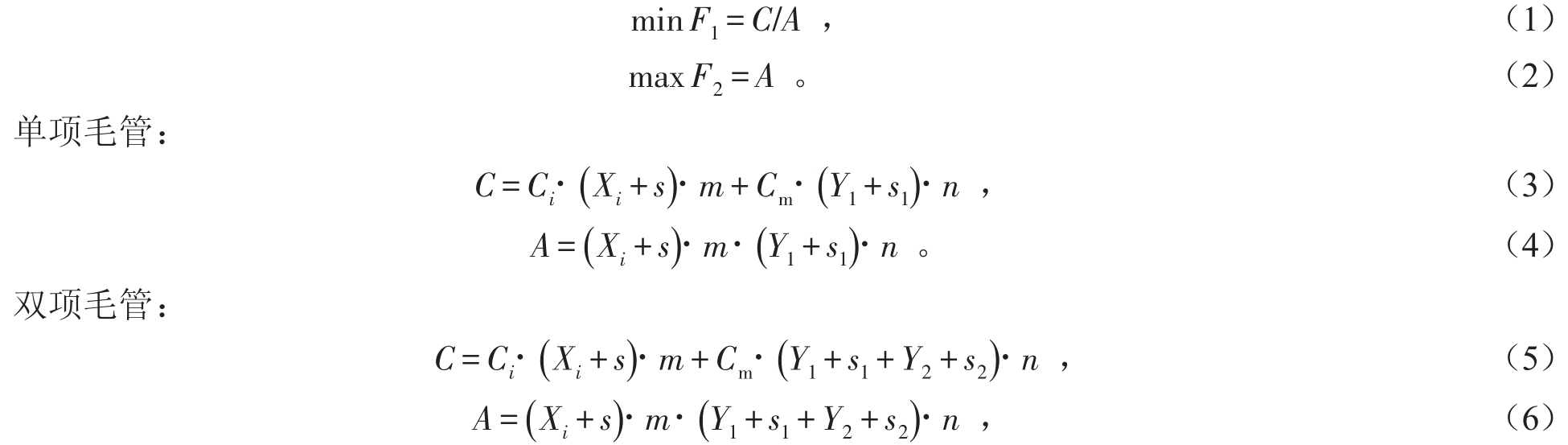
式中:F1为单位面积最低费用(元/hm2);F2为最大控制面积(hm2);C为灌水小区网管投资费用(元);A为灌水小区灌溉控制面积(hm2);Ci为第i种支管的单位价格(元/m);s为支管首端余量比(支管入口到第一个毛管的长度与相邻2个毛管距离的比值);Xi为第i种支管的管段数量;Cm为选用毛管的单位价格(元/m);Y1、Y2为毛管管段数;s1、s2为毛管首端余量比(毛管入口到第一个灌水器长度与相邻2个灌水器距离的比值);m为相邻2条毛管的间距(m);n为相邻2个灌水器的间距(m)。
1.2 约束条件
根据微灌工程技术规范[13],微灌系统灌水小区灌水器设计允许流量偏差应满足:
灌水器水头偏差率和流量偏差率计算式为:

式中:hmin为灌水器最小工作水头(m);hmax为灌水器最大工作水头(m);hd为灌水器设计工作水头(m);hv为灌水器水头偏差率(%);qv为灌水器流量偏差率(%);x为灌水器流态指数。
假定灌水小区各灌水器流量均为设计流量,以整个灌水小区系统内各灌水器最大压差值应控制在允许压力差范围内作为约束条件,使整个小区满足流量偏差要求。
管网各节点压力水头计算式为:

式中:Hk为k孔压力水头(m);H0为入口压力水头(m);Li为从入口处算起的各出口间管段长度(m);Ii为地面坡度(m/m);Ji为水力坡度(m/m);k为灌水器编号;P为多孔管孔口数;a为局部水头损失加大系数;f、m、b为水头损失计算系数;Q为灌水器流量(L/h);dj为管路内径(mm)。
局部水头损失加大系数,一般取值为1.05~1.30,兹取1.1。常见管材f、m、b取值见表1。
表1 各种管材的摩阻系数、流量指数和管径指数

1.3 模型求解方法
遗传算法的基本思想是对自然界生物遗传和变异的数学抽象,非常适用于复杂系统,可以进行全局优化的随机搜索方法,其求解过程是通过数学编码模拟染色体上基因之间的选择、交叉和变异的进化过程来完成的,通过随机生成的初始解,经过不断进化,最终得到满足条件的优化解。兹采用遗传算法工具箱对模型进行求解,遗传算法工具箱的使用参考文献[14]。具体求解步骤为:
①编码:遗传的变量为支管管径、管段数和毛管灌水器数量,支管管段数与毛管灌水器数量都为整数,故采用整数编码,将支管管径按其管径进行编号,形成一个有序的整数数列。
②适应度函数:将目标函数作为适应度函数,为满足遗传算法对适应度函数最大化的要求,将目标函数的最小化问题转化为最大化问题,对于不满足约束条件的个体,引入惩罚函数将其适应度值取为0。
③遗传操作:采用MATLAB遗传算法工具箱中的函数来完成。采用sus函数,个体适应度值代表被选择的概率,在概率控制下找出最优个体;由于所有基因位均采用整数编码,故交叉操作采用xovsp函数,在交叉概率Pc控制下,将所选择的父个体随机配对;变异操作采用mut函数,在变异概率Pm控制下,随机选择需要变异的个体。
2 结果与分析
2.1 应用
辽宁西部地区某灌区所选用的灌水器设计流量为1.38 L/h,支管管径取表2中全部管径种类,毛管管径取16 mm,支管出水口间距为1 m,支管入口到第一个毛管的距离为0.5 m,毛管灌水器间距均为0.3 m,毛管入口至第1个灌水器的距离为0.15 m,局部水头损失加大系数取1.1。
表2 待选管径及单价

2.2 结果分析
将有关数据代入到模型中进行优化计算,遗传算法采用MATLAB R2012a遗传算法工具箱实现,参数设置:初始种群Z=50,交叉概率Pc=0.9,变异概率Pm=0.05,进化代数为100,得出管网优化布置方案,结果见表3。
2.2.1 毛管布置方式对优化结果的影响
由表3可知,单位面积投资最低模型下,单向毛管灌水小区管网最低投资为2 869.61元/hm2,控制面积为0.121 7 hm2,支管管径为32 mm,支管长度为10.5 m,毛管长度为115.95 m。双向毛管灌水小区管网最低投资为2 746.01元/hm2,控制面积为0.172 0 hm2,支管管径为32 mm,支管长度为8.5 m,毛管长度为101.25 m。与单向毛管相比,双向毛管单位面积投资降低了4.31%,说明双向毛管布置更有利于降低灌水小区单位面积管网投资。
表3 单位面积投资最低管网优化布置结果

由表4可知,控制面积最大模型下,单向毛管灌水小区管网最大控制面积为0.698 7 hm2,投资为4 265.73元/hm2,支管管径为75 mm,支管长度为77.5 m,毛管长度为90.15 m。双向毛管灌水小区管网最大控制面积为0.897 2 hm2,投资为3 436.49元/hm2,支管管径为75 mm,支管长度为54.5 m,毛管长度为82.35 m。与单向相比,双向毛管最大控制面积增加了28.41%,单位面积投资减少了19.44%,说明双向毛管布置更有利于增加灌水小区控制面积。
表4 控制面积最大管网优化布置结果

2.2.2 支管管径对优化结果的影响
以双向毛管为例(见表5),在单位面积投资最低模型下,当支管管径由75 mm减小到32 mm时,最低投资由3 102.91元/hm2降低到2 746.01元/hm2,降低了11.50%;控制面积最大模型下,当支管管径由32 mm增大到75 mm时,最大控制面积由0.181 7 hm2增加到0.897 2 hm2,控制面积增加了393.78%。说明减小支管管径有利于降低单位面积投资,增大支管管径有利于增加灌水小区控制面积。
表5 不同支管管径下双向毛管单位面积最低投资和最大控制面积

3 结论与讨论
1)将支管和毛管作为一个整体,以田间管网单位面积费用最低和控制面积最大为目标函数,在不限定田间管网规模及布置形式的情况下,建立了单向毛管及双向毛管田间管网优化设计数学模型,并采用遗传算法进行求解,能够得到管网优化布置方案。
2)结合实例,在最小投资模型下,双向毛管单位面积投资较单向毛管降低了4.31%;在最大控制面积模型下,双向毛管最大控制面积较单向毛管增加了28.41%,说明双向毛管灌溉小区管网布置方案在控制面积及投资二方面均优于单向毛管,这与已有研究结果[12]相同,其原因为支管管径相同时,滴灌小区单位面积投资和控制面积取决于支管和毛管长度,双向毛管布置减少了支管长度,增加了毛管长度,有利于减少单位面积投资和增加控制面积,在滴灌小区管网设计中应优先考虑双向毛管布置方案。在水源供应允许的条件下,当支管管径由32 mm增大到75 mm时,控制面积增加了393.78%,说明增大支管管径有利于增加滴灌小区控制面积,这与相关研究结果[15]一致,这是由于支管管径的增加改善了灌水小区的水力性能,降低了滴灌小区的水头偏差率;当支管管径由75 mm减小到32 mm时,单位面积投资降低了11.50%,说明减小支管管径有利于降低单位面积投资,这与通过工程实践得到的结论[16]相似,这是由于管径减小大幅降低了管材费用,从而降低了投资,但支管管径减小滴灌小区面积会随之减小,若滴灌系统首部控制面积不变,则会增加灌水小区数量,从而增加灌水管理成本[17]。因此,滴灌小区管网设计中应综合考虑单位面积投资和管理成本选择合适的支管管径。支管轮灌小区只是滴灌大系统的组成部分,支管轮灌小区面积和组合方式对大系统单位面积投资及管理成本影响很大。因此,考虑灌水管理成本的滴灌大系统的管网优化模型仍需进一步研究。
参考文献:
[1]窦超银,孟维忠.膜下滴灌在辽西半干旱区不同地形条件下的应用研究[J].节水灌溉,2014(8):19-21.
[2]窦超银,孟维忠.控制灌溉在玉米大垄双行膜下滴灌种植中的应用研究[J].东北农业科学,2014,39(1):16-19.
[3]陈伟,邵子玉,李亦韬,等.辽西北地区玉米适宜滴灌方式研究[J].灌溉排水学报,2016,35(5):38-42.
[4]杨光龙,洪亮.支管轮灌滴灌模式在大田应用中的优点浅述[J].农业科技与信息,2008(10):42.
[5]KEIIER J,KARMELI D.Trickle irrigation design parameters[J].Transactions of theASAE,1974,17(4):678-684.
[6]杨建康,陈学敏.微灌系统田间管网允许压力差的最优分配方法[J].水利学报,1990(7):31-36.
[7]白丹.微灌田间管网的混合整数规划模型[J].农业机械学报,1995,26(1):45-49.
[8]SAAD J C C,MARINO M A.Optimum Design of Microirrigation Systems in Sloping Lands[J].Journal of Irrigation and Drainage Engineering,2002,128(2):116-124.
[9]王新坤.微灌系统遗传算法优化设计理论与应用[M].北京:中国水利水电出版社,2010.
[10]蒋树芳,康跃虎,曲强.坡地上灌水器流量均等微灌双向毛管设计方法[J].农业机械学报,2011,42(7):82-85,129.
[11]鞠学良,吴普特,Paul W R,等.基于能坡线法的微灌双向异径毛管设计[J].农业机械学报,2015,46(12):47-54.
[12]李援农,马朋辉,胡亚瑾,等.灌区自压微灌独立管网系统优化设计研究[J].水利学报,2016,47(11):1 371-1 379.
[13]GB/T 50485—2009,微灌工程技术规范[S].
[14]雷英杰,张善文.MATLAB遗传算法工具箱及其应用[M].第二版.西安:西安电子科技大学出版社,2014.
[15]李援农,朱锋.基于最大控制面积和最低费用的微灌小区管网优化[J].农业工程学报,2015,31(23):80-87.
[16]窦超银,孟维忠.滴灌支管轮灌模式中管网布置形式的改进研究[J].节水灌溉,2015(6):95-97.
[17]张志新.滴灌工程规划设计原理与应用[M].北京:中国水利水电出版社,2007.
 X1 X2 X3 X4支管
X1 X2 X3 X4支管 75 63 50 32 66.4 55.8 44.2 27.4 16.68 11.75 7.23 4.12
75 63 50 32 66.4 55.8 44.2 27.4 16.68 11.75 7.23 4.12