0 引言
土壤水分特征曲线是土壤水吸力与土壤含水率的关系曲线,表示土壤水的能量和数量之间的关系[1],是农田土壤水分运动重要的水力学参数,同时对于土壤持水性和水分有效性评价具有重要作用[2-3]。目前较多采用离心机法对土壤水分特征曲线进行测定,而在脱水过程中较强的离心力导致土壤体积质量发生变化,这与田间土壤发生湿胀干缩一致[4-5],因此在对土壤水分运动特性进行研究时,应对土壤体积质量的变化加以考虑,以真实地反映土壤水运动过程和土壤收缩特征。目前虽然已有关于土壤体积质量变化对土壤水分特征曲线影响的研究[6-7],但较多研究是以不同初始体积质量作为试验处理,而关于土壤水分特征曲线测定过程(即脱水过程)中土壤体积质量变化对其影响的研究鲜有报道。由于目前尚较难从机理角度全面描述土壤水分特征曲线,所以关于土壤水分特征曲线的研究仍停留在模型的拟合上[8-9]。然而,土壤水分特征曲线仅定量描述了土壤含水率与吸力之间的关系,并未反映出在脱水过程中的土壤收缩特性,故仅依赖于土壤水分特征曲线不便于对土壤收缩特性展开研究。因此,将土壤收缩曲线与土壤水分特征曲线相结合,有利于定量分析土壤体积质量、含水率和吸力的关系。另一方面,土壤因干旱所致的收缩将产生裂缝,不但破坏作物根系,而且易导致土壤水分和养分流失,从而抑制作物吸收养分,最终导致产量降低[10]。因此,开展土壤收缩特征曲线(即土壤质量含水率与比容积的关系)方面的研究,对于揭示土体稳定性、压缩性和渗透性等的变化规律具有重要科学意义。
综上,田间土壤结构易被破坏,可导致体积质量不均匀且发生变化,因此在研究土壤持水特征和收缩特征时,充分考虑土壤体积质量的变化更具有实际意义[11],同时有利于为其他土壤物理特性的研究奠定基础。基于此,以辽宁砂壤土、云南黏壤土、陕西黏壤土和山东壤土作为供试土壤,分别对土壤持水特征和土壤收缩特征进行研究,定量分析脱水过程中土壤体积质量、含水率、吸力的关系,并进一步通过土壤收缩特征值将土壤收缩曲线划分为3个典型直线型收缩段,以期为土壤水力参数估算和变体积质量土壤水分运动模拟提供一定科学依据。
1 材料与方法
表1 供试土壤颗粒组成
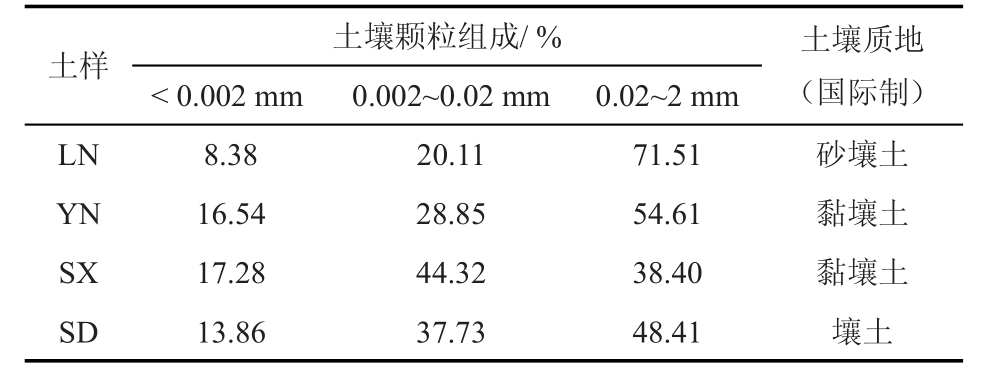
供试土壤分别取自辽宁(LN)、云南(YN)、陕西(SX)和山东(SD)地区0~30 cm耕作层,其分别位于我国的东北、西南、西北和华东地区,该取样拉开了土壤采集的尺度,可在一定程度上保证研究成果的普适性,同时避免了同一地区取样,土壤特性参数相差不大的缺陷。当然,对于不同土壤质地脱水过程土壤体积质量、含水率、吸力的关系,用于分析的土样越多,其结果的代表性越强,但考虑到更大范围采集土样的困难等实际情况,故选取该4个区域具有代表性的土壤质地进行分析。土样经风干、过2 mm筛后,采用激光粒度仪(Mastersizer 2000)测定土壤颗粒组成(表1)。按田间土壤体积质量将供试土壤均匀装入与离心机配套的环刀内,以便于集中管理进行脱水。试验中,根据实测土壤体积质量,将LN、YN、SX和SD土样的装填体积质量分别设定为1.2、1.3、1.4和1.6 g/cm3(各样品均4次重复)。试验开始前将全部环刀样品置于蒸馏水中饱和处理48 h,而后将饱和处理后的环刀样品置于高速恒温冷冻离心机(CR21GⅡ型)内测定土壤水分特征曲线,基于RETC软件,采用应用广泛且结构简单的Brooks-Corey(BC)模型对实测值进行拟合,以获取土壤水分特征曲线。土壤脱水过程中,离心机内恒温4℃,吸力范围为0~7000 cm,每阶段离心结束时用电子天平(精度为0.01 g)称量样本质量,同时采用游标卡尺测定土面到环刀口的距离(即土体沉降高度)以计算土壤收缩度,进而确定离心过程中各吸力所对应的土壤体积质量。试验结束后置于105℃恒温箱内干燥24 h,以计算土壤质量含水率,结合各吸力对应的土壤干体积质量将其转化为体积含水率。
2 结果与分析
2.1 含水率与吸力的关系
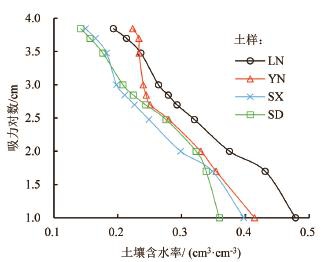
图1 土壤水分特征曲线
通常采用土壤水分特征曲线对土壤含水率(θ)和吸力(h)的关系进行描述,为更直观、清晰地表示土壤含水率随吸力的变化,土壤水分特征曲线采用半对数坐标图,即将吸力取对数(log10(h)),如图1所示。
由图1可知,4种土壤水分特征曲线形态类似,且均表现出含水率随吸力增大而减小的趋势,但在脱水过程中,土壤含水率的减小速率存在差异,即当土壤含水率接近饱和含水率和土壤较干时,减小速率较小;而介于二者之间时,减小速率较大。在测定土壤水分特征曲线过程中,当吸力从0增加至7000 cm时,土壤含水率整体呈现减小趋势,而其减小速率则整体呈现出“慢—快—慢”的变化趋势,其中以YN土样最为明显。
采用RETC软件对其进行拟合发现,BC模型可以很好地表征4种供试土壤的含水率和吸力之间的关系,其决定系数R2均大于0.99(拟合参数列于表2);另一方面,土壤含水率(θ)与吸力(h)的关系还可以通过比水容量C(h)表示,即C(h)=dθ/dh。研究中4种不同地区的供试土壤持水能力、土壤含水率随吸力增加而递减的速率均存在差异,这可能是由于供试土壤质地和装填土时的压实度存在差异等原因所致。
表2 土壤水分特征曲线拟合参数

2.2 土壤体积质量与吸力的关系
采用离心机法测定土壤水分特征曲线时,土壤干体积质量随着吸力增加而呈现逐渐增加趋势,但增加幅度逐渐减小(表3)。分析认为,当吸力较低时,土壤内大孔隙较多,排水效果明显,故土壤体积质量增加幅度较大;随着吸力增加,土壤中大孔隙数量逐渐减少,排水效果相对不明显,故土壤体积质量增加幅度较小。
表3 脱水过程中土壤干体积质量

为定量分析土壤体积质量与吸力的关系,将脱水过程中的干体积质量变化视为土壤轴向收缩,将其与BC模型结合即可获取土壤体积质量与吸力的关系。对BC模型进行简化,即:
式中:r为拟合参数;其他符号意义同前。由于土壤脱水过程中,在正常收缩段内土壤水分的减少量与土壤容积的减少量相等,同时参照文献[12-13],对于土壤三直线收缩模型,其正常段斜率接近于1,故土壤收缩模型可描述为:
式中:v为比容积(cm3/g);γ为干体积质量(g/cm3);θm为质量含水率(g/g);k为经验常数,从理论上,k为含水率为0时的比容积(k=1/γs)。结合式(1)和式(2),可得土壤体积质量与吸力之间的定量关系[13],即:
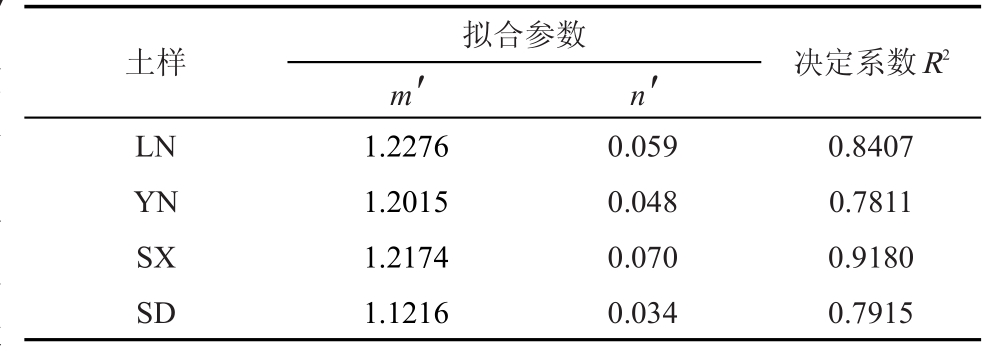
式中:γs为土壤密度(g/cm3),农田耕层土壤密度一般可取2.65 g/cm3;γsat为土壤饱和时的体积质量(g/cm3);m′和n′分别为拟合参数。采用式(3)对4种土壤体积质量和土壤吸力的关系进行拟合,结果见表4。由表4可看出,土壤体积质量与吸力符合较好的幂函数关系,满足精度要求,故在土壤脱水过程中,将土壤收缩特性与水分特征曲线模型(BC模型)相结合,可定量分析土壤体积质量和吸力的关系。
表4 供试土壤体积质量与吸力的关系
2.3 含水率与体积质量的关系
在脱水过程中,随着离心机转速和吸力的增加,土壤含水率显著降低,土壤发生收缩变化,然而土壤容积的变化可以通过其变化速率描述,故土壤含水率和体积质量之间的关系可以通过土壤收缩特征曲线表示,即比容积(土壤体积质量的倒数)-含水率曲线,结果见图2。
从图2可以看出,4种供试土壤的收缩特征曲线均基本呈现“S”型,随着土壤含水率的增加,比容积呈现递增趋势(土壤体积质量呈现递减趋势),但在不同阶段其增加速率不同,故可采用三直线模型分别对3个阶段进行拟合[14-15]。研究中,土壤收缩特性明显受离心力影响,可将土壤收缩的3个阶段划分为超正常段、结构段和伪饱和段;在不同的收缩阶段,土壤收缩特征值通常亦不相同。
土壤收缩特征值(p)即为比容积-含水率曲线上任意一点的斜率,可用来判断土壤容积变化与水容积变化的比例[16]。在正常段中,p≈1;在外力作用下,即在超正常段中,p>1,表示土壤容积随含水率的变化发生显著变化;结构段与正常段/超正常段相连接,p<1;当土壤含水率接近饱和含水率时的土壤收缩段为伪饱和段,此阶段内比容积随含水率的变化趋于平缓。可见,超正常段、结构段和伪饱和段内的p呈逐渐减小趋势。基于上述划分准则,分别对4种供试土壤的收缩阶段进行划分,结果见表5。
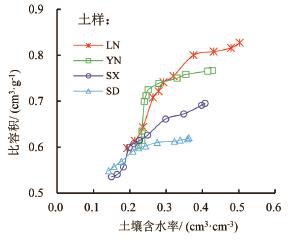
图2 土壤含水率与比容积的关系(土壤收缩特征曲线)
表5 供试土壤不同收缩段内土壤含水率与土壤体积质量的关系

由表5可知,4种土壤的收缩变化均可大致划分为超正常段、结构段和伪饱和段等3个直线型(1/γ=p·θ+t,p和t为拟合参数)收缩段。根据各收缩段拐点处的物理意义可知,LN土样土壤进气点的含水率、极限膨胀点的含水率和饱和含水率分别约为0.264、0.375、0.502 cm3/cm3,YN土样的分别为0.251、0.354、0.427 cm3/cm3,SX土样的分别为0.198、0.299、0.407 cm3/cm3,由于SD土样无明显超正常段,故其极限膨胀点的含水率和饱和含水率分别为0.208、0.362 cm3/cm3。同时观察图2可知,各土壤的3个收缩段并无明显分界,为使得土壤水分收缩特征的拟合曲线更连续,进一步采用Logistic模型(1/γ=a/(1+e-b(θ-d))+c,a、b、c、d均为拟合参数)[17]进行拟合(表6),该模型可以较好地拟合土壤比容积与体积含水率之间的非线性关系以及表征土壤收缩特征曲线。
表64 种供试土壤Logistic模型参数拟合

3 讨论
土壤水分特征曲线是土壤物理学中的重要参数,通常采用烘干法获取土壤含水率(即质量含水率),并且需要通过土壤干体积质量将其转化为体积含水率,故正确认识土壤水分特征曲线测定过程中的土壤体积质量变化显得尤为重要。在众多土壤水分特征曲线测定方法中,离心机法以其操作简单、省时和可测吸力范围广等优点被广泛采用[5],在强离心力作用下,土壤样品发生收缩,且主要伴随轴向沉降,即土壤体积质量随吸力增加逐渐增大(表3),然而这一现象在较多研究中通常被忽略[18-19],即假设土壤体积质量恒定。该假设将导致土壤体积含水率被低估,进而降低土壤水力参数获取的准确性,在很大程度上不利于开展土壤水分运移模拟研究。鉴于此,在获取土壤体积含水率过程中综合考虑了土壤体积质量随吸力的变化,对土壤体积质量、含水率与吸力三者间的相互关系进行了研究,一方面有利于揭示土体压缩性和渗透性的变化规律,同时可为变体积质量土壤水分运动特性的模拟研究奠定基础,具有实际意义。
对于离心机法测定土壤水分特征曲线,本研究仅考虑了轴向收缩应变;然而研究[20]表明,土体径向收缩应变亦随土壤体积质量发生改变,故在未来研究中应进一步综合考虑轴向和径向收缩所致的土壤体积质量变化,进而对土壤水分特征曲线进行校准。土壤在吸水和失水时常常伴随膨胀和收缩[18],本研究测定的土壤水分特征曲线为脱湿曲线,然而由于滞后效应,关于土壤吸湿曲线校准与吸水条件土壤体积质量、含水率和吸力关系的研究有待进一步开展。同时有必要对比分析未校准与经过校准的水分特征曲线对土壤水流运动模拟精度的影响,进而印证考虑土壤体积质量变化的合理性。
4 结论
辽宁砂壤土(LN)、云南黏壤土(YN)、陕西黏壤土(SX)和山东壤土(SD)在脱水过程中,土壤含水率随吸力增加(0~7000 cm)而呈减小趋势,其减小速率基本整体呈现出“慢-快-慢”的变化特点,并以YN土样表现效果最为显著;Brooks-Corey模型可以较好地描述4种土壤的含水率与吸力之间的关系;在土壤脱水过程中,土壤体积质量与吸力之间呈幂函数关系;土壤体积质量与含水率呈负相关关系;4种土壤收缩变化均大致可划分为伪饱和段、结构段和超正常段等3个收缩段,各收缩段均满足直线型函数,但对于不同土壤各收缩段的吸力范围存在差异,为保证拟合曲线的连续性,可采用Logistic模型进行拟合。
参考文献:
[1]雷志栋,杨诗秀,谢森传.土壤水动力学[M].北京:清华大学出版社,1988:18-24.
[2]郑健,王燕,蔡焕杰,等.植物混掺土壤水分特征曲线及拟合模型分析[J].农业机械学报,2014,45(5):107-112.
[3]陶高粱,张季如,庄心善,等.描述黏粒含量对土-水特征曲线影响规律的分形模型[J].水利学报,2014,45(4):490-496.
[4]MOHAMMADI M H,MESKINI-VISHKAEE F.Predicting soil moisture characteristic curves from continuous particle-size distribution data[J].Pedosphere,2013,23(1):70-80.
[5]邢旭光,赵文刚,马孝义,等.土壤水分特征曲线测定过程中土壤收缩特性研究[J].水利学报,2015,46(10):1181-1188.
[6]LI X,LI J H,ZHANG L M.Predicting bimodal soil-water characteristic curves and permeability functions using physically based parameters[J].Computers and Geotechnics,2014,57(4):85-96.
[7]YANG S,LU T H.Study of soil-water characteristic curve using microscopic spherical particle model[J].Pedosphere,2012,22(1):103-111.
[8]VAN GENUCHTEN M T.A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J].Soil Science Society of America Journal,1980,44(5):892-898.
[9]BROOKS R H,COREYAT.Hydraulic properties of porous media[M].Montreal:McGill-Queen’s University Press,1964:352-366.
[10]魏玉杰,吴新亮,蔡崇法.崩岗体剖面土壤收缩特性的空间变异性[J].农业机械学报,2015,46(6):153-159.
[11]邢旭光,柳烨,马孝义.土壤添加物对土-水曲线和土体收缩的影响[J].水科学进展,2016,27(1):40-48.
[12]CRESCIMANNO G,PROVENZANO G.Soil shrinkage characteristic curve in clay soil:measurement and prediction[J].Soil Science Society ofAmerica Journal,1999,63(1):25-32.
[13]吕殿青,邵明安,王全九.土壤持水特征测定中的容重变化及其确定方法[J].水利学报,2003,34(3):110-114.
[14]MCGARRY D,MALAFANT K W J.The analysis of volume change in unconfined units of soil[J].Soil Science Society of America Journal,1987,51(2):290-297.
[15]FU X,SHAO M,LU D,et al.Soil water characteristic curve measurement without bulk density changes and its implications in the estimation of soil hy draulic properties[J].Geoderma,2011,167/168:1-8.
[16]吕殿青,王宏,王玲.离心机法测定持水特征中的土壤收缩变化研究[J].水土保持学报,2010,24(3):209-212,216.
[17]NELDER JA.An alternative form of a generalized logistic equation[J].Biometrics,1962,18(4):614-616.
[18]MOHAMMADI,M H,MESKINI-VISHKAEE F.Predicting soil moisture characteristic curves from continuous particle-size distribution data[J].Pedosphere,2013,23(1):70-80.
[19]ZHOU W H,YUEN K V,TAN F.Estimation of soil-water characteristic curve and relative permeability for granular soils with different initial dry densities[J].Engineering Geology,2014,179(11):1-9.
[20]邢旭光,马孝义.土壤失水过程对土体收缩特性的影响[J].农业机械学报,2016,47(6):148-153.