刘晓东1，韩 宇1*，邱流潮1，于 洋2
（1.中国农业大学，北京100083；2.清华大学，北京100084）
摘要：【目的】揭示明渠水流外区域流速分布偏离传统对数定律的潜在机理。【方法】基于猝发现象，根据雷诺纳维-斯托克斯方程推导出了描述明渠水流流速分布的改进模型，并通过多组试验工况对改进模型的准确性进行了验证。【结果】①该模型的分析结果与明渠中内/外区域的流速分布均吻合较好，仅有1.1%左右的误差；②将试验结果与当前应用较为广泛的YL、ML和CL定律对比，这些定律预测的结果与外层区域的实测数据相比分别存在3.1%、4.5%、5.2%左右的误差。【结论】二维均匀流中存在尾流定律的原因来自于流速的上下紊动，这种紊动造成外区水流的流速微降。
关 键 词：流速分布；明渠；湍流；对数定律；猝发现象
明渠水流流速分布是水动力学研究的主要问题之一，其流速分布特性对预防渠道的冲刷与淤积、水资源的合理配置、优化灌区用水管理系统等方面具有重要意义[1]。明渠水流大多为紊流，紊流流速分布的精准预测一直是研究人员重点关注的问题。自普朗特的边界层理论后，流速分布研究取得了非常大的进展。明渠中的水流可分为黏性底层区、过渡区、紊流粗糙区3个区，黏性底层区的流速呈线性分布，但黏性底层区和过渡区只占整个区域很小的一部分[2]。Kelulegan[3]将普朗特的边界层理论的研究成果应用到明渠水流流速分布的研究中，得到对数定律，即：
式中
，其中u*为平均摩阻流速；u为距渠底y处的流速（m/s）；v为流体的运动黏性系数（m2/s）；k为卡门系数。当u=0时，y=y0。系数y0是一个常数，与壁面的粗糙度有关。
近年来，关于明渠水流流速分布规律的研究多为理论和试验方向，传统的对数定律已经不能准确地描述明渠水流流速分布[4]。为此，研究人员分别针对平整和粗糙底面的水流流态进一步对尾流函数和对数定律进行改进来预测流速分布[5]。其研究方法主要分为3大类，第一类是在大量试验基础上拟合出尾流函数，Coles[6]提出纯经验的对数修正公式，与对数定律相比，尽管在外层区域其流速分布的预测精度略有提高，但是对于不同渠道宽深比及糙率的水槽，其预测结果依然存在较大的误差，同时尾流函数的准确性也缺乏理论支持。第二类是针对Coles理论公式存在的缺陷，Nezu等[7]研究发现对数定律只适用于近壁处内层区域（b/h＜0.6），但没有明确给出外区域流速的分布情况。随后有研究认为，这种流速微降的现象与明渠的结构特性有关，并提出流速微降现象不仅出现在主流中也出现在二次流中，主要受纵横比以及渠道结构的影响，当明渠水流宽深比b/h＜5时，流速微降现象则更为明显[8]，为此，通过建立尾流函数与渠道糙率、宽深比等变量之间的联系来简化尾流函数。但不存在一个通用的函数适用于各种宽深比及糙率的渠道，其预测偏差的存在也表明尾流函数中可能涉及更多的变量。第三类则更侧重明渠流速分布的预测在实际工程中的应用，韩金旭等[9]、王二平等[10]在田间试验的基础上，指出横向水流测线平均流速服从抛物线分布，简化了明渠测流工作量，但其表达式只适用于田间流量的粗略计算，不能解释外层区域流速偏离传统对数定律的原因。
目前，存在的研究方法均不能有效地解释明渠水流外层区域偏离传统对数定律的现象或其修正公式的应用范围受到局限，为了能够得到一个更为普遍的修正对数公式来预测整个明渠的流速分布情况，需要通过理论分析得出其流速分布偏离对数定律的潜在机理。
针对明渠水流流速分布偏离传统对数定律这一问题，常用包含尾流函数的修正对数定律描述流速分布规律。
Coles[6]针对该偏差通过提出完整的纯经验校正函数进一步完善对数定律，提出添加附加项作为对数定律的补充，以适应由尾流引起的流速偏离，即：
式中：II为分布系数，Coles发现对于0压力梯度的光滑边界层取系数II=0.55；h为水深。在明渠水流中，Kirkgoz[11]通过试验拟合该分布系数，得到非常小的值II=0.1。Tachie等[12]发现尾流系数不但与渠道边壁有关，同时也受自由水面的影响。Nezu等[7]认为应该将自由水面视为一种“弱壁面”，会对二次流的形成造成阻力。虽然试验得到的II取值与Coles原文献所记载的存在着很大的差别，但Coles提出的尾流定律仍为流速分布分析工作做出了巨大的贡献，尽管其原理以及尾流强度参数等还没有得到明确的解释。
从Coles得到的尾流函数中可以发现，CL定律的预测结果与实测流速存在正偏差，但Yang等[13]认为实测流速与对数律的预测结果存在负偏差，其最大纵向速度出现在水面以下，研究成果表明当存在流速微降现象时，Coles的尾流定律不能表示出整个区域的流速分布情况。Yang等[13]通过分析RANS方程提出了YL定律，这个定律的优点在于仅包含1个参数，计算简单。当α=0时，YL定律能与经典的对数定律很好的吻合。其在对数定律的基础上加一附加项来解释流速微降现象，并取代了Coles基于斯托克斯方程得到的尾流函数，即：
式中：b为渠道宽。
Lassabatere等[14]通过整合纳维斯托克斯方程，忽略流速在横向上的变化，提出了新的分析模型，该模型适用于不同的流态，同时也能较好地拟合外层区域的流速微降。即：
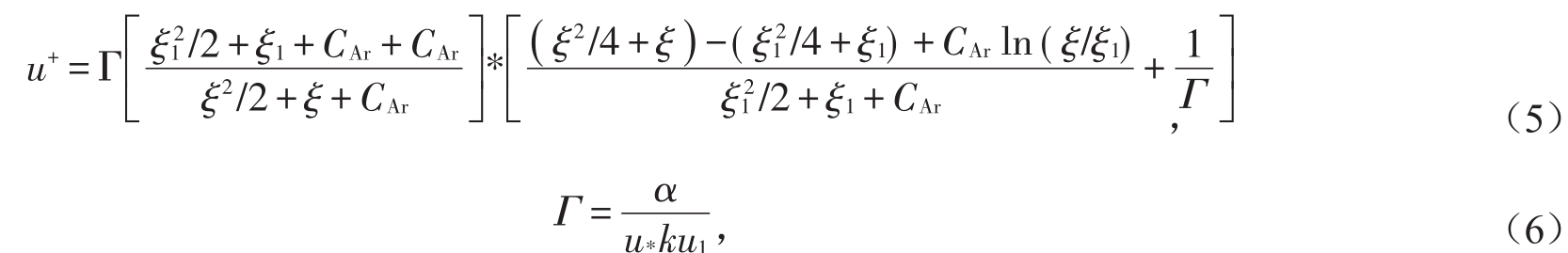
式中：u1为相对水深ξ1处的流速（m/s）；ξ为相对水深（m）；ξ1为层流上边界处的相对水深；α=ghθ，θ为渠道坡度；CAr是由试验条件确定的参数。对于粗糙和光滑渠底，该公式均能与流速微降现象下的主流流速分布实现较好的拟合，计算简单，适用于均匀流、充分发展的紊流等多种流态。但是CAr是渠道的形态特征和水流条件的函数，计算相对复杂，对于较复杂的试验条件，CAr可能会涉及更多的影响因素，其次该定律的预测结果与数值模拟结果存在一定的偏差。
Guo[15]认为对于光滑矩形明渠中的水流比经典的边界层流更为复杂，水流流速分布不仅受到渠底的影响，还受到渠边壁以及自由水面的作用。其基于2条假设研究流速微降现象：①随着明渠宽深比的变化，流速微降的位置从自由水面处到半水深处以指数形式下降；②明渠中垂线上的尾流函数与边界剪切力有关。同时提出了改进的流速分布公式ML，该定律符合流速微降情况下的流速分布规律。然而该定律不能用来预测流速分布，因为要求自由表面的流速符合抛物线分布以此获得流速下降的位置和最大流速值。正如他们所指出，该定律需要实测流速，所以ML定律只能应用流量测量，即：
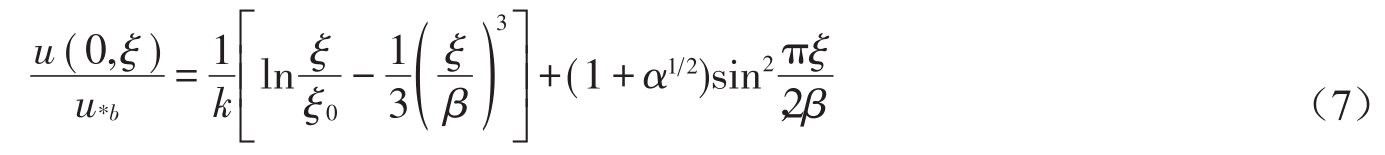
式中：
为无量纲的摩阻流速；ξ1为由对数定律得到的流速为零处的位置（m）；β为相对水深；α为自由表面剪切力与渠底剪切力的比值。
随着LDA及PIV等高精尖流速测量仪器的出现，紊动的水流实际上是由一系列排列有序的涡旋组成，称之为相干结构。相干结构可以分为2类：一类是发生在边壁处的猝发现象，一类是在外层区域水流的垂向运动。通过对相干结构的研究，基于速度波动现象研究了一种象限分析方法，即象限I：u’＞0和v’＞0；象限II：u’＜0和v’＞0；象限III：u’＜0和v’＜0；象限IV：u’＞0和v’＜0。Cellino等[16]认为应该重点关注象限III这种情况，因为紊流最重要的特征就是水流在壁面法线方向的紊动。其基于流速的紊动现象得到了一种计算平均紊动流速的新方法，然而象限分析方法和对数定律中流速偏离的关系还没有建立起来。Nezu等[7]发现在外层区域，平均流速的实测数据与对数公式整体发生较大偏离，在高雷诺数下，足够多的试验数据显示这种偏离在外层区域是不能被忽略的。针对此问题，学者们大多通过试验提出纯经验公式修正对数定律。对于不同的试验工况，这些对数定律需要做出相应的修正，不能找到一个能普遍适用的对数修正函数描述明渠水流流速分布。因此有必要通过理论分析去研究流速分布偏离对数公式的潜在机理。
本文的研究目的是根据平均雷诺纳维—斯托克斯方程分析明渠水流流速微降现象的潜在机理，基于猝发现象，寻求尾流函数与水流流速紊动之间的关系，推导出较为准确的对数修正函数，并通过试验验证该函数的准确性，这种新的研究方法能够解释外层区域流速偏移传统对数定律的现象，较好的描述明渠均匀流中的流速分布规律，为实际工程应用提供一定理论支持。
在恒定不可压缩三维明渠流动中，平均雷诺纳维—斯托克斯方程和连续方程的表达式分别为：
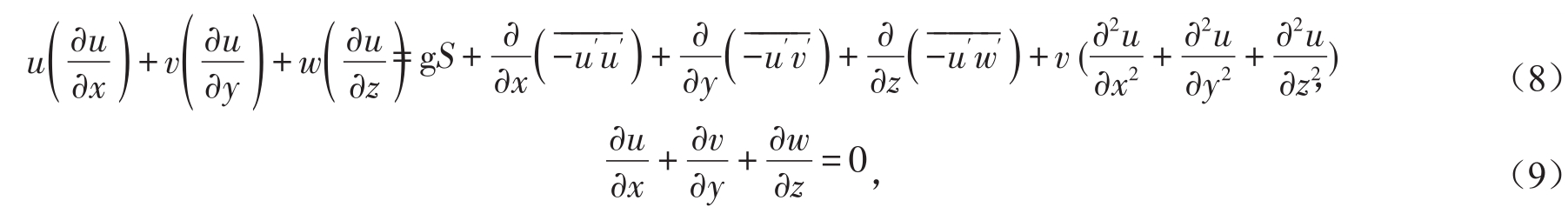
式中：u、v、w分别代表沿着水流流向x、侧向y、垂向z方向的流速（m/s）
为湍流切应力；s为坡度。对于充分发展的均匀水流而言，式（8）可以写为：
式（10）可以进一步写为：
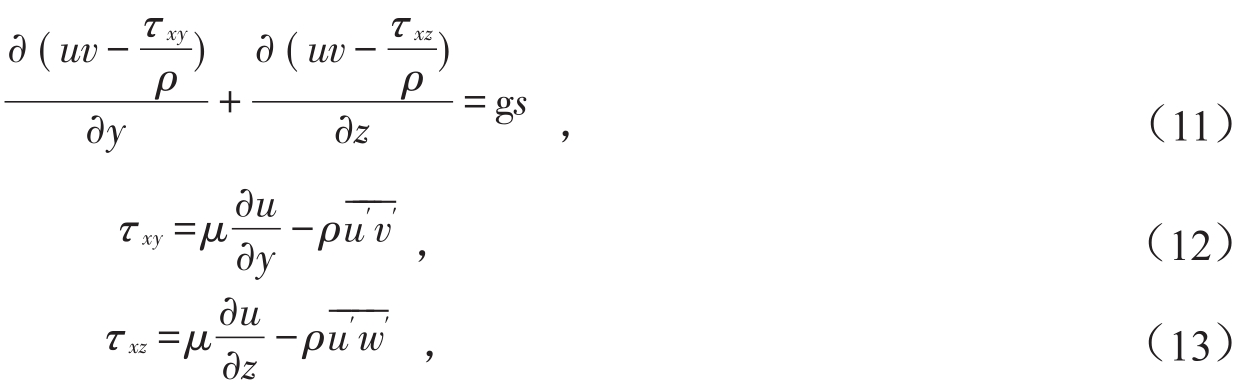
式中：τxy为y方向的切应力在x方向上的分量；ρ为流体密度；μ流体的黏性系数。在二维水流中，式（11）可简化为：
式（14）积分得到：
其中：C为积分常数，y=0时，v=u=0，以及
得到
因此在水面处y=h，v=0，摩阻流速为：
因此，动量方程可以写为：
其中
Yang等[13]研究了一种计算水流流速分布的新方法，即利用水流的猝发现象，但上述的时间平均方法不能用来解释猝发现象。为了解决这个问题，Yang根据水流流速的波动提出来一种计算平均紊动流速的方法，基于垂向流速的方向来确定猝发现象的可能性r，其中r定义为：
式中：Δt为获得2个连续流速数据的时间间隔；T为整个试验的观察时间，即T=ΣΔtu+ΣΔtd=Tu+Td。上下波动的流速可以用以下的方式定义：
式中：uu和ud分别代表向上和向下紊动的流速；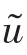
͂代表瞬时流速。雷诺剪切力的表达式为：
式中
为水深；u*u和u*d分别表示流速向上紊动和向下紊动情况下的摩阻流速。
涡流黏性Vt：
式中：ξ=y/h，将式（26）带入到式（24）中，得：
上下紊动流速梯度分别为：
相似的，平均流速梯度为：
将式（28）和式（29）带入到式（30）中得到：
又有：
得到：
则：
对式（35）积分得到：
由边界条件得：当u=0时，
得到：
最后得到描述明渠均匀流流速分布定律（DL），即：
DL定律中的参数A能有效地纠正对数公式中因水流流速上下紊动造成的流速偏离问题，从推导的对数公式中，确定了水流中尾流的存在。本文主要基于紊流的猝发现象，将流速分布的偏移问题和水流的紊动联系起来，推导得到流速分布公式。水流流速的上下紊动将紊流分为二部分，表明如果u+d=u+u，就可以得到经典对数公式，对于对数公式
，很多科学家从试验中得到了不同的参数k和B，式（38）表示造成这种结果的主要原因是水流紊动，因此必要通过试验数据证明DL定律的准确性。
本研究的主体试验(A1-4)是在澳大利亚伍伦贡大学的循环水槽中进行的，试验水槽长10.5 m，宽0.3 m，高0.45 m，水槽主要由储水池、玻璃水槽、循环管道以及泵组成，稳水蜂巢位于水槽的进水口处，槽中水深由尾水箱处的尾门控制，通过旋转把手控制尾门的相对开度，渠道底坡固定为0.1%，不同工况设置基于宽深比b/h变化，测量渠道断面中心线上流速分布沿垂向变化情况，从试验中可以得到三维湍流结构的速度、湍流强度，雷诺应力和边界剪切应力等数据。流速测量部分采用二维激光流速仪（LDA），具有60 mm光纤探头和前透镜，焦距为400 mm，且该系统由300 mW连续波氩离子激光器，包括分束器布拉格单元和信号处理器的发射光学器件组成。使用绿色（514.5 nm）和蓝色（488 nm）分量分别测量流速的水平和垂直分量，测量体积大约为0.189 mm×0.189 mm×3.97 mm。
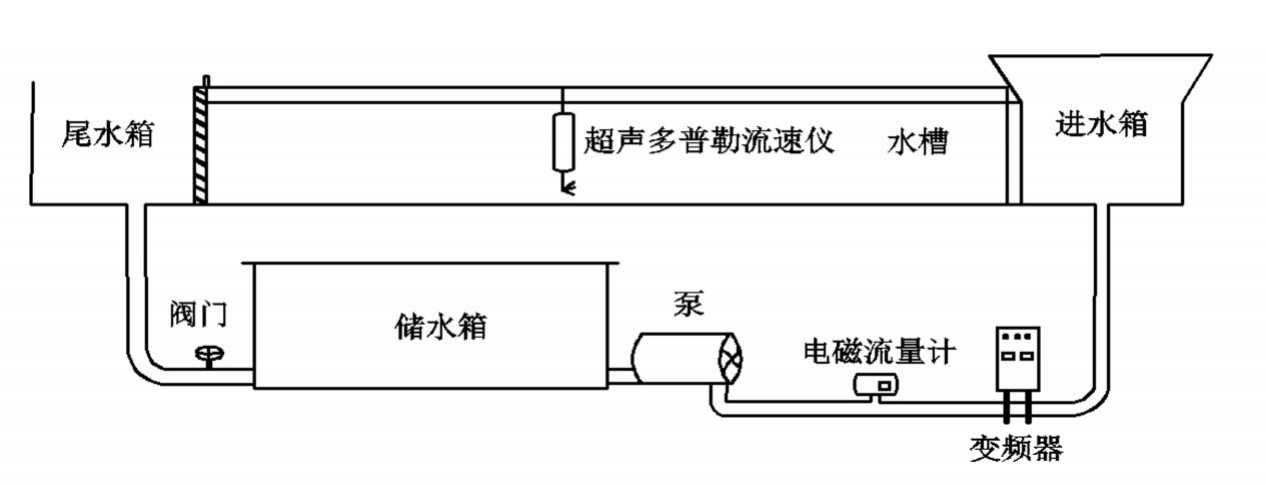
图1 循环水槽及CAD简图
部分试验（C1-2）在中国农业大学水利试验大厅的循环水槽中进行，试验装置由测流装置、控制装置、供水设备及循环装置组成。测流装置主要包括超声多普勒流速仪ADV（WIM-@ADV305），可获得水渠中三维流速、电磁流量计（LDTHS-200B10177JYLF62O1O）、测压管。控制装置主要包括变频器、尾门、过水栅。供水设备及循环装置主要包括储水池（4.1 m×1.2 m×1.2 m）、进水箱、玻璃水槽（6.3 m×0.8 m×0.6 m）、循环管道等组成。为保证进水口水流尽可能均匀，进水箱与水槽的中心线对齐，并且关于水槽的中心线对称。变频控制器可以根据试验需要提供所需的流量，流量的大小可以由电磁流量计读出。渠道底坡固定为0.1%。基于宽深比设置不同的试验工况，测量明渠横断面上中心线上的流速分布情况。图1为试验结构简图。
试验基于不同的宽深比（b/h）得到相应的工况，在均匀流条件下从渠底到自由水面按照适当的间距选取明渠横断面中垂线上测点，将得到的试验数据与DL、YL、CL及ML定律所预测的结果进行对比，图2给出了光滑明渠中各测点x方向的流速值与各定律的对比情况，对比结果显示所有的修正函数均能与内层区域的流速数据吻合较好，但在外层区域YL、CL及ML定律的预测结果与试验点发生了整体性偏移，通过试验结果也能很清晰地发现尾流函数确实存在于均匀流中。
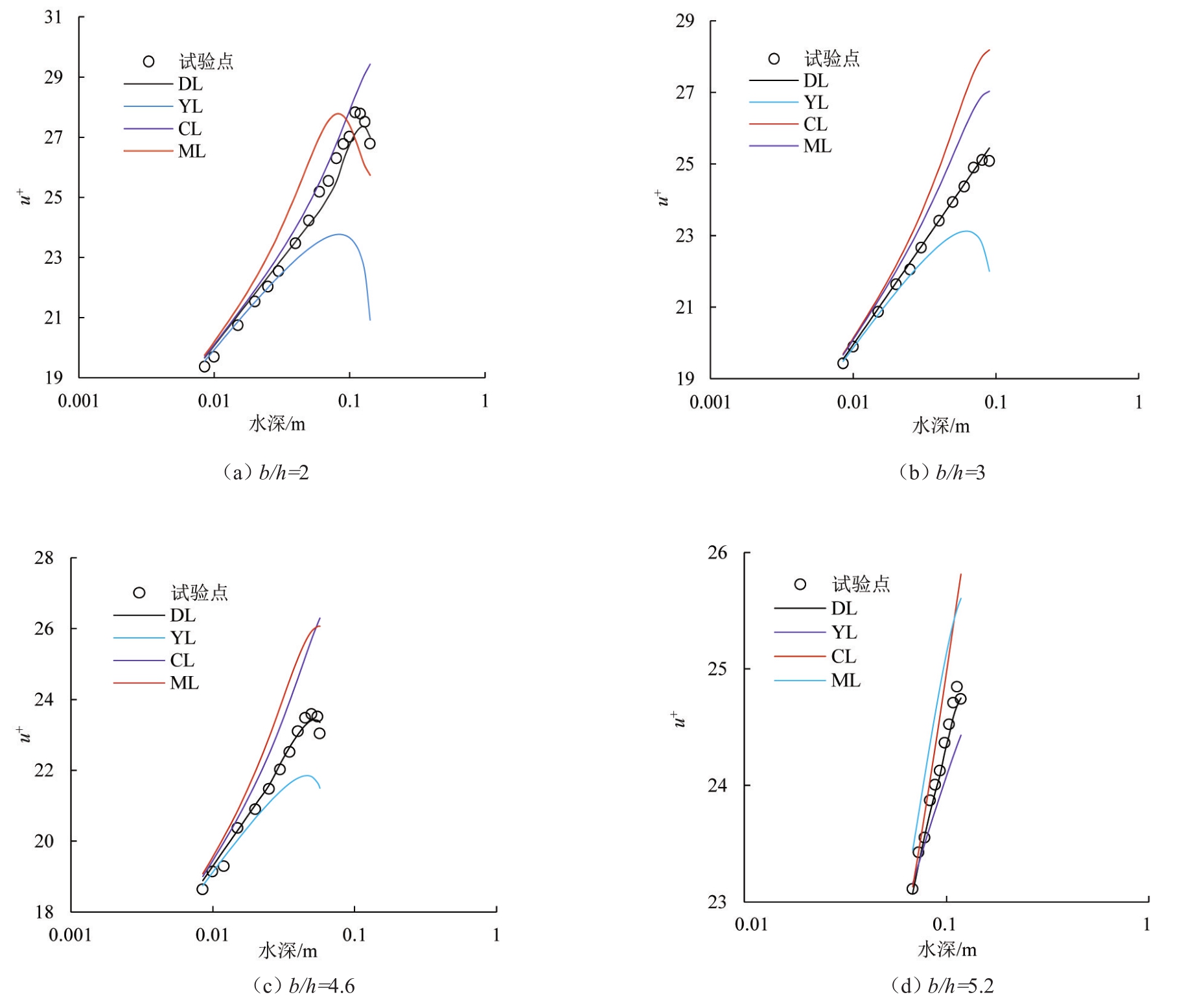
图2 光滑明渠中垂向各测点x方向的流速与各定律的对比情况
从图2可以发现，外层区域所测得流速数据要比YL定律所预测的结果偏高，由于不能通过调整YL定律中的参数α来提高其预测的准确性，所以式（3）需进一步改进。YL定律能够预测流速微降现象，但是对于最大流速的预测则显得不是很准确。因此对于流速微降现象的精确预测需要一个调整参数。CL及ML定律也能预测流速微降现象，但明显高估了外层区域的流速分布，对于外层区域这2种方法似乎都不是合适的预测方法。尽管CL定律对外层区域微降现象流速的粗略预测是很重要的，但仍表明II=0.55的值并不能提高预测精度。然而无论内层区域还是外层区域，DL定律均能与试验点实现较好地吻合。
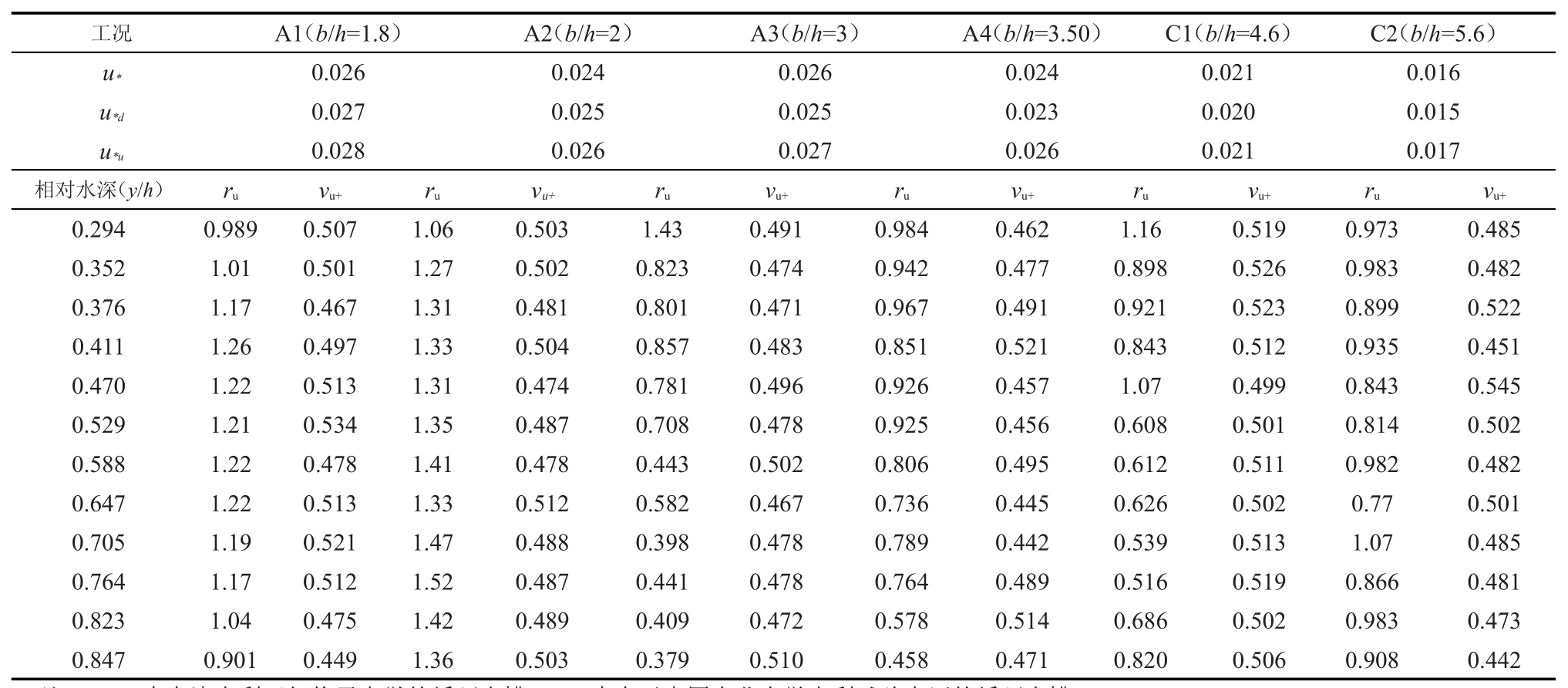
DL定律中的参数A对提高预测流速分布的精度是很重要的1个参数。如果要通过理论公式表示整个水槽的流速分布状况，首先要准确确定式（34）中的参数A。式（34）中的vu+和ru能够通过式（22）和式（18）准确的计算得到，公式中u*代表平均摩阻流速，u*=(grS)1 2，未知u*u和u*d以各自通过底坡被估计出来。则
u*u、u*d都可以通过计算得到，结果如表1所示。
表1 系数A在不同工况下的参数汇总
注 A1-4来自澳大利亚伍伦贡大学的循环水槽，C1-2来自于中国农业大学水利试验大厅的循环水槽。
基于试验数据可分别得到uu、ud、u*u和u*d，则uu+和ud+可以分别计算出来。式（34）中的系数uu+和ud+的比值在外层区域均大于1，因此A在外部区域都是负的。DL定律中尾流函数在外部区域也是1个负值，这表明DL定律中的流速一定低于对数定律所预测的流速，或者在水表面处存在流速微降现象，这表示水流上下紊动将引起尾流函数。在二维水流中，尾流定律是存在的，是由边壁处的流速紊动所引起的。将不同的系数A带入理论公式中，同时比较各公式的理论值与试验值的吻合度。表2汇总了各公式在几组工况下理论值与试验值的相对误差，结果显示DL定律的计算值与各组试验结果相比仅存在着1.1%左右的平均误差，相对于其他学者提出的理论公式误差较小，因此式（34）中的系数A完全能够解释对数定律所存在的偏差。
表2 几组工况下理论值与试验值的相对误差
同样，试验数据中获得β=uu+-ud+。将以上的分析应用到式（34）中，便可以得到所有的参数A。从图3可以看出，对于不同水深A和β之间的关系是相似的，呈对数分布规律，为了简化DL定律，需进一步建立参数A与相对水深（y/h）、宽深比（b/h）之间的关系简化尾流函数。
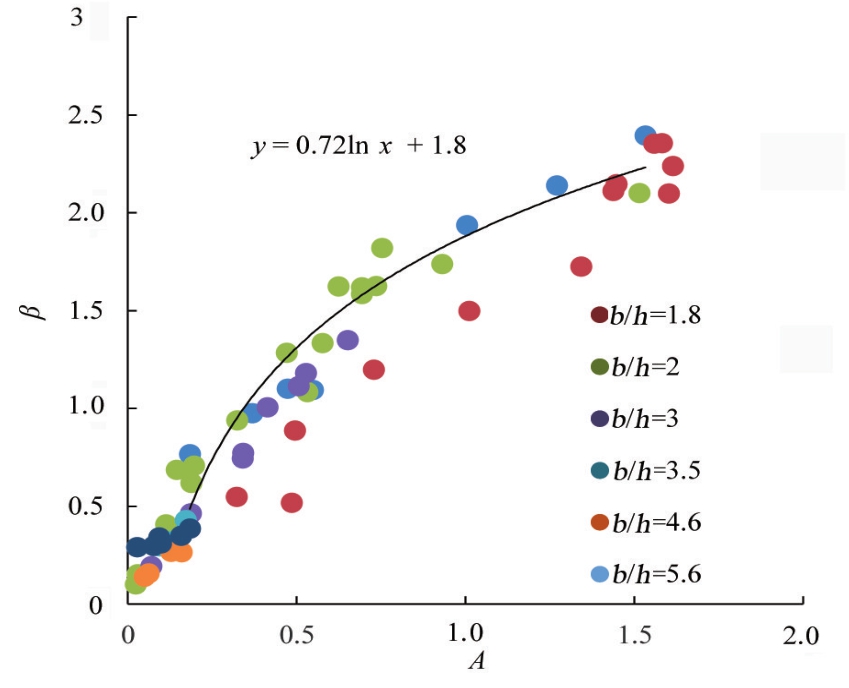
图3 不同工况下的A与β的关系图
式（35）中A为vu、ru、uu+和ud+的函数，虽然该式的预测流速与外层区域的试测数据吻合较好，但是A涉及的参数较多，且这些参数计算起来复杂。因此需要通过建立起A与y/h、b/h之间的联系简化尾流函数。基于不同的b/h，设定相应的试验工况，寻求A与y/h的定量关系，图4为不同工况下A与b/h、y/h的关系图。
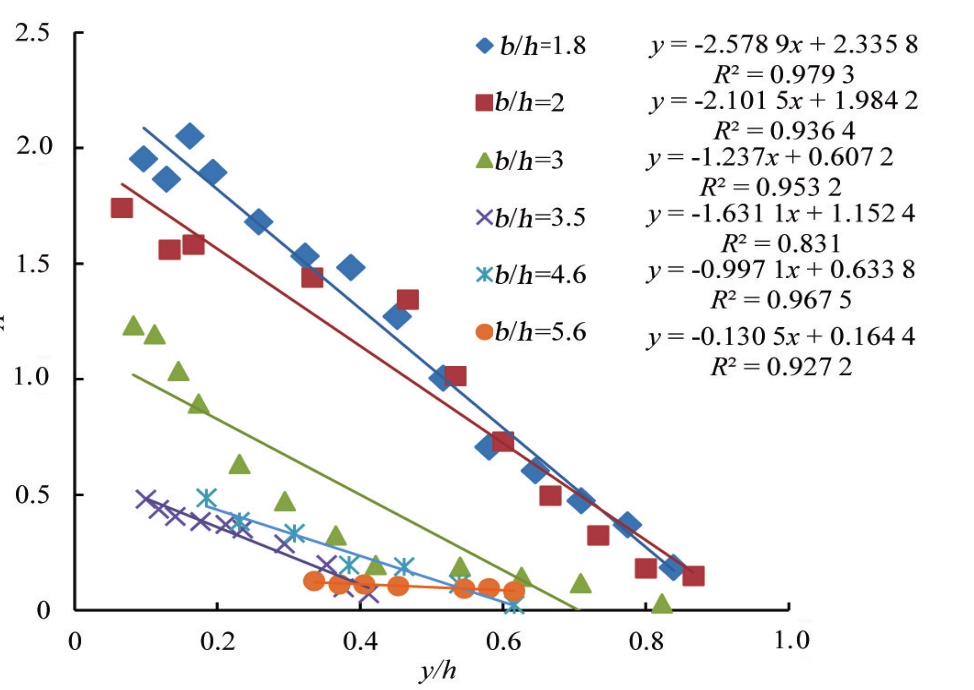
图4 不同工况下A与b/h、y/h的关系图
分别用对数关系和线性关系拟合宽深比(b/h)与参数c、d的关系，选取拟合效果较好的一组。残差R2作为评价拟合公式准确性的重要依据，根据2组拟合公式的残差得到参数c、d与b/h分别本采用对数和线性2种拟合方程，参数c对于2种拟合公式的残差较为接近以及考虑到公式的简化问题，因此参数c依然采用线性拟合。设A的线性简化方程为：
式中：c、d为参数，分别由拟合方程：c=-0.54(b/h)+3.24，d=-0.53(b/h)+2.9得到A的简化公式：
从式（40）可以发现尾流函数不仅与相对水深有关还与明渠的宽深比有关，与前人得到关于明渠水流流速分布会受到宽深比等因素影响的结论相吻合。将式（40）带到式（38）中，便得到简化后的流速分布公式。将简化公式与试验点对比，结果表明该简化公式有效的拟合外层区域的流速分布规律，并与YL、CL及ML定律做对比，图5结果表明，简化公式预测的流速分布相对其他公式与实测值更为接近。2组工况下简化定律的计算值与试验值的平均相对误差约为1.5%，尽管比DL定律的相对误差偏大，但在误差允许的范围内，该简化公式能更有效地应用到实际工程中，为工程应用提供理论支持。
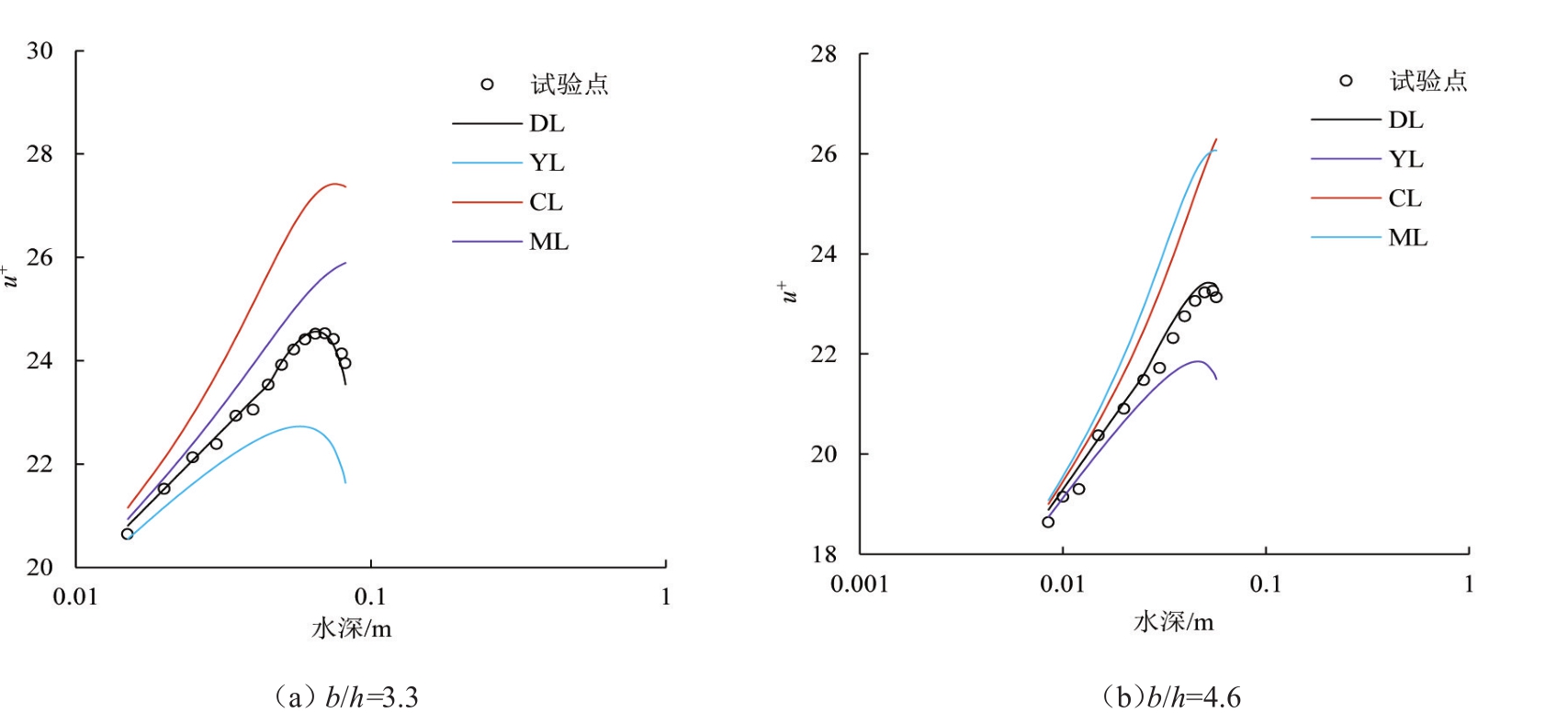
图5 光滑明渠中垂向各测点x方向的流速值与各定律的对比情况
前人对于外层区域流速偏离传统对数定律现象的研究大多是在大量试验基础上，拟合出尾流函数，得到的纯经验公式，或从明渠边壁粗糙度、宽深比等方面考虑修正对数函数，由于尾流公式涉及的更多变量被忽略，所以其理论值与试验值依然存在一定差异。总之前人得出的修正公式本质上都是经验公式，公式的应用受到限制同时也缺乏理论的支持，并没有从理论上分析造成外层区域流速发生微降的潜在机理。
本文基于水流的猝发现象，以平均雷诺纳维-斯托克斯方程和连续方程为理论依据，结合计算水流向上/下紊动的方法，研究外层区域水流流速分布偏离传统对数定律的潜在机理，指出外层区域流速分布偏离对数分布正是水流流速上下紊动的结果，并提出表达流速分布的新定律（DL)，其定律的准确性也通过相应的试验得到的证明。本文提出的DL定律能较好地预测明渠水流内区及外区的流速分布规律，DL定律与各工况下试验值的平均相对误差仅为1.1%左右，比其他理论公式的相对误差小得多。
DL定律尽管在试验条件下能够精确的预测流速分布，但定律中涉及几个计算复杂的参数，在实际工程中的应用将受到一定的局限。因此需要建立尾流函数中的参数A与b/h、y/h简化DL定律中参数A的计算，但由于试验条件的限制，只能设计有限的试验工况对本文的定律进行验证，其尾流函数简化是否合理还需要通过大量试验进一步的验证以及对于实际明渠中的复杂的水流条件，该定律的应用会受到怎样的限制，怎样将该定律更有效地应用到实际工程应用中，还需要更为深入研究，在理论公式的基础上提出更为有效的分析模型。
参考文献：
[1]韩金旭,李敬茹,杜凯,等.明渠水流测线平均流速横向分布及其应用[J].灌溉排水学报,2013,32(3):71-73.
[2]刘春晶,李丹勋,王兴奎.明渠均匀流的摩阻流速及流速分布[J].水利学报,2005,36(8):950-955.
[3]KELULEGAN G H.Laws of turbulent flow in open Channels[J].Journal of Research of the National Bureau of Standards,1938,21(6):707-741.
[4]雒天峰,吕宏兴,张春景,等.U形渠道横向流速分布规律及测流技术研究[J].灌溉排水学报,2008,27(1):61-64.
[5]陈兴伟,林木生,林炳青.粗糙透水床面明渠水流垂线流速分布的试验研究[J].亚热带资源与环境学报,2012,7(4):16-19.
[6]COLES D.The law of the wake in the turbulent boundary layer[J].Journal of Fluid Mechanics,1956,1(2):191-226.
[7]NEZU I,RODI W.Closure of“open-channel flow measurements with a laser doppler anemometer”[J].Journal of Hydraulic Engineering,1987,113(12):1574-1576.
[8]BAI Y,WANG X.Theoretical bend-flow solutions and velocity-dip phenomenon[J].Journal of Hydraulic Research,2016，55(3):1-11.
[9]韩金旭,李敬茹,杜凯,等.明渠水流测线平均流速横向分布及其应用[J].灌溉排水学报,2013,32(3):71-73.
[10]王二平,金辉,张艳艳,等.矩形明渠流速分布特征及其在流量量测中的应用[J].灌溉排水学报,2008,27(4):25-28.
[11]KIRKGOZ M S.Turbulent velocity profiles for smooth and rough open channels-closure[J].Journal of Hydraulic Engineering,1991,117(9):1221-1222.
[12]TACHIE M F,BALACHANDA R,BERGSTROM D J.Low Reynolds number effects in open-channel turbulent boundary layers[J].Experiments in Fluids,2003,34(5):616-624.
[13]YANG S Q,LIM S Y,TAN S K.Velocity distribution and dip-phenomenon in smooth uniform open channel flows[J].Journal of Hydraulic Engineering,2004,130(12):1179-1186.
[14]LASSABATERE L,JANN HUI P U,BONAKDARI H,et al.Velocity distribution in open channel flows:an analytical approach for the outer region[J].Journal of Hydraulic Engineering,2013,139(1):37-43.
[15]GUO J.Modified log-wake-law for smooth rectangular open channel flow[J].Journal of Hydraulic Research,2014,52(1):121-128.
[16]CELLINO M,LEMMIN U.Influence of coherent flow structures on the dynamics of suspended sediment transport in open-channel flow[J].Journal of Hydraulic Engineering,2004,130(11):1077-1088.
Velocity Distribution within Open Channel Studied Using the Average Structure of Turbulent Flow
LIU Xiaodong1,HAN Yu1*,QIU Liuchao1,YU Yang2
(1.ChinaAgricultural University,Beijing 100083,China;2.Tsinghua University,Beijing 100084,China)
Abstract:【Objective】The objective of this paper is to disentangle the underlying mechanisms that the distribution of water velocity in the outer region of open channel deviates from the log-law.【Method】We developed a new analytical model,similar to the Reynolds’average Navier-Stokes equations,by considering the bursts,and then verified it against experimental data.【Result】①The results calculated from the proposed model agreed well with the measured velocity distribution in both internal and outer regions of the channel with an error of 1.1%.②Compared with experimental velocity distribution,the errors resulted from the commonly used YL,ML and CL law in the literature were 3.1%,4.5%and 5.2%respectively,much higher than the error of the proposed model.【Conclusion】The underlying mechanisms of the wake law in 2D uniform channel flow is the result of up-down events,and such a turbulent flow slightly reduced the velocity in the outer region of the open channel.
Key words:velocity distribution;open channel;turbulence;log-law;bursting phenomenon
责任编辑：白芳芳
中图分类号：TV131.2
文献标志码：A
doi:10.13522/j.cnki.ggps.2017.0455
刘晓东，韩宇，邱流潮，等.基于平均紊动结构下明渠水流流速分布的研究[J].灌溉排水学报，2018，37（8）：106-114.
文章编号：1672-3317（2018）08-0106-09
收稿日期：2017-07-30
基金项目：国家自然科学基金青年科学基金项目（51509248）；中国农业大学基本科研业务费专项资金项目（2015QC025,2017SL001）；“十三五”国家重点研发计划项目（2016YFC0400200，2017YFC0403203）
作者简介：刘晓东（1993-），男。硕士研究生，主要从事水工结构方向研究。E-mail:2427817067@qq.com
通信作者：韩宇（1985-），女。讲师，主要从事生态明渠水流特性方向研究。E-mail:44917228@qq.com