0 引言
降雨量是开展水资源管理、城市内涝预警以及水文分析的重要参数。对降雨量进行预测可为农业、水利等相关部门提供决策依据[1-2]，具有重要的理论意义和实用价值。降雨量预测模型可分为物理模型和数据驱动型模型。物理模型根据物理定律模拟与降雨相关的物理过程进行降雨量预测，数据驱动模型则通过挖掘历史数据变化规律预测降雨量。由于降雨是极为复杂的水文过程，受海洋、大气及陆地表面特征等相互作用影响，导致很难构建准确的物理模型，而基于数据驱动的降雨量预测模型更具适用性。
在数据驱动预测方法中，自回归移动平均模型（ARIMA）与人工神经网络（ANN）被广泛用于降雨量预测。例如：Narayanan等[3]应用AIRMA模型对印度地区季风期降雨量进行预测，得出季风期降雨量存在增长趋势；Kim等[4]应用ARIMA模型预测了蒙古地区季度降雨量，其预测结果与实际变化趋势基本一致。然而，ARIMA模型只对具有自相关性、趋势性或季节性的季度降雨量有较高预测精度[5]，而对非线性、非平稳的月降雨量预测精度较低。考虑到神经网络技术对非线性时间序列具有较高预测精度，Abbot等[6]应用神经网络模型预测了澳大利亚昆士兰地区的月降雨量，并表明神经网络模型预测精度高于当前澳大利亚官方使用的预测方法；Deo等[7]利用人工神经网络预测了澳大利亚东部的月平均降水量和蒸散指数。Bagirov等[8]对比了聚类回归（CLR）、最大期望回归（CR-EM）、多元线性回归（MLR）、支持向量机回归（SVMreg）及神经网络（ANN）5种方法对澳大利亚维多利亚8个站点的月降雨量预测精度，结果表明，针对不同降雨时间序列，不同算法预测精度不同，其中ANN对3个城市的月降雨量表现出最佳预测精度，聚类回归对5个城市的月降雨量有最佳预测效果，SVMreg及MLR算法分别对1个城市具有并列最佳预测效果。此外，上述5种算法预测结果的平均绝对误差均值约20 mm，最大平均绝对误差高达28.6 mm。由此可见，虽然目前学者对月降雨量预测开展了广泛研究，但如何进一步提高预测精度仍值得研究。
鉴于单一预测模型对非线性、非平稳时间序列预测精度偏低，许多组合预测模型[9-11]被研究人员提出。数据融合是一种具有代表性的组合预测技术[12]，其通过融合多源数据深入挖掘时间序列变化趋势，进而提高预测精度。在水文研究领域，基于数据融合的预测方法被广泛用于水库日流量、月流量预测[13-14]，但在降雨量预测方面的应用尚未见报道。鉴于此，提出一种基于数据融合的月降雨量预测方法，将月降雨量时间序列分为月降雨量和年降雨量子序列。根据这2个序列的不同特点，分别选取灰色模型（EGM）和自适应模糊神经网络系统（ANFIS）进行预测，再利用灰色关联法对2个预测结果进行数据融合。为验证所提出方法，采用文献[8]中澳大利亚维多利亚8个站点实测降雨数据，将所提出方法预测结果与其他方法预测结果进行对比。
1 数据驱动下基于模型融合的月降雨量预测
降雨量存在显著的周期性、季节性及趋势性；同时，随机干扰和天气条件不断变化，导致降雨量在不同时间尺度上呈现不同模式。鉴于月降雨量非线性、多尺度特征，采用数据融合方法提高降雨量预测精度，其基本思路是在年和月时间尺度上分别预测月降雨量，然后进行数据融合。具体地，在年时间尺度上，考虑到降雨的周期性及季节性，将历史年中相同月份降雨量组成子序列预测当前月降雨量；在月时间尺度上，考虑降雨的趋势性及随机性，利用相邻月降雨量预测当前月降雨量，然后将2个预测值进行数据融合。基于数据驱动的预测模型可采用下列表达式：
式中：y1(t)、y2(t)分别为年尺度及月尺度下第t个月降雨量预测值；x(t)为月降雨量实测值；F1[]及F2[]分别为对应的预测模型；τ1、τ2为时间延迟；d1、d2为嵌入维；y(t)为模型融合后月降雨量预测值；F[]为尺度归一化融合函数。对年尺度子序列，时间延迟τ1=1，嵌入维d1=1。对联系月降雨量序列，考虑到水文系统普遍具有混沌特性[15]，采用混沌相空间重构技术计算数据样本的时间延迟及嵌入维d2[16]。
1.1 基于灰色理论的年尺度下月降雨量预测
年尺度下月降雨量预测利用历史年份中相同月降雨量构成子序列预测当前月降雨量，其出发点是基于历史年中相同月份水文条件和气候条件大致相同，因此理论上具有准线性和准平稳的性质。考虑年尺度下的月降雨量子序列样本数通常较少（每年仅1个样本），兹采用灰色预测EGM(1,1)模型进行预测。灰色理论预测模型最早由邓聚龙[17]提出，在解决小样本、贫信息等问题上有其独特的优势，被广泛用于预测领域[18]。利用每年相同月份的月降雨量构成年尺度子序列：
，将该序列变换为
，其中n=1,2,…,d1。做1次累加生成序列
，其中
求均值序列
，其中k=2,3…,d1，则
建立均值GM(1,1)模型：
，其中a为平均发展系数，b为灰色作用量，可采用最小二乘法求得。可得基于灰色理论的月降雨量预测模型为：
1.2 基于自适应神经模糊系统的月尺度下月降雨量预测
如前述，受天气条件及随机干扰因素影响，月尺度下的月降雨量呈现较强非线性特征。Akrami等[19]关于月降雨量预测的研究表明，相较于传统神经网络，基于自适应神经模糊系统（ANFIS）的预测模型精度更高。鉴于此，采用ANFIS模型进行月尺度下的月降雨量预测。ANFIS模型最早由Jang等[20]提出，其将模糊逻辑推理和神经网络有机结合，适用于处理不确定、非线性和不适定问题，具有自适应学习能力强、收敛速度快和预测精度高等优点。采用具有2个输入
和1个输出y=y1(t)的模糊推理系统，满足如下IF-THEN规则：
式中：Am、Bm为特性标识（m=1、2）模糊神经网络结构及训练方法详见文献[20]。
1.3 基于灰色关联的数据融合
数据融合是将同一对象的多个预测结果关联、组合的过程，例如求均值或加权平均值。采用灰色关联作为数据融合工具，其以几何形状为基础对不同数据源进行融合，弥补了数理统计方法导致的预测误差。灰色绝对关联度的计算式[21]为：
式中：
其中x(l)、x(为样本序列的第l、M项；M为预测样本数；Y(l)=x(l)-x(1)、Yi(l)=yi(l)-yi(1)、yi(l)为i预测法的第l个预测值（i=2）。基于式（5），最终预测结果y计算式为：
2 降雨量预测实例
2.1 预测实例
采用文献[8]中维多利亚8个站点实测降雨数据验证所提出预测方法。这些数据为1889年1月—2014年12月的月降雨量，可从澳大利亚气象局网站上下载得到。将前1 392个月降雨量数据作为建模样本，后120个月降雨量数据作为检验样本。值得注意的是，在利用EGM(1,1)模型对年尺度下月降雨量预测时，需检验数据样本的级比λ(k)以保证预测模型的可靠性。具体地，若所有级比都落在可容覆盖
内，则表明预测模型可靠，否则需要对数据样本做变换处理。对数据进行变换处理时可将原数据叠加适当常数c，做平移变换。对8个站点116个月的降雨量数据建模，经平移变化后计算得出
满足建模要求。
2.2 预测精度检验
采用均方根误差、平均绝对误差以及Nash-Sutcliffe系数（NS）作为预测精度检验标准，计算式为：
均方根误差：
平均绝对误差：
Nash-Sutcliffe系数：
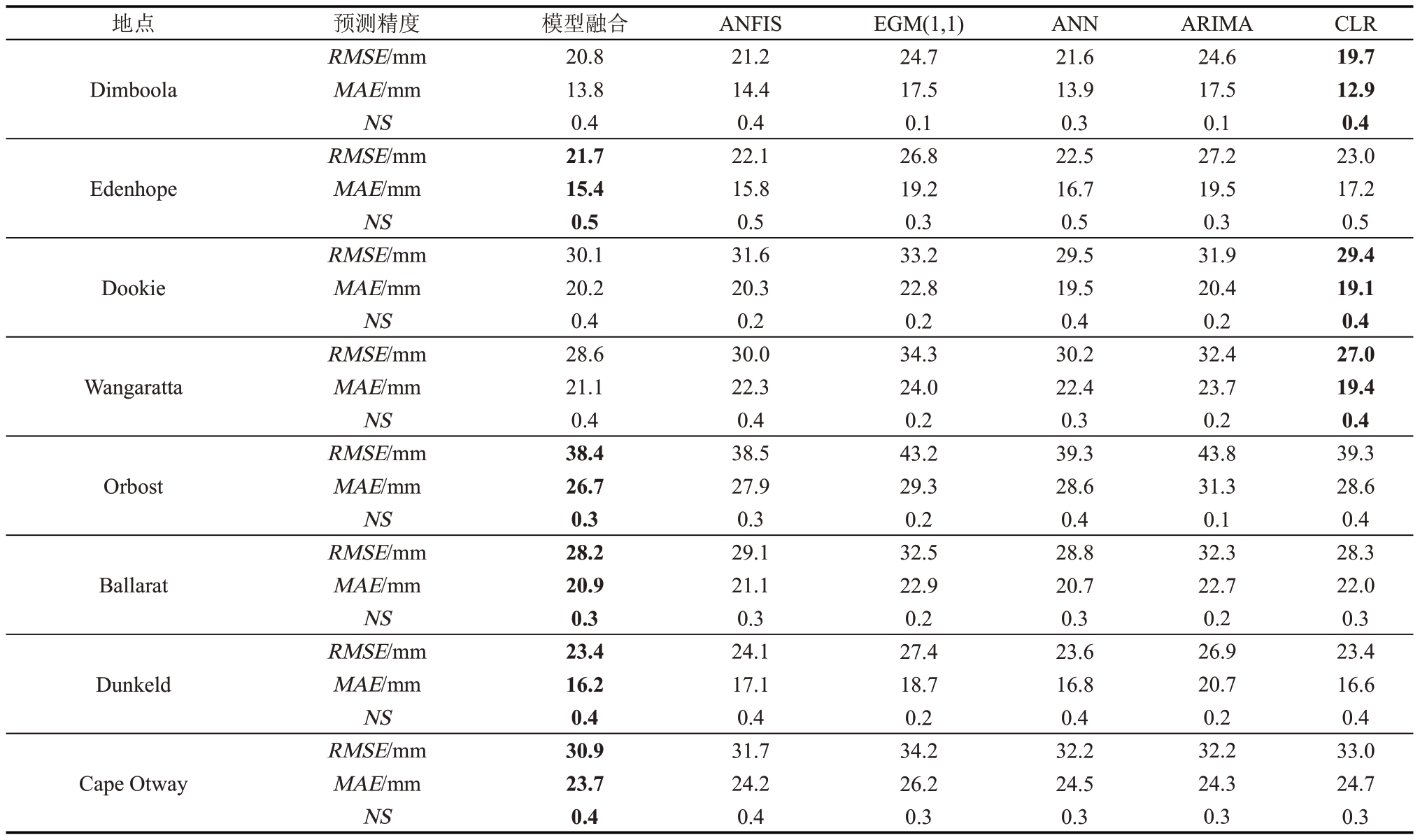
式中：m为样本数；X为月降雨量实测值；
为实测值的平均值；Y为月降雨预测值。如表1所示，除模型融合预测结果外，还给出了ANFIS、EGM(1,1)、ANN、ARIMA及文献[8]中CLR法等5种单一模型预测结果，其中最佳预测结果采用粗体字标识。
从表1可以看出，除Dimboola、Dookie及Wangaratta站点外，对其他5个站点的月降雨量，模型融合法都表现出最佳预测效果；另外，单一的ANFIS及EGM(1,1)模型预测精度都低于融合模型预测精度，这验证了所提出方法的可行性及优越性。此外，对所有站点，EGM(1,1)与ARIMA月降雨量预测精度都低于ANFIS及ANN预测精度，这是由于EGM(1,1)与ARIMA认为数据样本具有准线性和准平稳特征，而实际中受气候等随机因素影响，月降雨量呈现较强的非线性特征。通过比较上述8个站点预测结果还可得出，从西部到东部方向降雨量预测精度呈现较大差异，相对于中部地区（Ballarat和Cape Otway站点）及东部地区（Dookie，Wangaratta和Orbost站点，预测均方根误差为28.2～37.2 mm），西部地区预测结果更准确（Dimboola，Edenhope和Dunkeld站点，预测均方根误差为20.8～23.4 mm），其中沿海城镇Orbost的预测精度最低。这是由于东部天气比西部更多变，而沿海城镇气候变化最为复杂，导致降雨随机性更大，预测结果精度最低。限于篇幅原因，仅给出了Orbost地区各模型的预测结果，如图1所示。更多关于这些地区的气候特点及降雨量信息，可参见文献[8]。
表1 基于6种方法的8个站点月降雨量预测结果
?
图1 Orbost地区实测值与预测值
3 讨论
基于澳大利亚维多利亚8个站点降雨数据，对比了EGM(1,1)与ANFIS耦合模型、单一EGM(1,1)、ANFIS、人工神经网络（ANN）、自回归积分滑动平均模型（ARIMA）与聚类回归法（CLR）模型预测性能。研究得出，相较于其他预测模型，单一ANFIS能比较准确预测较大降雨，但对较小降雨的预测偏小。EGM(1,1)预测结果趋于平稳，这是由于EGM假设降雨量具有周期性及季节性，故无法准确预测气候突变时的大降雨，这与文献[13，19]结论相似。此外，由图1（d）与图1（f）可以看出，ANN模型及CLR模型对较大降雨量预测精度较高，而ARIMA模型对较大降雨量精度预测较低，这是由于前两者具有较强的非线性映射能力，而ARIMA模型更适用于自相关性、趋势性较高的时间序列，这与文献[8]研究结果一致。通过考虑月降雨量多尺度特征，融合模型预测在不利用其他信息的前提下能获得与CLR预测法精度相当的结果，这表明本文所提出预测方法是可行的。但值得注意的是，模型融合法对大降雨（如突发暴雨）的预测精度偏低，甚至不如单一模型预测结果。这是由于在数据融合过程中，为保证整体预测精度，一定程度上降低了大降雨预测精度，如何提高气候突变时的大降雨预测精度有待进一步研究。
4 结论
1）EGM(1,1)模型通过对原始数据进行一次累加及均值变换，使得其对小样本、贫信息、不确定性系统的预测具有独特优势，适用于数据样本较少的年尺度下月降雨量预测；ANFIS预测模型综合了神经网络和模糊推理优点，具有较强的非线性映射能力，适用于非线性特征较强的月尺度下月降雨量预测。
2）模型融合预测结果精度高于单一的EGM(1,1)、ANFIS、ANN及ARIMA模型预测结果，并在8个站点中的5个取得了最佳预测效果，聚类回归法（CLR）对Dimboola、Dookie及Wangaratta站点月降雨量具有更高预测精度，这表明所提出的模型融合预测法可行，但如何进一步提高月降雨量预测精度仍值得研究。
3）月降雨量预测精度一方面取决于预测模型本身，另一方面受区域气候影响较大，气候稳定的内陆月降雨量预测精度高于气候多变沿海预测精度，如何提高多变气候地区月降雨预测精度是未来研究方向。今后工作中，还应采用我国各地月降雨量实测数据进一步验证本文所提出方法。
[1]薛胜军,张佩云,陈静怡.云平台下基于半朴素贝叶斯的降雨量预测[J].系统仿真学报，2016，28(5):1 117-1 123.
[2]CHAU K W,WU C L.A hybrid model coupled with singular spectrum analysis for daily rainfall prediction[J].Journal of Hydroinformatics,2010,12(4):458-473.
[3]NARAYANAN P,BASISTHAA,SARKAR S,et al.Trend analysis and ARIMA modelling of pre-monsoon rainfalldatafor western India[J].Comptesrendus Géoscience,2013,345(1):22-27.
[4]KIM B S,HOSSEIN S Z,CHOI G.Evaluation of temporal-spatial precipitation variability and prediction using seasonal ARIMA model in Mongolia[J].Ksce Journal of Civil Engineering,2011,15(5):917-925.
[5]FAULINA R.Hybrid ARIMA-ANFIS for Rainfall Prediction in Indonesia[J].International Journal of Science&Research,2013.
[6]ABBOT J,MAROHASY J.Input selection and optimisation for monthly rainfall forecasting in Queensland,Australia,using artificial neural networks[J].Atmospheric ReseIarch,2014,138(2):166-178.
[7]DEO R C,SAHN M.Application of the Artificial Neural Network model for prediction of monthly Standardized Precipitation and Evapotranspiration Index using hydrometeorological parameters and climate indices in eastern Australia[J].Atmospheric Research,2015,161/162:65-81.
[8]BAGIROV A M,MAHMOOD A,BARTON A.Prediction of monthly rainfall in Victoria,Australia:Cluster wise linear regression approach[J].Atmospheric Research,2017,188:20-29.
[9]郑玉胜,黄介生.基于神经网络的灌溉用水量预测[J].灌溉排水学报,2004,23(2):59-61.
[10]廖凯华,徐绍辉,吴吉春,等.基于PCR和ANN构建的土壤转换函数的适用性研究[J].灌溉排水学报,2014,33(1):17-21.
[11]王翠翠,魏永霞.基于GM(1,1)-AR模型和AR模型的黑土区坡耕地土壤水分预测[J].灌溉排水学报,2014,33(z1):414-418.
[12]ZHANG Jixian.Multi-source remote sensing data fusion:status and trends[J].International Journal of Image and Data Fusion,2010,1(1):5-24.
[13]ABABAEI B,MIRZAEI F,SOHRABI T,et al.RESERVOIR DAILY INFLOW SIMULATION USING DATA FUSION METHOD[J].Irrigation &Drainage,2013,62(4):468-476.
[14]BAI Y,CHEN Z,XIE J,et al.Daily reservoir inflow forecasting using multiscale deep feature learning with hybrid models[J].Journal of Hydrology,2016,532:193-206.
[15]SIVAKUMAR B,BERNDTSSON R.Advances in data-based approaches for hydrologic modeling and forecasting[M].Singapore：WORLD SCIEN TIFIC,2010.
[16]任刚红,杜坤,刘年东,等.局域法邻近点选取对供水量预测精度的影响[J].土木建筑与环境工程,2017,39(4):102-106.
[17]邓聚龙.灰色系统理论教程[M].武汉：华中理工大学出版社,1990.
[18]JIN S H,LIN P,HALLETT M.Linear and nonlinear information flow based on time-delayed mutual information method and its application to cortico muscular interaction[J].Clinical Neurophysiology Official Journal of the International Federation of Clinical Neurophysiology,2010,121(3):392-401.
[19]AKRAMI S A,NOURANI V,HAKIM S J S.Development of nonlinear model based on wavelet-ANFIS for rainfall forecasting at Klang Gates Dam[J].Water Resources Management,2014,28(10):2 999-3 018.
[20]JANG J S R,SUN C T，MIZUTANI E.Neuro-fuzzy and soft computing-a computational approach to learning and machine intelligence[J].IEEE Trans.Autom.Control,1997,42(10):1 482-1 484.
[21]LIU S,FORREST J,YANG Y.A brief introduction to grey systems theory[C]//IEEE International Conference on Grey Systems and Intelligent Services[J].IEEE,2011，3：2 403-2 408.