0 引言
轴流泵属于低扬程泵型,具有流量大、扬程低等特点,广泛应用于农田灌溉、排水及大型水利工程等领域,在国民经济建设中发挥着重要作用。随着轴流泵机组容量的不断增大和转速的提高,其高速、多工况下的工作状况使得轴流泵转子稳定性相对降低、流场趋于复杂化,严重影响了轴流泵运行的可靠性[1-3]。因此,研究不同流量工况下轴流泵转子径向力及其内部流场压力脉动问题,不仅能够掌握轴流泵转子径向力及其内部压力脉动随流量变化规律,还可以有效预防径向力和压力脉动引起的轴流泵故障[4-6]。
目前,国内外学者对转子系统出现的径向力问题进行了广泛的研究。Adkins等[7]与Barrio等[8]通过理论分析、数值计算研究了离心泵转子的径向力分布情况。袁寿其等[9]为了改善单叶片螺旋离心泵叶轮上的受力情况,通过数值模拟的方法对螺旋离心泵的内部流场进行了数值计算,获取了螺旋离心泵的蜗壳出口压力脉动特性以及作用在叶轮和蜗壳上的径向力特性。杨敏等[10]通过数值计算方法研究了离心泵径向力,发现叶轮所受径向力分布不均匀,随着叶轮的相位变化呈现不稳定性。张亮等[11]采用叶轮出口压力法分析长短叶片叶轮双吸离心泵径向力。张肖等[12]对混流泵空化工况下叶轮径向力的变化情况进行了分析,结果表明,叶轮受到的瞬态径向力合力随着叶轮的转动呈现周期性变化,且频率与叶轮叶片数表现出相关性,但所受径向力的幅值却随空化程度加深而有所增加。但截至目前,国内外对轴流泵转子径向力研究较少,张琳等[13]通过分析潜水轴流泵的结构动应力,发现在偏离额定工况的小流量工况下,不平衡的情况较为明显,而在额定工况及大流量工况下,则显现出了较好的径向力平衡状态。
轴流泵内部压力脉动是引起机组振动和噪声的主要原因之一。在轴流泵内部压力脉动方面,宋希杰等[14]采用Fluent软件对轴流泵装置进行非定常计算,结合模型试验,利用高速摄像机对漩涡生成到消失全过程进行动态测量,观察到漩涡微观变化过程,得出了进水漩涡从生成到溃灭的过程及对压力脉动的影响。何乃昌等[15]对轴流泵不同工况下的外特性和压力脉动进行了测试,重点分析了轴流泵马鞍区水力特性和压力脉动特性。姚捷等[16]分析了叶轮叶片数对轴流泵压力脉动特性的影响,发现随着叶片数增多,周期性脉动明显减弱,随机信号逐渐增强。张德胜等[17]采用高频压力传感器对某一轴流泵模型进行了系列压力脉动测量试验,发现叶轮进口处的压力脉动主频均为叶频,但叶轮出口的压力脉动主频随着转速的变化而发生漂移,泵内最大压力脉动峰峰值在泵内的位置也随之改变。
为进一步研究轴流泵转子径向力及内部流动特性,通过ANSYS CFX定常计算和试验研究对比分析不同流量工况下轴流泵外特性,验证数值模拟的准确性。采用ANSYS CFX非定常数值计算不同流量工况下不同相位转子径向力,以同时监测不同位置处的压力脉动情况,探讨流量变化对轴流泵转子径向力和压力脉动的影响。
1 研究模型
1.1 计算模型
研究模型采用叶轮直径为300 mm的轴流泵,流量Q=300 L/s,扬程H=4 m,转速n=1 300 r/min,叶片数Z=4,导叶叶片数Zd=6。通过Pro/E软件对轴流泵模型进行三维建模,得到轴流泵的水体造型,计算区域为进口段到肘形进水流道,出口段为虹吸式流道,轴流泵装置模型如图1所示。
1.2 网格划分与边界条件
轴流泵的计算模型由肘形进水流道、叶轮段、导叶段、虹吸式出水流道组成。利用三维实体造型软件PTC Creo Parametric 3.0和前处理软件ICEM建构模型泵装置的三维计算模型及网格剖分,将三维实体导入ICEM CFD中,采用分区非结构化网格剖分,经检查网格质量良好,符合数值模拟要求。计算网格如图2所示。
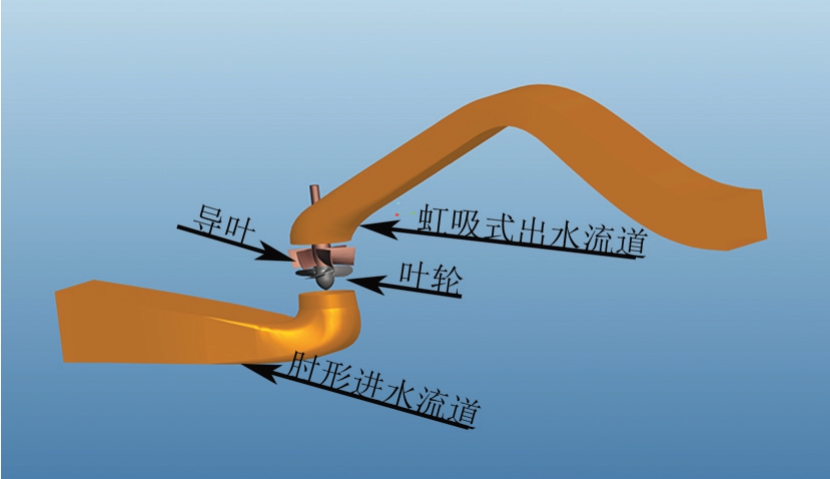
图1 模型泵装置三维透视图
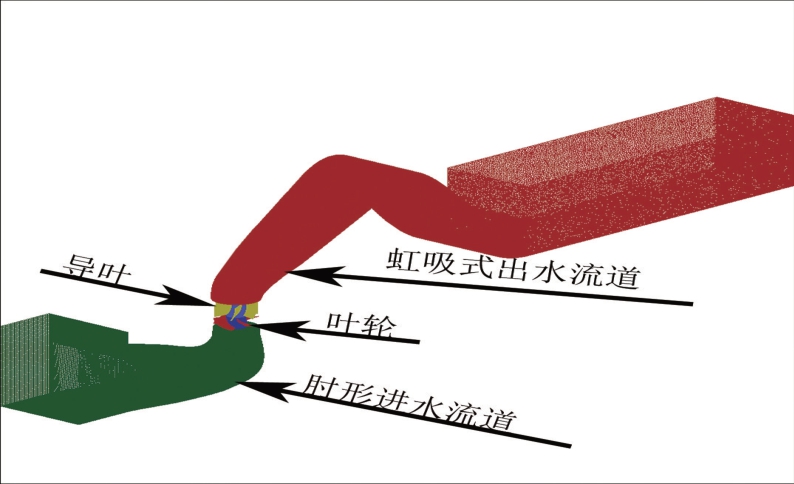
图2 泵装置计算网格
计算中边界条件的设置划分为静止区域与旋转区域,轴流泵的叶轮段设置为旋转区域,其他区域为静止区域,叶轮与静止交界面通过滑移交界面进行连接,采用固定于旋转叶轮上的相对参考坐标,其余交界面均采用None交界面类型。进口为质量进口,设计流量工况下,进口边界条件为300 kg/s,出口为自由出口,参考压力为1个大气压。在进行非定常计算时,取总时间步长为0.276 923 076 s,即叶轮旋转6周所用时间,每个时间步长取0.000 6410 3 s,即每转内经历72步。残差收敛精度设置为10-5。
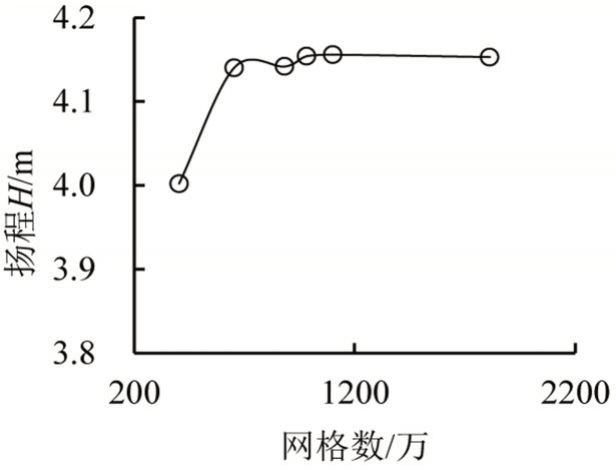
图3 计算网格下的扬程对比
1.3 网格无关性检查
针对研究模型,对设计流量工况下的扬程进行了无关性检验。采用相同的网格拓扑结构,通过改变网格节点数目来调节网格数量,并且保持网格质量不变,通常网格越密集,计算结果越精确。分别采用相同控制方程和边界条件以控制网格数量的单一变量,获得扬程随网格数量变化的曲线,如图3所示。由图3可知,当网格较少时,随着网格数量的增加,轴流泵扬程变化较为明显,当网格数量达到653.63万左右时,再增加网格数量计算所得的扬程变化很小。符合网格无关性检验要求。综合以上因素,选用1 722.898 9万网格数量进行数值计算。
1.4 转子径向力及压力脉动系数
径向力可以简单地认为是叶轮四周流场对叶轮产生的径向作用力,主要由于叶轮周围流场压力分布的不均匀性引起。轴流泵运行时,由于径向力的存在会使转轴在交变应力作用下偏移轴系方向,致使轴流泵内部流场发生变化,流场的变化又会改变轴流泵转子径向力,影响转子的稳定性和装置的安全性。为了研究径向力分布规律,采用计算流体动力学软件ANSYS CFX对轴流泵内部流场进行非定常计算。基于出口压力法[19]计算转子径向力,总压力选取范围包括叶片和叶轮轮毂,假设每个网格节点上的面积相等,且各网格节点处静压均匀分布,先求解耦合面上每一个节点上受到的作用力,然后通过力的分解合成定理,分别计算在x向和y向的作用力,最后求得总的作用力的大小和方向,计算式[20]为:
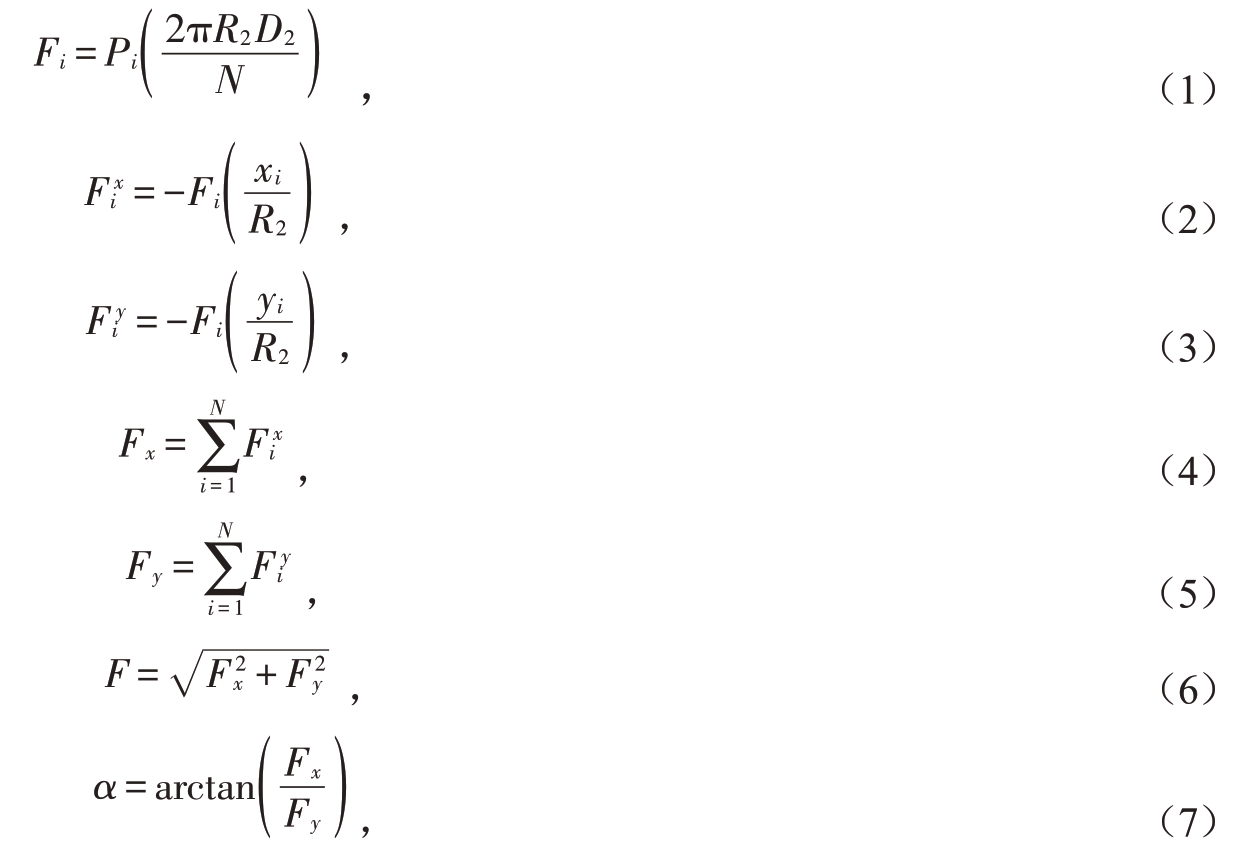
式中:x、y分别为x方向和y方向;R2为叶轮半径;D2为轮缘出口直径;N为耦合面网格节点的个数;Pi为第i个网格节点的压强;Fx为径向力在x轴方向的分量,Fy为径向力在y轴方向的分量;F为径向力的大小;α为径向力与x轴方向的夹角。
通过数值模拟获得压力脉动时域结果,并用压力系数表示压力脉动的状态。压力系数Cp的表达式为:

式中:Δp为监测压力与平均压力之差(Pa);u2为轮缘出口圆周速度(m/s)。
2 外特性试验验证
2.1 试验装置
试验在扬州大学流体动力工程试验室高精度泵站试验台上进行,安装在试验台上的模型试验装置如图4所示。通过江苏省水利厅组织专家鉴定,95%置信频率的泵或泵装置效率系统综合不确定度±0.318%,试验结果真实可靠。在模型泵及泵装置性能试验中,系统通过闸阀和一台辅助泵调节流量,再通过传感器测量水位、扬程、流量、转速、轴功率、汽蚀余量、温度等参数,由NI数据采集卡,配合Labview系统工程软件,实现试验数据实时采样和自动数据处理、显示、打印。

图4 安装在试验台上的泵装置模型照片
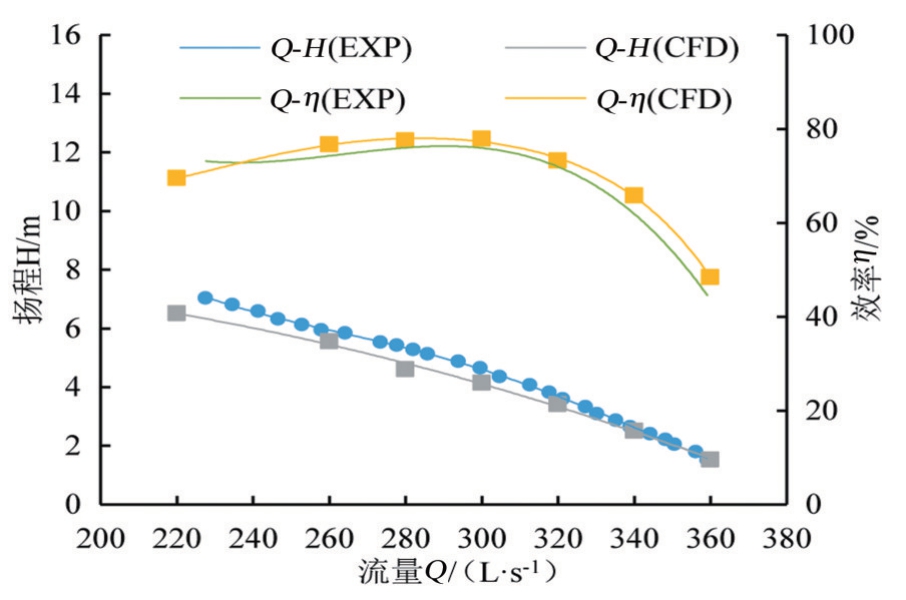
图5 试验与数值计算外特性对比
2.2 外特性验证
通过数值计算获得的外特性结果与试验结果,如图5所示。由图5可知,随着流量的变化,数值计算所得扬程、效率与试验获得的测量结果相差不大,两条曲线基本一致。通过分析流量-扬程曲线发现,小流量工况下,数值计算的流量-扬程曲线与试验测量结果曲线差别较大,这主要是由于小流量工况下靠近马鞍区的流动不稳定引起的;大流量工况下,数值模拟计算结果与试验测量结果基本一致。通过分析流量-效率曲线发现,当流量小于设计工况时,数值计算流量-效率曲线与试验测量结果曲线重合性较好,当流量大于设计工况时,数值计算结果与试验测量结果有所偏差,这主要是由于模拟过程中未考虑各壁面粗糙度所致[18]。总体上讲,各工况下数值计算与试验数据的误差均较小,说明数值计算的准确度较高。
3 结果与分析
3.1 叶轮区域流场分析
通过CFD-POST对数值计算结果进行分析,获得3种流量(0.8Q、1.0Q、1.2Q)的流场分布状态,为更直观地展示叶轮区域流场分布,截取了转子中心平面的压力分布图,如图6所示。由图6可知,转子中心平面压力随着流量的增大而增大;不同流量下转子中心平面压力分布规律基本一致,压力分布关于转动中心均呈现不对称性,存在着压力明显较小区域,当流量从0.8Q变化到1.2Q时,随着内部压力的增大,不对称性逐渐增大,这种现象是由于转子内部流场分布不规律造成的,从而诱发了转子径向力的产生,影响运行的稳定性。
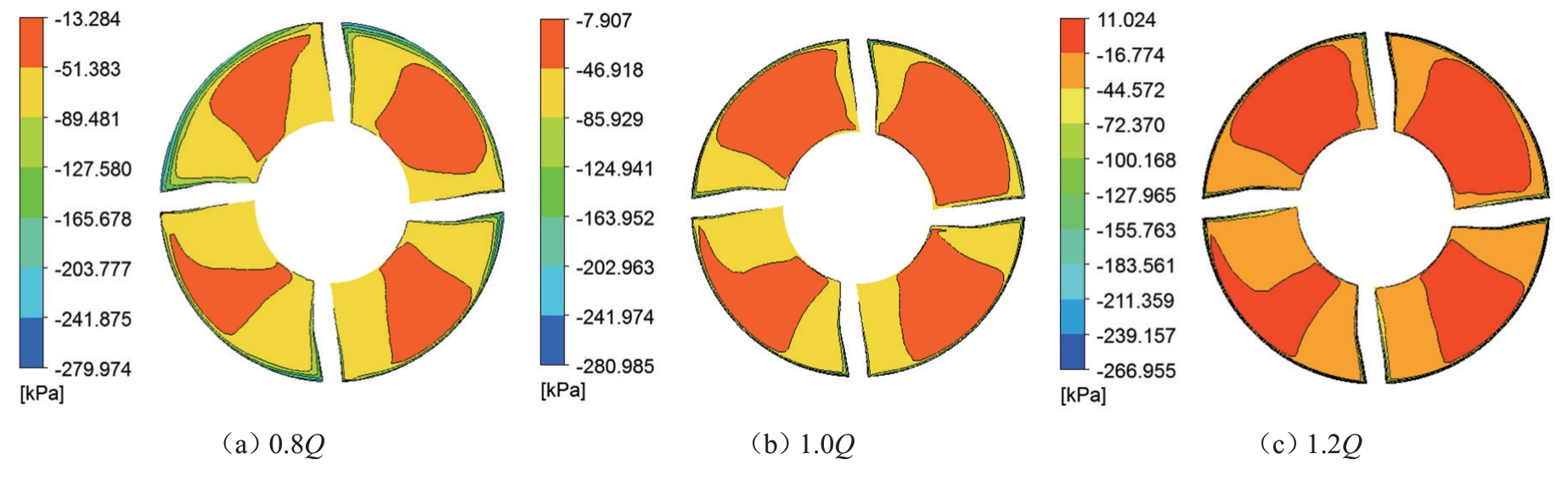
图6 不同工况下转子中心平面压力分布图
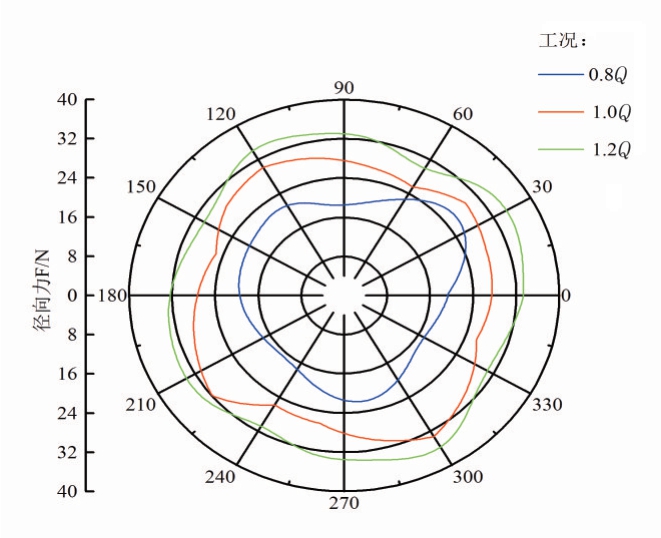
图7 不同工况下转子瞬态径向力轨迹
3.2 转子径向力分析
3.2.1 转子径向力极坐标分布
通过变换得到极坐标下的径向力分布,获得3种不同流量工况下转子旋转一周所受到的瞬态径向力轨迹图,如图7所示。从图7可以看出,3种不同流量工况下径向力的分布基本一致,叶轮旋转1周存在4个周期,与叶片数相同。在0.8Q工况下,轴流泵转子径向力最小,但不同位置径向力波动较大,有着较明显的波峰。在1.0Q工况下,轴流泵转子径向力比在0.8Q工况下大一些,呈现4个明显的波峰和波谷。在1.2Q工况下,轴流泵转子径向力大于其他2个工况,存在4个并不非常明显的周期,波峰和波谷相差较小。
3.2.2 转子径向力时域图
为了进一步分析不同流量工况下转子运行过程中径向力随时间的变化规律,获取了轴流泵转子瞬态径向力合力变化时域图,如图8所示。从图8可以看出,3种流量工况下轴流泵转子瞬态径向力合力均呈周期性波动,存在4个波峰和4个波谷,与叶轮叶片数相同。在不同流量工况下,径向力幅值差异较大,1.0Q工况下径向力呈现出类似正弦函数分布的周期性。1.0Q工况,0.8Q工况下的径向力幅值差异明显,径向力最大幅值为27 N左右,而径向力最小值为17 N左右,由此导致了转子系统的不稳定。而在1.2Q工况下,转子的径向力较大,近似于设计流量工况下径向力的1.5倍,但整体波动幅度较设计流量有所减小。
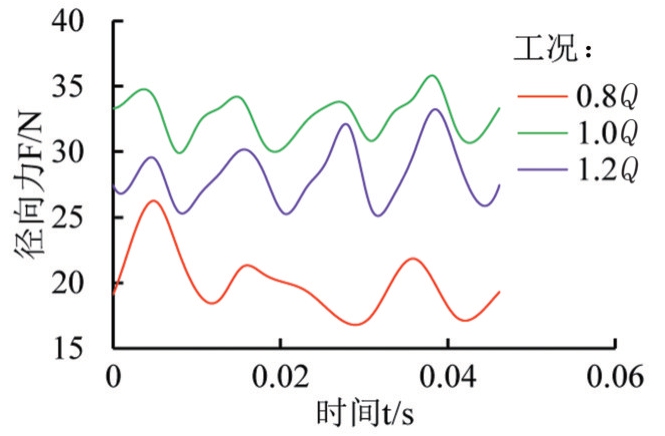
图8 不同工况下瞬态径向力合力变化时域
综上所述,随着流量的增大,水流运动的加剧,轴流泵转子的径向力也随之增大。0.8Q工况下转子的瞬态径向力波动最大,容易引起轴流泵运行不稳定,1.2Q工况下转子瞬态径向力合力波动最小,这是由于0.8Q工况下更加靠近马鞍区,内部流场运动不稳定,致使径向力波动较大,随着流量增大,远离马鞍区,流动较为稳定,径向力波动逐渐减小。
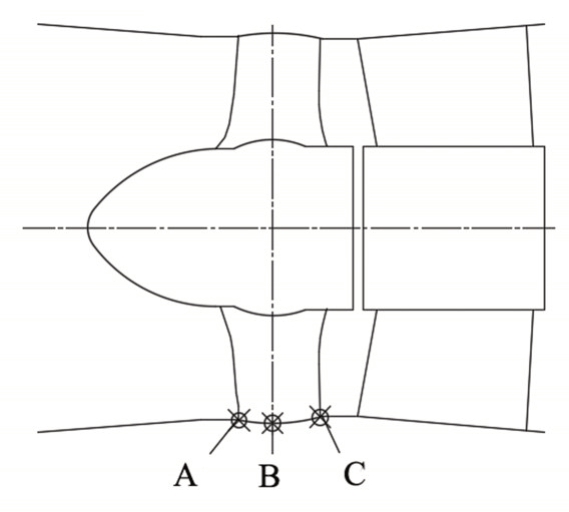
图9 压力监测点位置布置图
3.3 压力脉动结果分析
3.3.1 压力脉动时域分析
在轴流泵轮缘进口、轮缘中间、轮缘出口3个位置分别设置压力脉动的监测点A、监测点B、监测点C,位置分布如图9所示。
获得轴流泵轮缘进口、轮缘中间和轮缘出口3个监测点在0.8Q、1.0Q、1.2Q流量工况下的压力脉动时域图,如图10所示。已知叶轮旋转周期T=0.046 1 s,由图10可知,不同流量工况下各个监测点压力脉动幅值均呈一定的周期性波动,在一个旋转周期内存在这4个明显的波峰和波谷,与叶片数相同。在监测点A和B处,流量1.0Q与0.8Q相比,各点压力脉动的幅值逐渐减小;而在监测点C处,压力脉动系数随流量的变化波动幅度较小,压力脉动较为稳定。
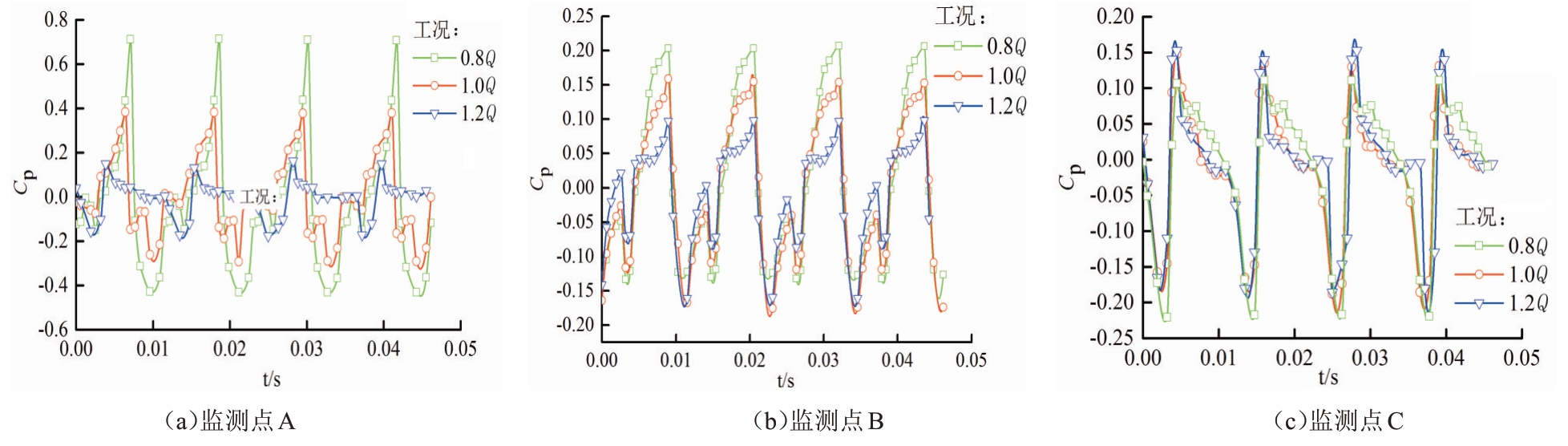
图10 监测点压力脉动时域图
通过上述分析可知,叶轮的旋转周期较大程度影响了各监测点的脉动周期,出现了与叶片数相同的4个波峰和4个波谷。在轮缘进口和轮缘中部位置,压力脉动随流量的变化波动较大,稳定性较差。在轮缘出口的监测点处,压力脉动系数随流量变化变幅较小,说明叶轮出口的压力脉动最稳定。
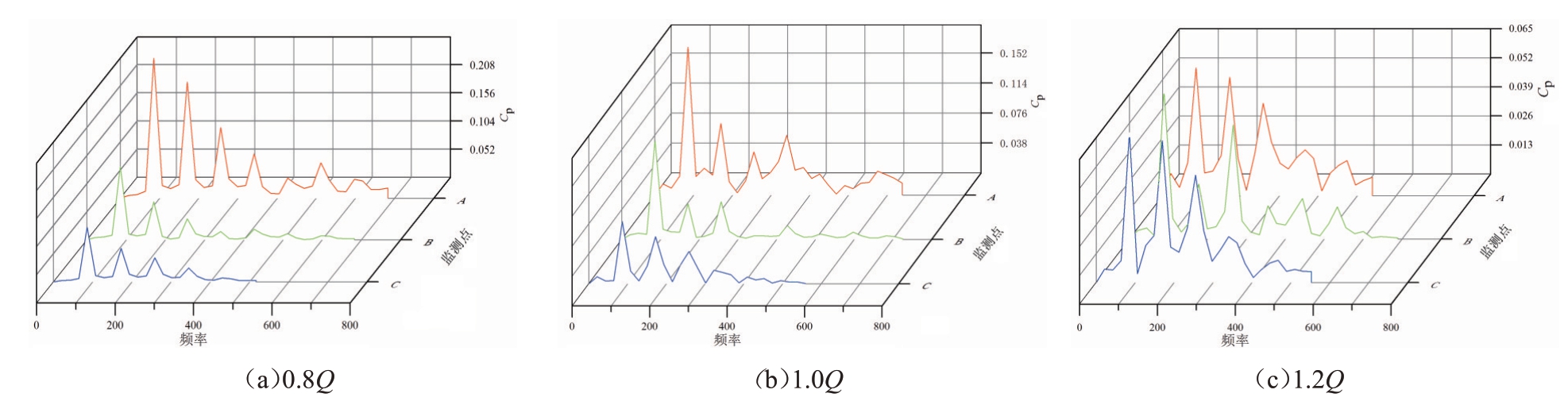
图11 各监测点在不同流量点的压力脉动频域图
3.3.2 压力脉动频域分析
通过快速傅里叶变换得到压力脉动频域图,如图11所示。轴流泵机组的转速是1 300 r/min,则其转动频率f=1 300/60=21.67 Hz,叶片为4片,叶频为频率的4倍,约88 Hz。由图11可知,不同监测点在不同流量工况下的压力脉动的主频出现在88 Hz左右,与叶频相同,而次主频为180 Hz左右,即叶频的二倍频,表明叶片频率始终占主导作用。随着频率的增加,压力系数幅值逐渐减小,表明低频信号更容易诱导压力脉动的产生。通过对比压力系数幅值可知,在0.8Q工况时,轮缘进口监测点处的压力系数最大,随着监测点远离轮缘进口位置,压力系数幅值均渐减小。同时,各监测点压力系数幅值随着流量的增大而逐渐减小,但轮缘进口处压力脉动系数变化较快,轮缘出口处压力脉动系数变化较慢,在1.2Q工况时,各监测点的压力系数幅值逐渐趋近于一致,说明轮缘进口压力系数受流量变化影响最大。综上所述,叶频占压力脉动的主导频率,低频信号是引起压力脉动的主导因素,轮缘进口位置对流量变化较为敏感。
3.3.3 压力脉动峰峰值和主频分析
压力脉动的峰值反映了监测点在旋转周期内所能达到的最高压力。图12为各监测点在不同流量工况下的压力脉动峰峰值。由图12可知,监测点A处的峰值随流量工况的变化较为明显,随着流量的增大,压力脉动峰峰值明显减小。在轮缘进口监测点A处,各流量工况压力脉动的峰峰值均较大,从小流量到大流量变化过程中,压力脉动峰峰值变化较大。在监测点B和监测点C位置处,压力脉动系数随着流量的变化波动较小,其峰值逐渐趋于稳定,压力脉动的峰值基本在0.3附近变化。
压力脉动的主频幅值不仅能够清晰地反映不同流量工况下各个监测点的主频值,而且能够监测不同监测点处的压力脉动系数随流量工况的变化情况。图13为各监测点在不同工况下主频处的压力脉动频域幅值分布情况。由图13可知,监测点A处的压力脉动的主频幅值对流量变化最为敏感,随流量的增大而大幅减小,而监测点C处随流量变化较小。但从整体来看,各监测点的压力脉动主频幅值均随流量的增大而减小。
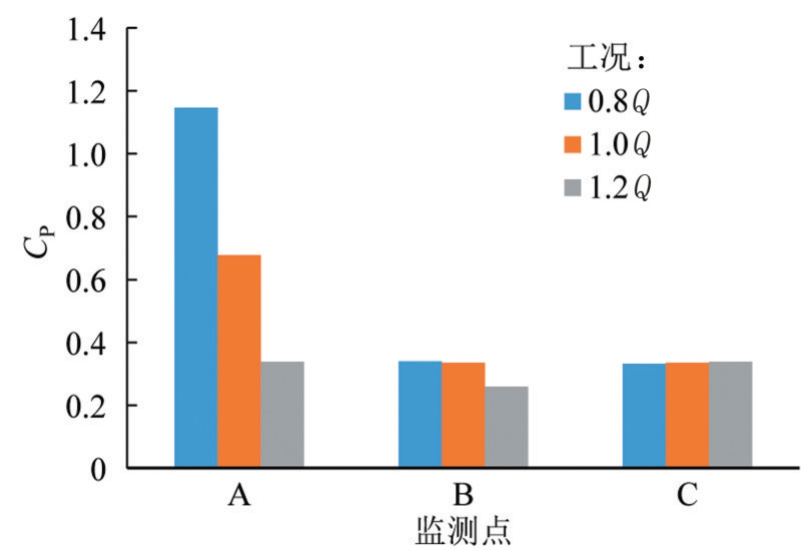
图12 不同工况下监测点压力脉动峰峰值
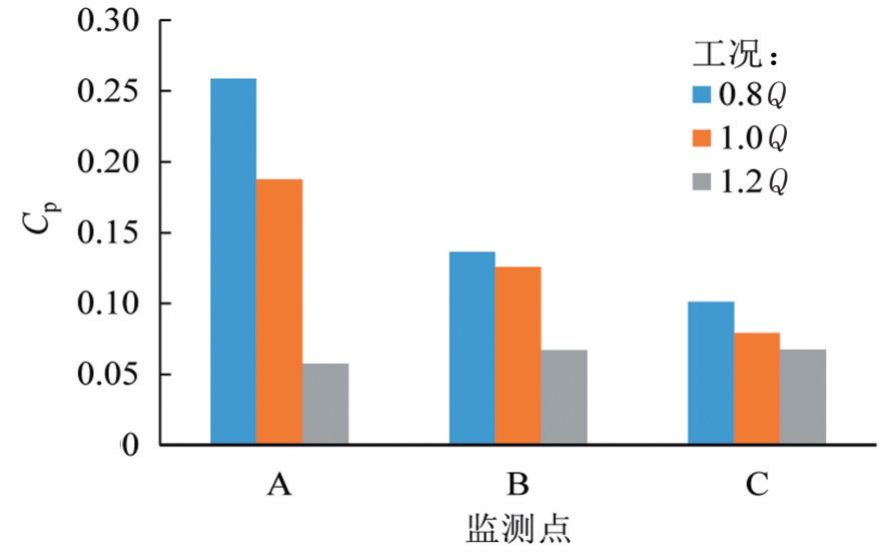
图13 不同工况下监测点压力脉动主频幅值
4 讨论
目前,国内外关于转子径向力方面的研究多集中在离心泵和混流泵方面,而关于轴流泵转子径向力的研究较少,本研究采用定常计算的方法,得知轴流泵转子内部流场分布的不均匀性是造成转子径向力的原因之一。同时对轴流泵内部流场进行非定常计算,获取了轴流泵转子转动一周其径向力的变化特性。研究表明,在一个旋转周期内,轴流泵转子径向力受叶片数影响,存在着与叶片数相同数量的波峰和波谷,转子径向力大小随着流量的增大而增大,径向力波动但却逐渐趋于稳定,这与张琳等[13]研究结果相符。其原因是小流量工况下靠近轴流泵马鞍区,内部流动较不稳定,而随着流量增大,轴流泵内部逐渐趋于稳定,径向力也随之趋于稳定。
为进一步探究轴流泵内部流场分布的规律,分别研究轮缘进口、轮缘中部和轮缘出口3个位置的压力脉动情况。研究表明,叶频对压力脉动占主导作用,叶频为主要频率,这与张德胜等[21]和赵浩儒等[22]的研究结果一致。本研究还表明,随流量的变化,压力脉动随流量的增大而减小,在流量较小时,轴流泵内部压力脉动较大。但轮缘进口压力脉动变化幅度较大,而轮缘中部和轮缘出口相对较小,这说明轮缘进口位置对流量变化较为敏感。
5 结论
1)数值计算的外特性结果与试验测量结果的趋势基本一致,数值计算的准确度较高。
2)转子运动时,内部流场关于转动中心呈现不对称性,这种现象引起转子径向力的产生,造成运行的不稳定性。
3)转子径向力随着流量的增大而增大,1.2Q径向力1.0Q的1.5倍;3种不同流量工况下径向力的分布基本一致,均呈现一定的周期性,小流量工况下较靠近马鞍区,这时转子所受瞬态径向力合力最不稳定,此种现象容易造成转子运行不稳定,当流量增大而逐渐远离马鞍区,这时瞬态径向力波动逐渐减小,大流量工况下转子所受瞬态径向力合力波动最小。
4)在不同流量工况下,叶片通过频率始终对压力脉动占主导作用,轮缘进口监测点A的压力脉动受流量影响最大,随着流量的增大而减小的幅度极为明显,而轮缘出口监测点C处压力脉动受流量影响最小,随着流量的增大而减小的幅度较小;但从整体来看,各监测点压力脉动随着流量的增大而减小,在小流量(0.8Q)情况下,压力脉动较大。
[1]成立,吴璐璐,刘超.大型轴流泵水力不稳定区研究[J].灌溉排水学报,2010,29(2):102-104.
[2]郑源,刘君,周大庆,等.大型轴流泵装置模型试验的压力脉动[J].排灌机械工程学报,2010,28(1):51-55.
[3]常书平,王永生,魏应三,等.喷水推进器内非定常压力脉动特性[J].江苏大学学报(自然科学版),2012,33(5):522-527.
[4]欧鸣雄,施卫东,贾卫东,等.斜流泵叶轮水力径向力的数值模拟与试验验证[J].农业工程学报,2015,31(9):71-76.
[5]FARGE T Z,JOHNSON M W,MAKSOUD T M A.Tip leakage in a centrifugal impeller[J].Journal of Turbomachinery,1989,111(3):244.
[6]黎义,胡鹏林,李仁年,等.不同叶顶间隙对斜流泵性能影响的数值分析[J].农业工程学报,2014,30(23):86-93.
[7]ADKINS D R,BRENNEN C E.Analyses of hydrodynamic radial forces on centrifugal pump impellers[J].Journal of Fluids Engineering,1988,110(1):20.
[8]BARRIO R,FERNÁNDEZ J,BLANCO E,et al.Estimation of radial load in centrifugal pumps using computational fluid dynamics[J].European Journal of Mechanics-B/fluids,2011,30(3):316-324.
[9]袁寿其,周建佳,袁建平,等.分流叶片对螺旋离心泵径向力的影响[J].农业机械学报,2012,43(9):37-42.
[10]杨敏,闵思明,王福军.双蜗壳泵压力脉动特性及叶轮径向力数值模拟[J].农业机械学报,2009,40(11):83-88.
[11]张亮,李欣.长短叶片叶轮双吸离心泵径向力数值仿真[J].机械设计与制造,2017(6):171-174.
[12]张肖,潘中永,张大庆,等.高比转速混流泵空化工况下径向力分析[J].灌溉排水学报,2016,35(4):71-75.
[13]张琳,施卫东,张德胜,等.潜水轴流泵结构动应力分析[J].排灌机械工程学报,2015,33(12):1 026-1 032.
[14]宋希杰,刘超,罗灿.轴流泵装置进水漩涡对压力脉动的影响[J].农业机械学报,2018,49(2):113-119,81.
[15]何乃昌,谈明高,刘厚林,等.轴流泵马鞍区水力性能与压力脉动测试与分析[J].排灌机械工程学报,2018,36(2):118-123.
[16]姚捷,周建佳,孙莎,等.叶片数对轴流泵压力脉动的影响研究[J].通用机械,2016(3):80-84.
[17]张德胜,耿琳琳,施卫东,等.轴流泵水力模型压力脉动和振动特性试验[J].农业机械学报,2015,46(6):66-72.
[18]朱红耕,鄢必鹏,周济人,壁面粗糙度对轴流泵水力性能影响的研究[J].灌溉排水学报,2006,25(1):85-88.
[19]何东升,武学尧,张仲良,等.改型环形灌注泵的径向力研究[J].西安石油学院学报(自然科学版),2002,17(3):2,50-54.
[20]赵万勇,张亮,雒军.双吸离心泵径向力数值分析[J].排灌机械,2009,27(4):205-209.
[21]张德胜,王海宇,施卫东,等.轴流泵多工况压力脉动特性试验[J].农业机械学报,2014,45(11):139-145.
[22]赵浩儒,杨帆,吴俊欣,等.立式轴流泵装置压力脉动特性的试验[J].流体机械,2017,45(7):12-16,27.