0 引言
悬链线形渠道断面不仅具有在施工、制模中易于计算和控制的优点,还具有防止土基冻胀破坏、抵抗外水压力、受力条件好、输沙率高、过水能力强及抵抗冲刷性能好等优点[1-2]。因此,悬链线形渠道在水利水电和灌溉排水工程中得到越来越广泛的应用。
收缩断面水深是分析泄水建筑物下游的水流衔接形式、消能设计及判定水跃位置的关键和前提[3],在水利水电工程中应用十分广泛。近年来,国内外学者对一些简单过水断面收缩水深的分析计算进行了深入研究,取得了较为丰富的研究成果,例如梯形断面[3-4]、抛物线形断面[5-9]、矩形断面[10]等。但悬链线形断面收缩水深的研究成果相对较少。仅滕凯[11]通过引入无量纲收缩水深参数和中间变量参数,对悬链线形断面收缩水深基本方程进行数学变换,采用局部优化拟合的方法,得到无量纲收缩水深的简化计算公式,但该公式结构较为复杂,且最大相对误差达到2.28%,给实际工程应用带来不便。因此,在前人研究的基础上,引入恰当的无量纲参数,通过数学变换得到悬链线形断面无量纲收缩水深的隐函数方程,引入特殊一元二次方程的概念,并基于特殊一元二次方程的定义,在工程适用范围内,对无量纲收缩水深α和收缩水深与悬链线形断面形状参数之比x的值进行回归分析,得到无量纲收缩水深隐函数方程的替代一元二次方程,可方便得到悬链线形断面收缩水深的直接计算公式,并与现有计算公式进行对比和误差分析,以期得到一个形式简捷、计算精度高和适用范围广的直接计算公式,为工程设计部门提供一定参考。
1 特殊一元二次方程的定义
在生产实践中,人们总是希望能用一个简单的函数关系式来描述事物的变化规律,但是事物的变化规律一般较为复杂,当给出自变量或者因变量之后,函数关系式则可能变为复杂的高次或超越方程,使这些方程在理论上无法直接求解。
例如,对于简单的一元二次方程而言,其表达式为:
式中:b1为二次项系数;c1为一次项系数;d1为常数项。
可用简单的求根公式法得到解析解:

式中:Δ=c12-4b1d1≥0。
对于较复杂情况,即复杂的高次或超越方程,在理论上无法直接求解,但若能将高次或超越方程替换为一元二次方程,则可以利用式(2)进行直接求解,因此,在前人的研究基础上[12],提出以下表达式:
式中:λ、μ和η至少有一项为另外1个变量或2个变量的函数。
相较于式(1)的经典一元二次方程,将式(3)定义为特殊一元二次方程。
2 无量纲收缩水深基本方程的建立
由《水力学》[13]知,渠道收缩水深的基本方程为:

式中:E0为以收缩断面底部为基准面的堰前断面的总水头(m);hc为收缩断面水深(m);Q为过水流量(m3/s);g为重力加速度,一般取g=9.81 m/s2;φ为流速系数;Ac为收缩水深过水断面面积(m2)。
2.1 悬链线形断面几何特征及水力要素
悬链线形渠道过水断面如图1所示。
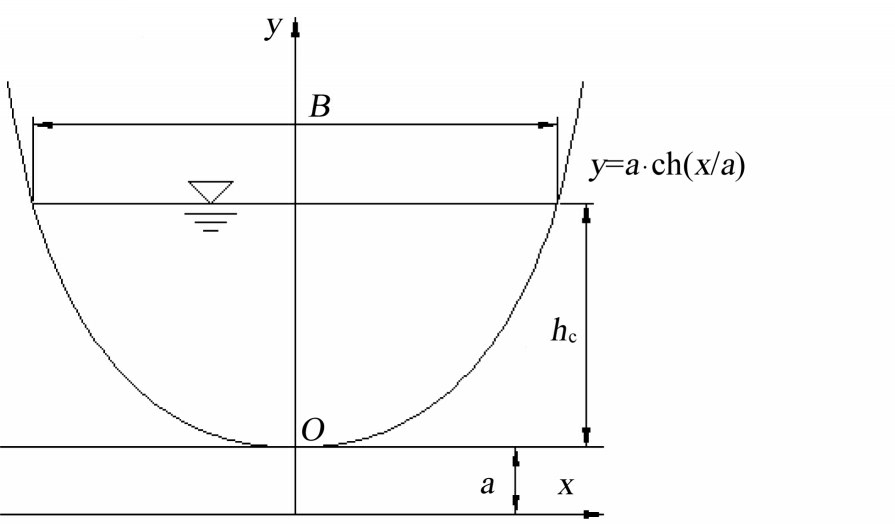
图1 悬链线形渠道过水断面示意图
其过水断面曲线方程为:
设过水断面宽度为B,则过水断面水力要素hc、Ac分别为:

式中:a为悬链线形断面形状参数。
由式(6)可得:
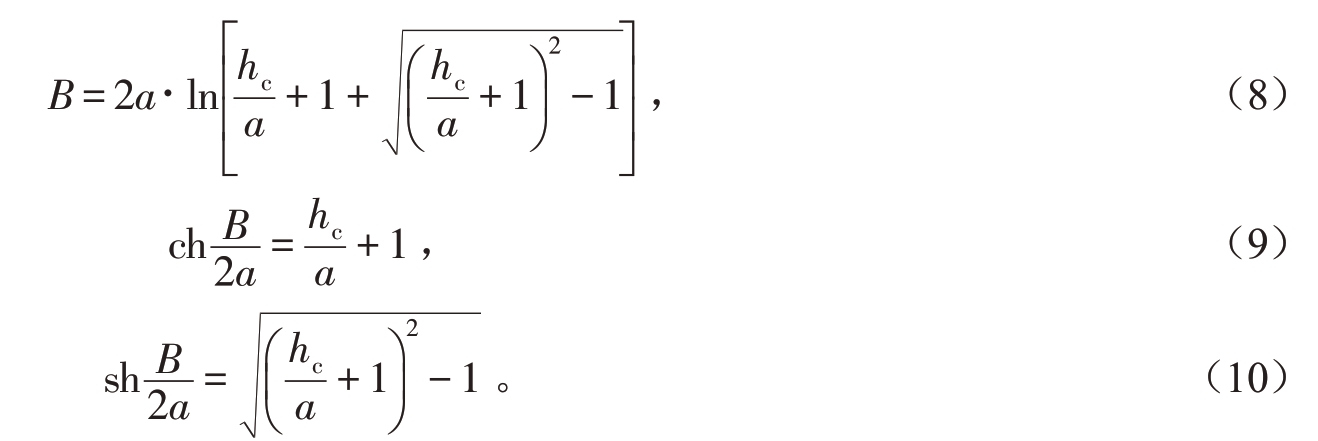
将式(8)、式(9)、式(10)带入式(7)可得:
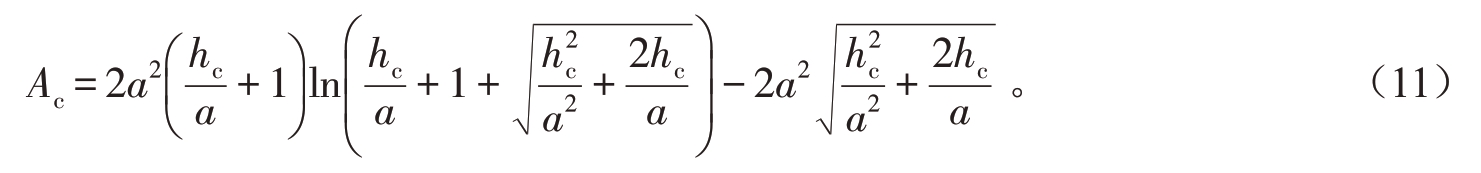
2.2 悬链线形收缩水深的基本计算公式推导
将式(11)带入式(4),并设:
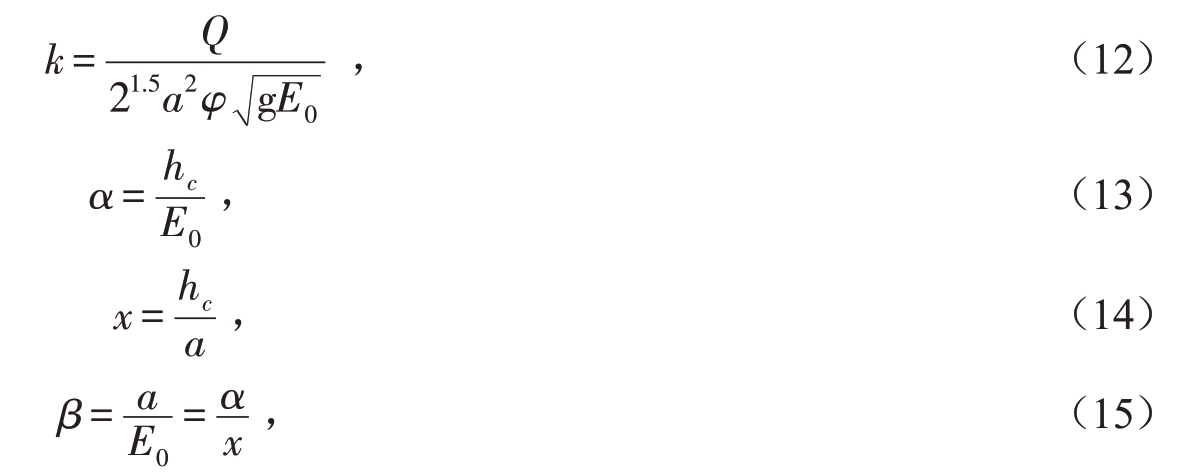
式中:k、β均为无量纲参数;α为无量纲收缩水深;x为收缩水深与悬链线形断面形状参数之比。
则式(4)可整理为:
式(16)为悬链线形断面无量纲收缩水深的基本计算公式,即悬链线形断面无量纲收缩水深的隐函数方程。
在实际工程中,a通常不给定,而是给出设计流量相应正常水深的水面宽度B0和a的比值ε,即B0/a=ε,可由式(17)直接计算断面形状参数a[1]:
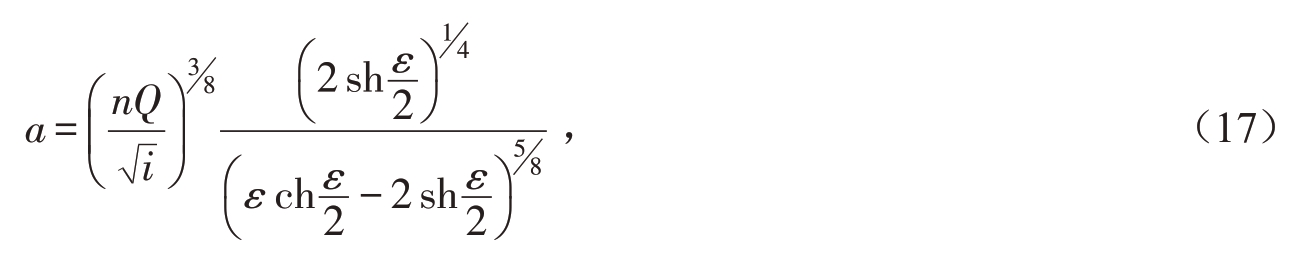
式中:Q为渠道设计流量(m3/s);n为渠道糙率系数;i为渠道设计坡降。
3 悬链线形断面收缩水深的直接计算公式
根据工程实际[14-18],α的取值范围为[0.01,0.5]。在泄流中水深最小、流速最大的断面为收缩水深断面,即在泄流时势能逐渐转化为动能,水深减小,流速增加,当到达收缩水深断面时其水深小于临界水深,即hc<hk,此外,根据文献[19],悬链线形断面无量纲临界水深hk/a的取值范围为[0.537,6.945],因此,可将上述取值范围适当左右延展,即可取x∈[0.5,7]作为本文公式的适用范围。
根据无量纲参数α、β和x的函数关系,基于提出的特殊一元二次方程的定义,对符合条件的函数模型进行数学变换,在α∈[0.01,0.5],x∈[0.5,7]的范围内,对α~x的值进行回归分析,从而得到最佳函数模型,进而得到式(16)的最佳一元二次替代方程,即:
式中:

解一元二次方程式(18),即可得到收缩水深直接计算式:

由式(13)得:
在对α~x进行回归分析时发现,对于确定的α∈[0.01,0.5]取值,在x∈[0.5,7]的范围内,大部分区域内计算值和真值吻合良好,仅在x∈[0.5,2.5]的范围内,计算值和真值偏离较大。因此,为了提高直接计算公式的精度,将x分段取值,分段区间及其所对应的λ、μ和η值见表1。
表1 分段函数参数表

取值范围α∈[0.01,0.5],x∈[0.5,2.5]α∈[0.01,0.5],x∈[2.5,7]λ λ=1-0.655 4 k1.4β2 λ=1-0.560 3 k1.4β2 μ μ=0.403 1-0.003 374 k1.4β μ=0.4301-0.557 2 k1.4β η η=0.745 1-0.010 14 k1.4 η=0.745 1-0.846 4 k1.4
4 公式误差分析及比较
4.1 本文公式误差分析
在工程适用范围内,即α∈[0.01,0.5],x∈[0.5,7],当已知Q、E0、η、φ时,k、β、α可由式(12)、式(15)、式(17)求得,真值α、x可由式(16)相应求得。在进行误差分析时,在α∈[0.01,0.5],x∈[0.5,7]范围内,给出α、x的值,根据式(15)、式(16)、式(22)、式(23),反求无量纲收缩水深和收缩水深,对计算值的误差分析采用相对误差来描述,如图2所示。
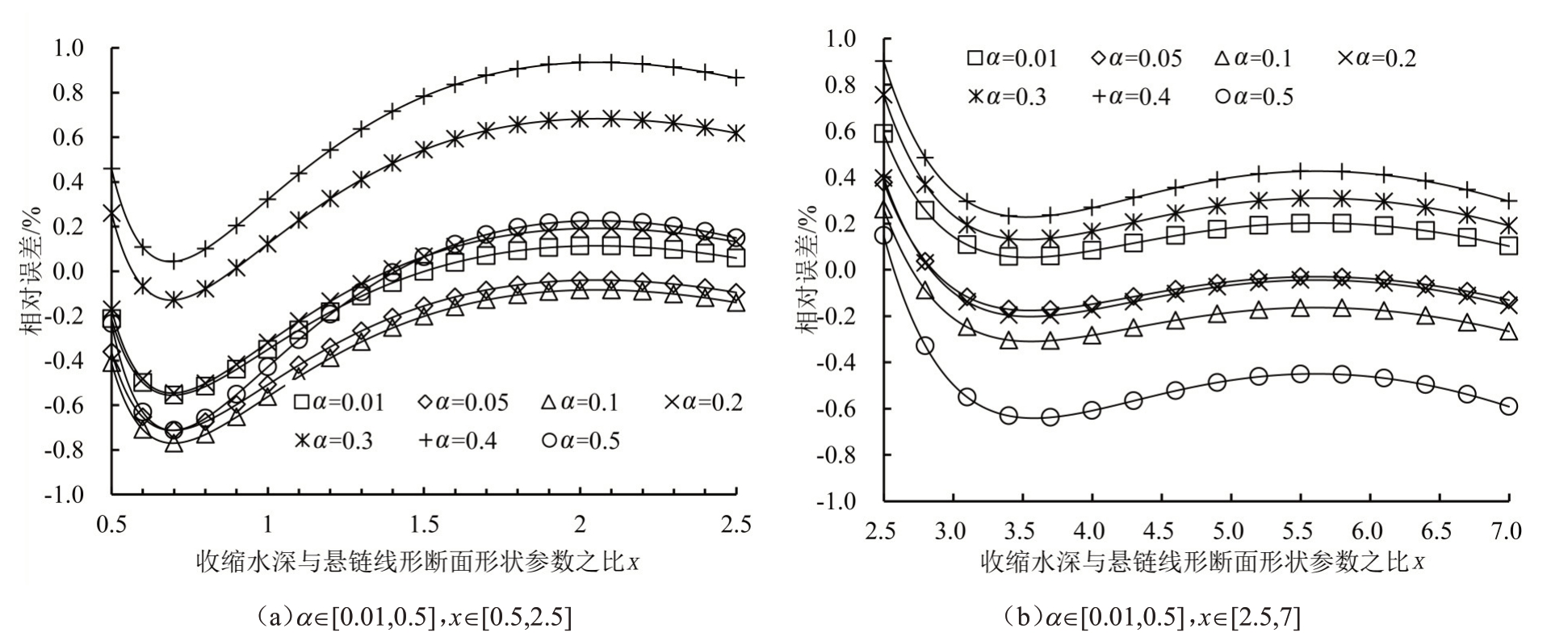
图2 收缩水深误差分布图
由图2(a)可知,在α∈[0.01,0.5],x∈[0.5,2.5]时,收缩水深相对误差绝对值小于0.94%;以α=0.01、0.2、0.5对应的相对误差绝对值较小,其他α值的相对误差绝对值分布曲线位于α=0.01曲线的上下方,对应的相对误差绝对值较大;当α=0.4时,相对误差绝对值最大,但在α∈[0.4,0.5]范围内相对误差绝对值逐渐减小。由图2(b)可见,在α∈[0.01,0.5],x∈[2.5,7]时,收缩水深相对误差绝对值小于0.91%;以α=0.01、0.05、0.2对应的相对误差绝对值最小,其他α值的相对误差绝对值分布曲线位于α=0.01曲线的上下方,对应的相对误差绝对值较大;当α=0.5时,对应的相对误差绝对值最大。由图(2)可知,当点x=2.5时,图2(a)和图2(b)计算误差不相等,但当x属于[2.5,7]时,计算误差较小,因此建议在遇到该计算问题时,选用x∈[2.5,7]的函数形式。
4.2 公式对比分析
对于悬链线形断面收缩水深的计算公式,目前仅有滕凯1个公式[11],即:

式中:k、β、x与前文定义相同。
滕凯公式采用参数x进行误差分析,因参数x与α一一对应,因此,采用参数x分析结果与本文采用参数α分析结果相同。在α∈[0.01,0.5],x∈[0.5,7]时,滕凯公式收缩水深误差分布如图3所示。
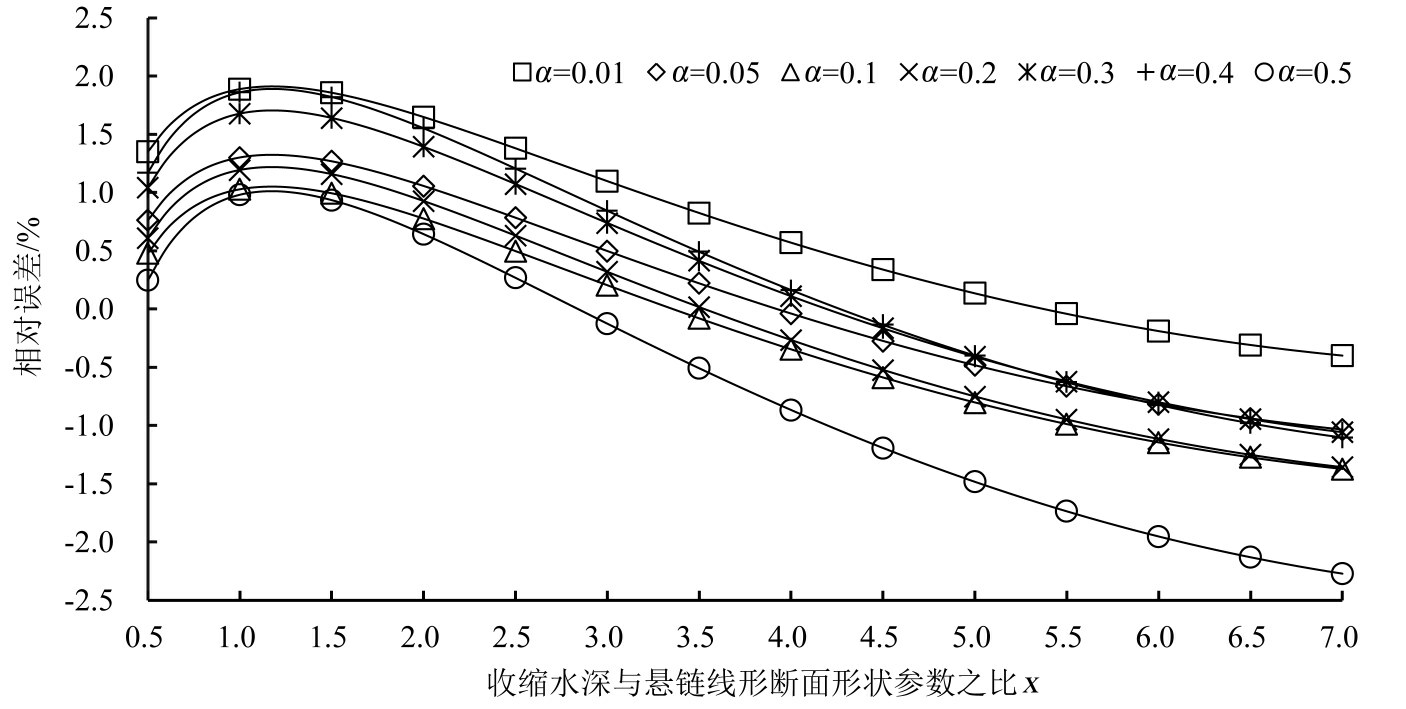
图3 收缩水深误差分布图
由图3可见,在α∈[0.01,0.5],x∈[0.5,7]时,滕凯公式收缩水深相对误差绝对值最大值为2.28%;当α=0.01相对误差绝对值分布曲线位于最上方,其他α的相对误差绝对值分布曲线位于α=0.01曲线的下方,当α=0.5时,对应的相对误差绝对值最大。通过公式对比及误差分析发现,滕凯公式收缩水深直接计算公式相对误差绝对值与本文公式相对误差绝对值(最大值为0.94%)相比明显偏大,且大部分区域误差绝对值大于1%,此外,滕凯公式较为复杂,而式(23)形式为一元二次方程的求根公式,形式简捷,便于工程设计人员使用。
5 应用举例
选用文献[11]的算例:已知水库溢流坝坝前断面总水头E0=10.7 m,坝上设计通过流量Q=140 m3/s,坝后选用悬链线形断面渠道,其断面曲线方程为:
已知流速系数φ=0.95,试求坝下断面收缩水深hc值。
1)由已知量Q、E0、a、φ,根据式(12)、(15)求k、β的值,可得(若已知ε值,可由式(17)直接计算a值):![]()
2)选用α∈[0.01,0.5],x∈[2.5,7]区间所对应的函数形式,将k、β的值带入式(19)—式(21),得:
3)将λ、μ和η的值带入式(23),得![]()
经验证hc/a=6.2079∈[2.5,7],则公式选择正确,hc为所求值。
由文献[11]知,本算例精确解为hc2=4.64 m,本文直接计算公式的计算相对误差为0.34%,滕凯公式计算相对误差为1.08%,可见本文公式精度较高,满足工程计算精度要求。
6 结论
通过选择恰当的无量纲参数,由悬链线形断面收缩水深基本方程得到其无量纲收缩水深的隐函数方程,引入特殊一元二次方程的概念,在α∈[0.01,0.5],x∈[0.5,7]范围内,根据特殊一元二次方程的定义,对α~x的值进行回归分析,得到无量纲收缩水深隐函数方程的替代一元二次方程,求解即可得到悬链线形断面收缩水深的直接计算公式,通过对公式误差分析比较,在工程适用范围内,直接公式计算值最大相对误差绝对值小于0.94%,明显低于现有计算公式的结果(2.28%),且新提出的计算公式形式简捷、适用范围广,可为工程实际应用提供便利。
[1]冯雪,马子普.悬链线形渠道正常水深与临界水深的计算方法[J].水电能源科学,2012,30(11):88-90.
[2]吕宏兴,冯家涛.明渠水力最佳断面的比较[J].人民长江,1994,25(11):42-45.
[3]赵延风,王正中,芦琴.梯形断面收缩水深的直接计算公式[J].农业工程学报,2009,25(8):24-27.
[4]王正中,雷天朝,宋松柏,等.梯形断面收缩水深计算的迭代法[J].长江科学院院报,1997,14(3):15-17.
[5]王正中,王羿,赵延风,等.抛物线断面河渠收缩水深的直接计算公式[J].武汉大学学报(工学版),2011,44(2):175-177,191.
[6]文辉,李风玲.抛物线形断面渠道收缩水深的解析解[J].长江科学院院报,2009,26(9):32-34.
[7]赵延风,宋松柏,孟秦倩.抛物线形断面渠道收缩水深的直接计算方法[J].水利水电技术,2008,39(3):36-37,41.
[8]滕凯.抛物线形断面渠道收缩水深简化计算通式[J].水利水电科技进展,2014,34(3):61-64.
[9]芦琴,王正中,任武刚.抛物线形渠道收缩水深简捷计算公式[J].干旱地区农业研究,2007,25(2):134-136.
[10]赵延风,王正中,孟秦倩.矩形断面收缩水深的直接计算方法[J].人民长江,2008,39(8):102-103.
[11]滕凯.悬链线形断面渠道收缩水深的简化算法[J].西北水电,2013(1):19-21.
[12]赵延风,宋松柏,孟秦倩.城门洞形断面收缩水深的近似计算公式[J].节水灌溉,2007(8):22-23.
[13]孙东坡,丁新求.水力学[M].郑州:黄河水利出版社,2013:260-263.
[14]赵延风,王正中,孟秦倩.无压流圆形断面收缩水深的近似计算公式[J].三峡大学学报(自然科学版),2009,31(1):6-8.
[15]冷畅俭,王正中.三次抛物线形渠道断面收缩水深的计算公式[J].长江科学院院报,2011,28(4):29-31,35.
[16]谢成玉,滕凯.三次抛物线形渠道断面收缩水深的简化计算公式[J].南水北调与水利科技,2012,10(1):136-138.
[17]赵延风,王正中,刘计良.抛物线类渠道断面收缩水深的计算通式[J].水力发电学报,2013,32(1):126-131.
[18]陈诚,龚懿,王洁,等.立方抛物线形断面收缩水深的直接计算研究[J].中国农村水利水电,2017(2):173-175,181.
[19]陈诚,龚懿,王洁,等.悬链线形断面渠道临界水深的直接计算方法[J].灌溉排水学报,2016,35(11):29-33.